Kezdőlap


Feladat:	354. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balázs Béla , Durst E. , Havas J. , Kántor S. , Németh Gy. , Pataki K. , Peregi F. , Szabó J. , Veszprémi áll. ált.g. mat. szakköre , Villányi O. , Zobor E.
Füzet:	1952/február, 19 - 20. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Terület, felszín, Geometriai egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1951/november: 354. matematika feladat

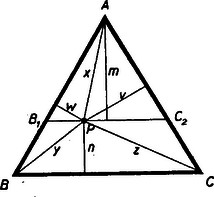
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $P$ ponton át húzzunk a $B C$ oldallal párhuzamost, messe ez a másik két oldalt $B_{1}$ , ill. $C_{1}$ pontokban.^{$^{*}$}

A B_{1} C_{1}

egyenlőoldalú háromszög oldalát jelöljük

a

-val és húzzuk meg ebben a háromszögben az

A

csúcsponthoz tartozó magasságot,

m

-et. E háromszög kétszeres területe nyilván

\begin{matrix} a m = a v + a w = a (v + w), \end{matrix}

vagyis

\begin{matrix} m = v + w . \end{matrix}

m

befogója egy olyan derékszögű háromszögnek, melynek átfogója

x

, tehát

x \geq m

. (Az egyenlőség csak akkor áll fenn, ha

P

m

talppontja.)
Mivel

m = v + w

, azért

x \geq v + w

. Természetesen ugyanígy kimutatható

y \geq u + w

, és

z \geq u + v

. E három egyenlőtlenség összeadásából következik

\begin{matrix} x + y + z \geq 2 (u + v + w), \end{matrix}

ami bizonyítandó volt.
Az ,,='' jel csak akkor érvényes, ha

P

mindhárom esetben

m

talppontja, vagyis

P

a háromszög súlypontja. Ez esetben fennállanak az

x = 2 u

y = 2 v

és

z = 2 w

egyenlőségek.

Balázs Béla

^{$^{*}$}Az ábrában

C_{2}

és

n

sajtóhiba,

C_{1}

és

u

helyett.