Kezdőlap


Feladat:	334. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	ifj. Csonka Pál , Kántor S.
Füzet:	1951/december, 236. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Egyéb sokszögek geometriája, Szélsőérték-feladatok differenciálszámítás nélkül, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1951/augusztus: 334. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Állapítsuk meg, hogy a sokszög $a$ és $b$ oldala két szomszédos osztáspontjának összekötővonala által lemetszett háromszög területe, mely $λ$ értéknél a legnagyobb!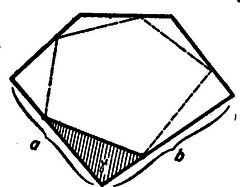

Egy ilyen háromszög területe:

\begin{matrix} t = \frac{(a - λ a) \cdot λ b \cdot sin γ}{2} = (1 - λ) \cdot λ \frac{a b sin γ}{2} . \end{matrix}

Ilyen kifejezések összegét kell vizsgálnunk.
Minthogy az

\frac{a b \cdot sin γ}{2}

kifejezések összege állandó, elégséges azt megtudni, hogy az

y = (1 - λ) λ = - λ^{2} + λ

kifejezés milyen

λ

értéknél maximális. Ez a függvény

λ

y

koordinátarendszerben, az

y

tengellyel párhuzamos tengelyű parabolával ábrázolható. Ez a parabola a

λ = 1

, és

λ = 0

helyeken metszi a

λ

tengelyt,

λ

legnagyobb értéke tehát a

λ = 0, 5

helyen van.

ifj. Csonka Pál (Budapest, III. o.)

Megjegyzés. 1

^{\circ}

. A maximum helye tisztán algebrailag így adódik:

y = \frac{1}{4} - {(1 - \frac{1}{2})}^{2}

maximumát,

\frac{1}{4}

-et ott veszi fel, ahol e négyzet értéke

0

, vagyis

a = \frac{1}{2}

.
2

^{\circ}

. Az állítás nem igaz horpadt sokszögekre, mert ott a számításban szereplő háromszögek egy része csökkenést, másik része növekedést jelent az adott sokszög területéhez képest. Így a

λ (λ - 1)

szorzat növekedésével lehet, hogy nő, de az is lehet, hogy csökken az új sokszög területe. Ha pedig pl. egy négyzet csúcsaiba

45^{\circ}

-os szögeket helyezünk el úgy, hogy az átlók legyenek a szögfelezőik, akkor olyan csillag-négyszöget kapunk, amelyről a fenti módon készített sokszögek mind egyenlő területűek.