Kezdőlap


Feladat:	312. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1951/november, 115 - 116. oldal		PDF \| MathML
Témakör(ök):	Jensen-féle egyenlőtlenség, Feladat
Hivatkozás(ok):	Feladatok: 1951/augusztus: 312. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Írjuk fel pl. az $\frac{1}{x}$ görbére, hogy minden olyan húr középpontja, melynek végpontjai pozitív abszcisszájúak, a görbe fölött van. Legyen $a$ és $b$ pozitív

\begin{matrix} \frac{\frac{1}{a} + \frac{1}{b}}{2} \geq \frac{1}{\frac{a + b}{2}}, azaz \frac{a + b}{2} \geq \frac{1}{\frac{\frac{1}{a} + \frac{1}{b}}{2}} = \frac{2 a b}{a + b} . \end{matrix}

A geometriai szemlélet tehát közvetlenül adta, hogy a számtani közép nagyobb a harmonikusnál. Sok egyéb érdekes és fontos egyenlőtlenséget írhatnánk még fel megállapításaink alapján, a baj csak az, hogy nem építünk biztos alapokra, mikor szemléletünkre bízzuk annak eldöntését, hogy egy függvény hol konvex, hol konkáv.
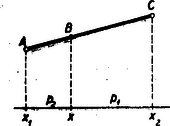
Eldönthetjük ezt a szemlélet igénybevétele nélkül is, éppen azt a tulajdonságot fejezve ki az algebra nyelvén, ami a konvex görbéket jellemzi, hogy a húr mindig a görbe fölött van. Legyen

x

az (

x_{1}, x_{2}

) szakasz egy belső pontja az

X

-tengelyen. Először is

x

-et szeretnénk

x_{1}

és

x_{2}

segítségével írni fel.

\begin{matrix} x = x_{1} + \frac{x - x_{1}}{x_{2} - x_{1}} (x_{2} - x_{1}) = \frac{x_{2} - x}{x_{2} - x_{1}} x_{1} + \frac{x - x_{1}}{x_{2} - x_{1}} x_{2} . \end{matrix}

x_{2} - x = p_{1}

x - x_{1} = p_{2}

jelölést használva

x_{2} - x_{1} = p_{1} + p_{2}

x

a távolságot

p_{2} : p_{1}

arányban osztó pont. Abszcisszájára:

\begin{matrix} x = \frac{p_{1} x_{1} + p_{2} x_{2}}{p_{1} + p_{2}} . \end{matrix}

x

az (

x_{1}, x_{1}

) szakasz belső pontja (és csakis ekkor)

p_{1}

és

p_{2}

pozitív. Ha

\frac{p_{1}}{p_{1} + p_{2}}

és

\frac{p_{2}}{p_{1} + p_{2}}

helyett

q_{1}

és

q_{2}

-t írunk, akkor

\begin{matrix} x = q_{1} x_{1} + q_{2} x_{2}, ahol q_{1}, q_{2} pozitív és q_{1} + q_{2} = 1. \end{matrix}

Írjuk fel most az

x_{1}

és

x_{2}

abszcisszájú pontok közti húr

x

abszcisszájú

B

pontjának ordinátáját. (Feltesszük a továbbiakban mindig, hogy

x_{1} \neq x_{2}

.) Jelöljük ezt

y

-nal. Az ábráról látható, hogy

\begin{matrix} \frac{y - f (x_{1})}{f (x_{2}) - y} = \frac{A B}{B C} = \frac{p_{2}}{p_{1}} = \frac{q_{2}}{q_{1}} . \end{matrix}

Innen egyszerű átalakítással nyerjük, hogy

\begin{matrix} y = \frac{p_{1} f (x_{1}) + p_{2} f (x_{2})}{p_{1} + p_{2}} = \frac{q_{1} f (x_{1}) + q_{2} f (x_{2})}{q_{1} + q_{2}} = q_{1} f (x_{1}) + q_{2} f (x_{2}) . \end{matrix}

A mondott geometriai tulajdonságot tehát így írhatjuk algebrai formában:

f (x)

akkor és csakis akkor konvex, ha minden

x_{1}

x_{2}

számhoz és bármely 0-tól különböző pozitív

p_{1}

és

p_{2}

számokra (úgynevezett súlyokra)

\begin{matrix} f (\frac{p_{1} x_{1} + p_{2} x_{2}}{p_{1} + p_{2}}) < \frac{p_{1} f (x_{1}) + p_{2} f (x_{2})}{p_{1} + p_{2}} . \end{matrix}

(1)

Írhatjuk az egyenlőtlenséget így is: bármely pozitív

q_{1}

és

q_{2}

súlyokra, melyekre

q_{1} + q_{2} = 1

\begin{matrix} f (q_{1} x_{1} + q_{2} x_{2}) < q_{1} f (x_{1}) + q_{2} f (x_{2}) . \end{matrix}

'

)

A nyert egyenlőtlenséget nevezik: súlyozott Jensen‐féle egyenlőtlenségnek. Ez fejezi ki tehát azt, hogy a függvény konvex. Ha

q_{1} = q_{2} = \frac{1}{2}

, akkor kapjuk a szimmetrikus Jensen-egyenlőtlenséget.

\begin{matrix} f (\frac{x_{1} + x_{2}}{2}) < \frac{f (x_{1}) + f (x_{2})}{2} . \end{matrix}

(2)