Kezdőlap


Feladat:	306. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Kántor Sándor
Füzet:	1951/november, 159 - 160. oldal		PDF \| MathML
Témakör(ök):	Térfogat, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1951/május: 306. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszuk ki a három leghosszabb testmagasságot: $m_{1}$ , $m_{2}$ , $m_{3}$ . Legyen ezek talppontja rendre: $M_{1}$ , $M_{2}$ , $M_{3}$ . Fordítsuk úgy a tetraédert, hogy az alaphoz $m_{1}$ magasság tartozzon. Az $M_{2}$ és $M_{3}$ pontok a tetraéder egy‐egy oldallapján vannak. Ezek közül az egyik, pl. az $M_{2}$ -n átmenő oldallapon fekvő alapélt jelöljük $a$ -val, az alaplap $a$ -hoz tartozó magasságát $m$ -mel, ekkor $a m m_{1}$ a tetraeder hatszoros köbtartalma.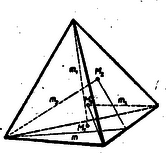

Kössük össze

m

és

a

egyenesek metszéspontját az

M_{2}

ponttal, ezáltal oly derékszögű háromszög keletkezik, melynek átfogója

m

, egyik befogója

m_{2}

, eszerint

m \geq m_{2}

. Az

m_{3}

magasság az

a

él egyik végpontjából indul ki. Kössük össze az él másik végpontját is az

M_{3}

ponttal, ezáltal oly derékszögű háromszög keletkezik, melynek átfogója

a

, egyik befogója

m_{3}

, eszerint

a \geq m_{3}

. E két egyenlőtlenség figyelembevételével

\begin{matrix} a m m_{1} \geq m_{1} m_{2} m_{3} . \end{matrix}

tehát a tetraéder hatszoros térfogata nagyobb vagy legfeljebb egyenlő a három legnagyobb testmagasság szorzatával.
Az egyenlőség akkor és csakis akkor következik be, ha mind a két derékszög egyenessé fajul, ekkor

m

egybeesik

m_{2}

-vel,

a

pedig

m_{3}

-mal. Ilyen a tetraéder, ha három lapja páronként merőleges egymásra, tehát derékszögű csúcsa van.

Kántor Sándor