Kezdőlap


Feladat:	300. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barabás Gy. , Kántor S. , Zobor Ervin
Füzet:	1951/november, 153. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Hozzáírt körök, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1951/május: 300. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $O$ az $A B C$ háromszöget belülről érintő és $O_{a}$ az $a$ oldalhoz írt kör középpontja.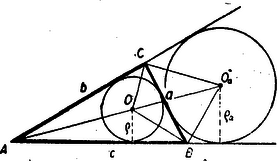

Fejezzük ki

ϱ

ϱ_{a}

ϱ_{b}

és

ϱ_{c}

értékét

t

segítségével. Az

A B C

háromszög területe az

A B O

B C O

és

C A O

területéből tevődik össze, tehát

\begin{matrix} t = \frac{c ϱ}{2} + \frac{a ϱ}{2} + \frac{b ϱ}{2} = ϱ \frac{a + b + c}{2} = ϱ s, \end{matrix}

ahol

s

a háromszög fél kerülete:

s = \frac{a + b + c}{2}

. Eszerint

ϱ = \frac{t}{s}

Kössük össze a háromszöghöz írt körök középpontjait is a háromszög csúcsaival, pl. az

O_{a}

pontot. Így ismét három olyan háromszöget nyerünk, melyek kiadják a háromszög területét, ha a

B C O

háromszögét, mely a

B C

oldal külső partján fekszik, a másik két háromszög területének összegéből levonjuk. (

B C

oldal belső partján értjük az oldallal kettévágott síknak azt a felét, amelyen az

A B C

háromszög fekszik, a sík másik fele az oldal külső partja.) Eszerint

\begin{matrix} t = t_{A B O_{a}} - t_{B C O_{a}} + t_{C A O_{a}} = \frac{c ϱ_{a}}{2} - \frac{a ϱ_{a}}{2} + \frac{b ϱ_{a}}{2} = \\ = ϱ_{a} \frac{b + c - a}{2} = ϱ_{a} (s - a) . \end{matrix}

Innen

ϱ_{a} = \frac{t}{s - a}

. Hasonlóan nyerhetjük, hogy

ϱ_{b} = \frac{t}{s - b}

ϱ_{c} = \frac{t}{s - c}

, és egyenleteink összeszorzásával

\begin{matrix} ϱ ϱ_{a} ϱ_{b} ϱ_{c} = \frac{t^{4}}{s (s - a) (s - b) (s - c)} . \end{matrix}

Ámde Heron képlete szerint

\begin{matrix} s (s - a) (s - b) (s - c) = t^{2} és így ϱ ϱ_{a} ϱ_{b} ϱ_{c} = t^{2} . \end{matrix}

Zobor Ervin

Megoldotta: Barabás Gy., Kántor S.