Kezdőlap


Feladat:	299. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kántor S. , Rédly E. , Zobor E.
Füzet:	1951/november, 152. oldal		PDF \| MathML
Témakör(ök):	Középponti és kerületi szögek, Síkgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1951/május: 299. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a $k_{1}$ körön tetszőlegesen választott pont $A$ , a $k_{1}$ és $k_{2}$ kör két metszéspontja $D$ és $E$ . Az $A D$ egyenes metszése a $k_{2}$ körrel $B$ , az $A E$ egyenesé $C$ . Az $A B C$ háromszög szögei 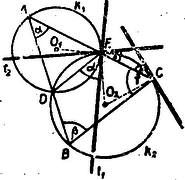$α$ , $β$ és $γ$ .

t_{1}

érintő és a

D E

húr szöge egyenlő az

α

szöggel, mert ugyanazon az íven nyugvó kerületi szög a

k_{1}

körben. Minthogy egy húr két végpontjában húzott érintők egyenlő szöget zárnak be a húrral, tehát a

t_{2}

érintő az

E C

húrral ugyanakkora

δ

szöget zár be, mint a

t_{3}

érintő. A

t_{3}

érintő és

B C

húr szöge:

γ + δ

.
Az

F E C ∢

ugyanakkora, mint a

γ ∢

, mert

α

-t olyan szöggé egészíti ki, mely

β

-val együtt

180^{\circ}

-ot ad. Ebből következik, hogy a

t_{1}

és

t_{2}

érintők szöge is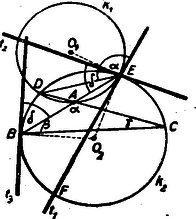

γ + δ

Ha a tetszőlegesen választott

A

pontot a

k_{1}

kör

k_{2}

-be eső ívén választjuk, akkor ugyanazokat a jelöléseket alkalmazva a

D E B ∢

ugyanakkora, mint a

γ

(ugyanazon az íven nyugvó kerületi szög), a

B E F ∢

pedig ugyanakkora, mint a

β

, mert a

\begin{matrix} D E F ∢ = 180^{\circ} - α = γ + β . \end{matrix}

Tehát a

t_{3}

érintő és

B C

húr szöge ugyanakkora, mint a

t_{1}

és

t_{2}

érintők szöge, mind a két szög:

\begin{matrix} δ + β -val egyenlő . \end{matrix}

Megoldotta: Kántor S., Rédly E., Zobor E.