| Feladat: | 274. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Béres A. , Cser Ilona , Dávid P. , Durst E. , Dömölki B. , Gergely A. , Guszti S. , Kálmán L. , Kántor S. , Kovács L. , Lipák J. , Müller Z. , Oláh J. , Osztein P. , Papp I. , Pipó Margit , Sajó J. , Szabó Magda , Szathury Éva , Tisovszky J. , Villányi O. , Zobor E. | ||
| Füzet: | 1951/november, 133 - 135. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Geometriai transzformációk, Húrnégyszögek, Síkgeometriai számítások trigonometria nélkül körökben, Szögfüggvények, síkgeometriai számítások, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1951/március: 274. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: a) Jelöljük a körön felvett pontot -vel, a belőle kiinduló húrok másik végpontjait , és -vel. 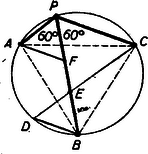 Nyilván és (ugyanazon íven álló kerületi szögek) tehát az két szögéről közvetlenül látjuk, hogy , csak ezzel bizonyítva is van, hogy a kérdéses háromszög egyenlőoldalú. b) Rajzoljunk a -ből induló középső húr végpontjában a húrral -os szöget bezáró egyenest, messe ez a kört a pontban. Kössük össze pontot -vel, és egyenesek metszéspontját jelöljük -vel. A szerkesztés szerint és szabályos, -nél fekvő szögét -osnak rajzoltuk, pedig ugyanazon a köríven áll, mint a , tehát . Továbbá , eszerint a is szabályos, mert -nél levő szöge is , tehát . Összefoglalva a két eredményt Megoldotta: Kovács L. Másrészt és , tehát és így . Megoldotta: Béres A., Gergely A., Kálmán L., Müller Z., Papp I., Szabó Magdolna, Tisovszky J., Zobor E. III. megoldás: szélső húr fölé rajzoljunk szabályos háromszöget, ennek harmadik, csúcspontja nyilván meghosszabbításába esik és egyenlő a két szélső húr összegével. 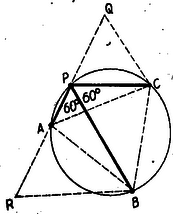 Továbbá tehát egyúttal egyenlő a középső húrral, -vel. Megoldotta: Kántor S. IV. megoldás: A középső húr fölé rajzolt szabályos háromszög segítségével és egybevágósága alapján bizonyították be a tételt. Megoldotta: Durst E., Oláh J., Szathury Éva. Másféle segédábrát használt fel: Cser Ilona, Guszti S., Lipák J., Osztein P. V. megoldás: Ptolemaius tétele szerint a húrnégyszögben az átlók szorzata egyenlő a szemközti oldalak szorzatainak összegével. Alkalmazzuk a tételt az négyszögre: Megoldotta: Dömölki B., Sajó J., Villányi O. Trigonometriai összefüggések felhasználásával oldotta meg: Dávid P., Durst E., Pipó Margit. Csak a tétel részét bizonyította be: Dievald Emília, ifj. Csonka P., Főző Éva, Rasztovich M., Tilesch F., Zatykó L. |