Kezdőlap


Feladat:	252. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1951/augusztus, 75 - 77. oldal		PDF \| MathML
Témakör(ök):	Számtani-mértani egyenlőtlenségek, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1950/október: 252. matematika feladat

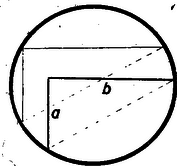
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Kössük össze a szögszárak körrel való metszéspontjait. Húzzunk ezzel a húrral párhuzamos átmérőt és a végpontjaiban a szögszárakkal párhuzamost.

Ezek a párhuzamosok kell hogy a körön messék egymást, mert azon pontok mértani helye, amelyből egy távolság derékszögben látszik, a távolság mint átmérő fölé rajzolt kör. Az így keletkezett háromszögek hasonlóak és az a nagyobb, melynek átfogója körátmérő, tehát a befogók összege is ebben nagyobb. Minden derékszöghöz a körben találunk tehát olyan kerületi szöget, melynek szárain a körbe eső szakaszok összege nagyobb. Elég tehát az átmérő fölé rajzolt derékszögű háromszögek közt keresni, hogy melyikben a legnagyobb a befogók összege. Megmutatjuk, hogy ez az egyenlőszárú háromszögre következik be. Legyen

A B C

az egyenlőszárú és

A B C_{1}

egy tetszőleges derékszögű háromszög az

A B

átmérő fölött.

Tükrözzük a

C_{1}

-en átmenő külső szögfelezőre a

B C_{1}

oldalt. Legyen a tükörkép

C_{1} B'

. Miután a külső szögfelezőre tükröztünk,

A

C_{1}

és

B'

egy egyenesre esnek. A külső szögfelező

45^{\circ}

-os szöget zár be a befogókkal. Másrészt

A C_{1} C ∢ = A B C ∢ = 45^{\circ}

, mert közös köríven nyugvó kerületi szögek. Így a külső szögfelező átmegy

C

-n is, tehát

B C

tükörképe ránézve

B' C

. Az

A B' C ▵

-ből

A C + C B = A C + C B' > A B' = A C_{1} + C_{1} B' = A C_{1} + C_{1} B

.
Ezzel bebizonyítottuk, hogy azon derékszögeken lesz a szárak körbe eső szakaszainak összege a legnagyobb, melyeknek szárai egy átmérő végpontjain mennek keresztül, csúcsa pedig ezen átmérő feletti félkör középpontja.

II. megoldás: Jelöljük a szögszárak körbe eső szakaszainak hosszát

a

-val és

b

-vel. Bármely két pozitív

a, b

számra fennáll az

\begin{matrix} \frac{a + b}{2} \leq \sqrt[]{\frac{a^{2} + b^{2}}{2}} = \frac{\sqrt[]{a^{2} + b^{2}}}{\sqrt[]{2}} \end{matrix}

(1)

egyenlőtlenség, és az egyenlőség csak akkor állhat fenn, ha

a = b

.
Mielőtt ezt bebizonyítanánk, lássuk, hogyan szolgáltatja ez a feladat megoldását. Ha

a

és

b

a kérdéses szakaszok,

a + b

és vele

\frac{a + b}{2}

értéke is akkor a legnagyobb, ha a jobboldal a lehető legnagyobb és a baloldal egyenlő vele, feltéve, hogy ez az eset bekövetkezhet. A jobboldal számlálójának geometriai értelme a szögszárak metszéspontjai közti húr hossza. Ez akkor a legnagyobb, ha e húr éppen egy átmérő. Ez esetben is a baloldal akkor és csakis akkor egyenlő vele, ha

a = b

, vagyis egy átmérő fölé rajzolt egyenlőszárú derékszögű háromszög szárai.
Megoldásunk tehát teljes lesz, ha bebizonyítjuk az (1) egyenlőtlenséget. Elég helyette a két oldal négyzete közt a megfelelő egyenlőtlenséget bizonyítani, mert mindkét oldalon pozitív szám áll és pozitív számok közül az a nagyobb, amelyiknek a négyzete nagyobb. Bizonyítsuk be tehát, hogy^{$^{*}$}

\begin{matrix} {(\frac{a + b}{2})}^{2} \leq \frac{a^{2} + b^{2}}{2} . \end{matrix}

Azt mutatjuk meg, hogy a két oldal különbsége nem lehet negatív:

\begin{matrix} \frac{a^{2} + b^{2}}{2} - {(\frac{a + b}{2})}^{2} = \frac{2 a^{2} + 2 b^{2} - a^{2} - 2 a b - b^{2}}{4} = \frac{a^{2} - 2 a b + b^{2}}{4} = {(\frac{a - b}{2})}^{2} \geq 0, \end{matrix}

és egyenlőség csak akkor áll fenn, ha

a = b

. Ebből következik, hogy a fönti egyenlőség, s így megjegyzésünk szerint, az is hogy (1) fennáll és egyenlőség ezekben is csak akkor állhat, ha

a = b

III. megoldás: Rajzoljunk tetszőleges törött vonalat, melynek minden szakasza egy adott egyenessel ugyanakkora szöget zár be.

Nyilvánvaló, hogy ennek összhossza akkor a leghosszabb, amikor vetülete az egyenesen a leghosszabb. (Természetesen ha az egyenes egy szakaszára a törött vonal több darabjának vetülete esik, akkor ezt a szakaszt megfelelően többször vesszük számba a vetületben is.)
Húzzuk meg az adott derékszög külső szögfelezőjét. Ez mindkét szögszárral ugyanakkora (

45^{\circ}

-os) szöget zár be. Vetítsük rá a derékszög szárait. Ez a vetület ugyanakkora, mint annak a húrnak a vetülete, melyet a szög szárai vágnak ki a körből. Nem lehet tehát hosszabb a vetület, mint a kör átmérője. Az átmérővel egyenlő hosszú akkor lesz, ha a derékszög átmérőn nyugszik és ez az átmérő párhuzamos a meghúzott külső szögfelezővel. Ez akkor következik be, ha az átmérő és a szögszárak egyenlőszárú derékszögű háromszöget határolnak.

Megjegyzés: Ezzel egyúttal egyszerű geometriai bizonyítást nyertünk az előző megoldásban használt egyenlőtlenségre is.

^{$^{*}$}Az egyenlőtlenség következik

236^{*}

feladatban bizonyított egyenlőtlenségből is, ha abba

c = d = 1

-et helyettesítünk.