Kezdőlap


Feladat:	249. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1951/május, 38 - 39. oldal		PDF \| MathML
Témakör(ök):	Fizikai jellegű feladatok, Mértani helyek, Csúszásmentes (tiszta) gördülés, Feladat
Hivatkozás(ok):	Feladatok: 1950/október: 249. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A nagy kör középpontját jelöljük $O$ -val, a kicsiét $Q$ -val. Induljunk ki abból a helyzetből, mikor a kis kör megfigyelt pontja $(P)$ éppen a nagy körrel érintkező pont annak egy $B$ pontjában. Ekkor $O Q$ egybeesik $O B$ -v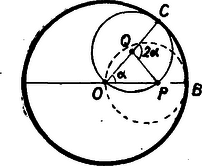el.

Gördítsük tovább a kis kört úgy, hogy

O Q

α

szöget zárjon be

O B

-vel. Az érintkezési pont legyen ebben a helyzetben

C

. Nyilván a kis körnek gördülésben részt vett

C P

íve egyenlő a nagy

C B

ívével és így a sugarak aránya miatt a

Q

-nál keletkezett szög

2 α

. De

P O C ∢

, mint kerületi szög a

P Q C ∢

fele, vagyis

α

. Másrészt

C

a két kör érintkezési pontja s így

O

Q

és

C

egy egyenesen fekszik. Így

P

O Q

-val

α

szöget bezáró egyenesen, vagyis a

B O

átmérőn van.
A meggondolás érvényes, míg

2 α \leq 180^{\circ}

, vagyis míg

C

B O

-ra merőleges átmérő végpontjáig jut. Mivel

P

B O

átmérő

B

-vel átellenes végpontjában ismét az érintkezési pontba kerül, így a körív második negyedével érintkező kis köröket tekinthetjük úgy, mintha ebből az átellenes helyzetből visszafelé görgetnénk egy kis kört. A pálya hátralevő szakaszán viszont a már tekintetbe vett mozgással szimmetrikusan mozog a kis kör. Így amit a mozgás első negyedében találtunk, az végig érvényes lesz. A

P

pont a kör egy átmérőjén mozog. Amíg a kis kör körülgördül a nagyon, addig

P

egyszer járja be oda-vissza az átmérőt.