Feladat: 235. matematika feladat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Zobor Ervin 
Füzet: 1951/május, 27 - 28. oldal  PDF  |  MathML 
Témakör(ök): Elsőfokú (és arra visszavezethető) egyenlőtlenség-rendszerek, Feladat
Hivatkozás(ok):Feladatok: 1950/október: 235. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A feltétel szerint

0<a<1(1)
és
0<b<1.(2)
A (2) feltételből következik, hogy 1-b>0. Ha az (1) egyenlőtlenséget egy pozitív számmal szorozzuk, az egyenlőtlenség helyes egyenlőtlenségbe megy át, vagyis
0<a(1-b)<1-b,
azaz felhasználva (2) baloldalát
0<a-ab<1-b,0<b<a-ab+b<1,
Ez pedig a bizonyítandó egyenlőtlenség volt.
 

Zobor Ervin (II. gimn., Nagykanizsa)
 

II. megoldás: Elég kimutatni annak az egyenlőtlenségnek fennállását, mely a bizonyítandóból úgy keletkezik, ha 1-et mindenütt levonunk:
-1<-1+a+b-ab<0;
ez pedig azt jelenti, hogy a középső kifejezés negatívja 0 és +1 közé esik:
0<1-a-b+ab<1.
(Azt is mondhattuk volna, hogy -1-el végig szorzunk, az egyenlőtlenség jeleket mindenütt ellenkezőre változtatva, azután fordított sorrendben írjuk fel az egyenlőtlenséget.)
De
1-a-b+ab=(1-a)(1-b)
és itt a feltevés szerint mindegyik tényező pozitív és 1-nél kisebb, tehát a szorzat is.
 

III. megoldás: Szemléltessük az adatokat területtel. Rajzoljunk egy egység oldalú négyzetet. Két szomszédos oldalára mérjük fel a-t és b-t és a végpontokból húzzunk párhuzamost az oldalakkal !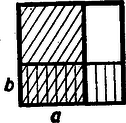
 
 

A függőlegesen vonalkázott téglalap területe b⋅1=b, a ferdén vonalkázotté a⋅1=a, a kétszeresen vonalkázott téglalap területe ab. Az a+b-ab érték az egész bevonalkázott rész területét adja. Ez a terület nem válik zérussá, ha a>0 és b>0, és nem fedi le az egységnyi területű négyzetet, ha a<1 és b<1, tehát fennáll a
0<a+b-ab<1
egyenlőtlenség.
 

Megjegyzés: A beküldött megoldásokban az a helytelen következtetés szerepelt, hogy egyenlőtlenségek különbsége is helyes egyenlőtlenség.