Kezdőlap


Feladat:	209. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1951/március, 272 - 274. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Alakzatok szimmetriái, Számtani-mértani egyenlőtlenségek, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1950/május: 209. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szimmetria középpontját egyelőre vegyük fel tetszőlegesen. Világos, hogy a felvett $P$ pontra nézve szimmetrikus sokszögek közül maximális területű az az idom lesz, amelyet az adott $A B C$ háromszög és ennek $P$ pontra tükrözöttje, $A' B' C'$ háromszög egyaránt lefed, mert minden más $P$ pontra szimmetrikus, a háromszög belsejében fekvő idom beleesik e közös részbe is.
Ezek után az a kérdés, melyik az a $P$ pont, amelyre nézve tükrözve a háromszöget, a két háromszög közös részének területe a lehető legnagyobb?
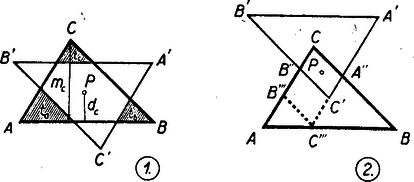
Jelöljük a szokásos módon a háromszög magasságvonalait $m_{a}$ , $m_{b}$ , $m_{c}$ -vel, $P$ pont távolságait az egyes oldalaktól $d_{a}$ , $d_{b}$ , $d_{c}$ -vel. Feltehető, hogy

\begin{matrix} d_{a} \leq \frac{m_{a}}{2}, d_{b} \leq \frac{m_{b}}{2}, d_{c} \leq \frac{m_{c}}{2} . \end{matrix}

Ellenkező esetben ugyanis az

A B C

háromszög tükörképének valamelyik csúcspontja a háromszög belsejébe esik és (l. a 2. ábrát!) az

A'' C''' B''' C

paralelogramma olyan idom, mely középpontjára nézve tükrös tulajdonságú, tehát a feladat követelményének megfelel és a területe nagyobb, mint a két háromszög közös részének területe.
Ismeretes, hogy az

m

-ek és

d

-k között fennáll a következő összefüggés^{$^{*}$}

\begin{matrix} \frac{d_{a}}{m_{a}} + \frac{d_{b}}{m_{b}} + \frac{d_{c}}{m_{c}} = 1. \end{matrix}

(1)

A közös rész területe akkor lesz a legnagyobb, ha az

A B C

háromszögből kimaradt (bevonalkázott) háromszögek területének összege minimális. Jelöljük a kimaradó háromszögek területeit

t_{a}

t_{b}

t_{c}

-vel, összegüket

y

-nal,

A B C ▵

területét

T

-vel. Valamely kis háromszög területe úgy aránylik az

A B C ▵

területéhez, mint magasságaik négyzete, tehát pl.

\begin{matrix} \frac{t_{a}}{T} = \frac{{(m_{a} - 2 d_{a})}^{2}}{m_{a}^{2}} \end{matrix}

ebből

\begin{matrix} t_{a} = {(1 - 2 \frac{d_{a}}{m_{a}})}^{2} T \end{matrix}

összegük

\begin{matrix} y = T [{(1 - 2 \frac{d_{a}}{m_{a}})}^{2} + {(1 - 2 \frac{d_{b}}{m_{b}})}^{2} + {(1 - 2 \frac{d_{c}}{m_{c}})}^{2}] . \end{matrix}

A szögletes zárójelben levő kifejezés harmadrésze három négyzet számtani közepe. Ez a négyzetes közép nagyobb vagy egyenlő a három mennyiség számtani közepének négyzeténél^{$^{*}$}, következésképpen (felhasználva (1)-et)

\begin{matrix} y \geq 3 T {[\frac{(1 - 2 \frac{d_{a}}{m_{a}}) + (1 - 2 \frac{d_{b}}{m_{b}}) + (1 - 2 \frac{d_{c}}{m_{c}})}{3}]}^{2} = \\ = 3 T {\frac{1}{3} [3 - 2 (\frac{d_{a}}{m_{a}} + \frac{d_{b}}{m_{b}} + \frac{d_{c}}{m_{c}})]}^{2} = \frac{1}{3} T . \end{matrix}

y

akkor minimális, ha az egyenlőség áll fenn, ami akkor és csakis akkor következik be, ha a kis zárójelben levő mennyiségek egyenlők, ez esetben pedig

\begin{matrix} \frac{d_{a}}{m_{a}} = \frac{d_{b}}{m_{b}} = \frac{d_{c}}{m_{c}} = \frac{1}{3} . \end{matrix}

(2)

A legutolsó egyenlőség (1)-ből következik.)
(2) szerint

P

pont az

A B C ▵

súlypontja és adott háromszögbe írható, egy pontra szimmetrikus és maximális területű az a sokszög, mely a háromszög és a háromszög súlypontjára vonatkozó tükörképének közös része. E közös rész területe

\frac{2}{3}

-a a háromszögének.

Megjegyzés: A tétel megfelelője fennáll a térben is, ha háromszög helyett tetraédert mondunk és a beírható egy pontra szimmetrikus maximális köbtartalmú poliédert keressük. Bizonyítható, bogy ez a tetraéder és a súlypontjára tükrözött tetraéder közös része. A bizonyítás megegyezik a háromszögre adott bizonyítással.

^{$^{*}$}Az egyes törteket a megfelelő oldal hosszával bővítve a nevezők értéke megegyezik, s ugyanazt a területet jelenti, mint a számlálók összege.

^{$^{*}$}Legyen ugyanis $p$ , $q$ , $r$ három tetszőleges pozitív szám, és a számtani közepük $s = \frac{p + q + r}{3}$ . Legyen $p = s + x$ , $q = s + y$ , $r = s + z$ . Ekkor

\begin{matrix} x + y + z = 0, s így \frac{p^{2} + q^{2} + r^{2}}{3} = \frac{3 s^{2} + 2 (x + y + z) s + x^{2} + y^{2} + z^{2}}{3} = \end{matrix}

\begin{matrix} = s^{2} + \frac{x^{2} + y^{2} + z^{2}}{3} \geq s^{2} = {(\frac{p + q + r}{3})}^{2} . \end{matrix}

Egyenlőség csak az

x = y = z = 0

, azaz

p = q = r

esetben állhat fenn.