| Feladat: | 203. matematika feladat | Korcsoport: 14-15 | Nehézségi fok: nehéz |
| Füzet: | 1951/március, 267 - 268. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kombinatorikai leszámolási problémák, Logikai feladatok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1950/május: 203. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Egyelőre ne törődjünk azzal a tilalommal, hogy a lépések során a figura nem haladhat át olyan mezőn, amelyen másik figura áll, ekkor (egyirányú) lépés alatt minden mezőt egyszer fog érinteni. Hasonló, de egyszerűbb esetet valósíthatunk meg, ha a feladatot úgy módosítjuk, hogy minden figura, ahelyett, hogy négy mezőt átugorna, a szomszédos mezőre lépjen. A módosított feladat megoldása világos: az egymásra lépés tilalmát is figyelembe véve a figurák ugyanabban a ciklikus sorrendben bárhogyan visszakerülhetnek az eredeti helyekre, ami négyféleképpen történhetik. 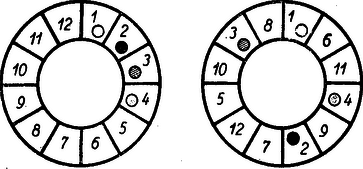 Az eredeti feladatot ezután a módosított feladatra úgy vezethetjük vissza, ha a mezők sorrendjét valamelyik, pl. a vörös figura lépéseinek megfelelően változtatjuk meg a 2. ábra szerint. Mikor valamelyik figura az első ábrán valamelyik irányban négy mezőt kihagyva az ötödikre lép, akkor ugyanez a figura a 2. ábrán egy szomszédos mezőre lép és megfordítva. Ha tehát a négy figurát ráhelyezzük a 2. ábra 1, 2, 3 és 4-es mezőire, az lesz a feladatunk, hogy ezeket bizonyos számú lépéssel más sorrendben ugyanezekre a mezőkre juttassuk vissza, úgyhogy minden figura mindig szomszédos mezőre lépjen, feltéve, hogy ott még nem áll figura. Világos, hogy ez most is négyféleképpen történhet, a figurák ciklikus sorrendjének megváltoztatása nélkül. Megjegyzés. Pontosan ugyanezzel a gondolatmenettel bizonyítható be, hogy ha a kör kerületén mező van és ezek közül -n különböző figura áll, és minden figura mezőt átugorva az -edik mezőre helyezhető (Ha ott még figura nem áll), a figurák akkor is a ciklikus sorrend megtartásával, vagyis -féleképpen juthatnak vissza az eredeti mezőkre, feltéve, hogy és relatív prímek. Csak ez utóbbi megszorítás mellett kerülhet rá a lépések folyamán minden figura bármelyik mezőre, aminek lehetőségét a bizonyításban kihasználtuk. Ha pedig és nem relatív prímek, akkor a mezők több csoportra bomlanak és a különböző csoportokhoz tartozó figurák egymás lépéseit nem befolyásolják. Így pl. ha az eredetileg kitűzött feladatban , akkor a páros mezőn álló figura sohasem kerülhet páratlanra és viszont. Ilyenkor külön-külön marad változatlan az egyes csoportokhoz tartozó figurák ciklikus sorrendje. |