Kezdőlap


Feladat:	194. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	László Z.
Füzet:	1951/március, 258 - 259. oldal		PDF \| MathML
Témakör(ök):	Alakzatok köré írt kör, Feladat
Hivatkozás(ok):	Feladatok: 1950/május: 194. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) (az 1. megoldás általánosítása). A következő old. ábráján feltüntetett jelölésekkel elegendő azt bizonyítani, hogy

\begin{matrix} A B D ∢ = A C D ∢, \end{matrix}

(1)

mert ez esetben

A B C D

négyszög húrnégyszög.

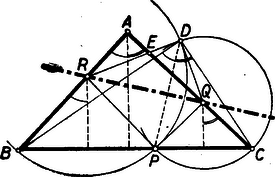A szerkesztésből következik, hogy

B R = R P

és

P Q = Q C

. Másrészt azonban a tükrözés miatt

P R = D R

és

P Q = D Q

. Ezekből az egyenlőségekből következik, bogy a

B R D

és a

C Q D

háromszögek most is egyenlőszárúak. A bizonyítandó (1) állítást helyettesíthetjük azzal, hogy e háromszögek csúcsnál fekvő szögeinek, illetve ezek mellékszögeinek egyenlőségét mutatjuk ki, tehát azt, bogy

\begin{matrix} A R D ∢ = A Q D ∢ . \end{matrix}

(2)

Tekintsük ismét az

A R E

és

E Q D

háromszögeket, melyek

E

-nél fekvő szögei csúcsszögek s így (2) állításunk igazolására harmadik szögük egyenlőségét kell kimutatnunk:

\begin{matrix} R D Q ∢ = R A Q ∢ . \end{matrix}

Ezek közül a baloldali szög

R D Q ∢ = R P Q ∢

a tükrözés folytán, míg a jobboldali benne van az

A B C ▵

-ben, eszerint

\begin{matrix} R A Q ∢ + Q C P ∢ + P B R ∢ = 180^{\circ} \end{matrix}

C P Q ▵

és

B P R ▵

tükrösségéből következik, hogy

\begin{matrix} Q C P ∢ = Q P C ∢ és D B R ∢ = B P R ∢, \end{matrix}

tehát

R A Q ∢

-et a

Q P C ∢

és

B P R ∢

-ek összege

180^{\circ}

-ra egészíti ki, ebből következik, hogy

\begin{matrix} R A Q ∢ = R P Q ∢, \end{matrix}

ami éppen bizonyítandó volt.
A második megoldás nem általánosítható, mert egyrészt azt használja ki, hogy

A B C ∢ = A C B ∢

, másrészt azt, hogy

A R Q D

szimmetrikus trapéz.

b.) (a 3. megoldás általánosítása). Éppen úgy, mint a speciális esetben, itt is a

C

P

és

D

pontokon áthaladó kör középpontja

Q

, a

B

P

és

D

pontokon áthaladóé:

R

.
Ismét alkalmazva a kerületi szögek tételét

\begin{matrix} C D P ∢ = \frac{1}{2} C Q P ∢ \end{matrix}

és

\begin{matrix} P D B ∢ = \frac{1}{2} P R B ∢ . \end{matrix}

Adjuk össze a két egyenlőséget:

\begin{matrix} C D B ∢ = \frac{1}{2} (C Q P ∢ + P R B ∢) = \frac{1}{2} [(180^{\circ} - 2 Q C P ∢) + (180^{\circ} - 2 R B P ∢)] = \\ = 180^{\circ} - Q C P ∢ - R B P ∢ = B A C ∢, \end{matrix}

és így

A

és

D

ugyanazon a

B

és

C

pontokon áthaladó köríven van.

A 4. megoldás nem általánosítható, már a szimmetrikus trapéz felhasználása miatt sem.