Kezdőlap


Feladat:	191. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1950/október, 214 - 217. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Sokszögek szerkesztése, Teljes indukció módszere, Feladat
Hivatkozás(ok):	Feladatok: 1950/március: 191. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ez a feladat hasonló az 1. számban közölt ,,Mi is a teljes indukció?'' című cikk 8. feladatához, csak ott $φ$ helyett is $α$ áll, és nem cosinusokat, hanem sinusokat összegeztünk. Hasonlóan is bizonyíthatjuk az azonosságot, mint annál a feladatnál tettük.

I. Megoldás: Bizonyíthatjuk az állítást teljes indukcióval. Jelöljük a baloldali összeget

C_{n}

-nel.
Ha

n = 1

C_{1} = cos α

, és a jobboldalon is

cos α

áll, vagyis

n = 1

esetben az állítás igaz.
Tegyük fel most valamely

k

-ra már igazoltuk az állítást:

\begin{matrix} C_{k} = \frac{cos (\frac{(k - 1) φ}{2} + α) sin \frac{k}{2} φ}{sin \frac{φ}{2}}; \end{matrix}

nézzük meg, igaz marad-e

n = (k + 1)

esetre is.

\begin{matrix} C_{k + 1} = C_{k} + cos (k φ + α) = \frac{cos (\frac{(k - 1) φ}{2} + α) sin \frac{k}{2} φ}{sin \frac{φ}{2}} + cos (k φ + α) = \\ = \frac{cos (\frac{(k - 1) φ}{2} + α) sin \frac{k}{2} φ + cos (k φ + α) sin \frac{φ}{2}}{sin \frac{φ}{2}} = \\ = \frac{\frac{1}{2} [sin (\frac{(2 k - 1) φ}{2} + α) - sin (α - \frac{φ}{2})]}{sin \frac{φ}{2}} + \frac{\frac{1}{2} [sin (\frac{(2 k + 1) φ}{2} + α) - sin (\frac{(2 k - 1) φ}{2} + α)]}{sin \frac{φ}{2}} = \\ = \frac{\frac{1}{2} [sin (\frac{(2 k + 1) φ}{2} + α) - sin (α - \frac{φ}{2})]}{sin \frac{φ}{2}} = \frac{cos (\frac{k φ}{2} + α) sin \frac{k + 1}{2} φ}{sin \frac{φ}{2}} \end{matrix}

vagyis az állítás igaz az

n = (k + 1)

esetre is. Így az állítás minden

n

-re igaz.

II. Megoldás: Vizsgáljuk mindkét oldalnak a

sin \frac{φ}{2}

-szeresét, tehát azt bizonyítsuk be, hogy

sin \frac{φ}{2} C_{n} = cos (\frac{(n - 1) φ}{2} + α) sin \frac{n}{2} φ

.
A baloldalon csupa ilyen tagot kapunk:

\begin{matrix} sin \frac{φ}{2} cos (k φ + α) = \frac{1}{2} [sin (\frac{(2 k + 1)}{2} φ + α) - sin (\frac{(2 k - 1) φ}{2} + α)] \end{matrix}

és így,

\begin{matrix} sin \frac{φ}{2} C_{n} = \frac{1}{2} [sin (\frac{φ}{2} + α) - sin (α - \frac{φ}{2}) + sin (\frac{3 φ}{2} + α) - \\ - sin (\frac{φ}{2} + α) + ... + sin (\frac{(2 n - 3) φ}{2} + α) - sin (\frac{(2 n - 5) φ}{2} + α) + \\ + sin (\frac{(2 n - 1) φ}{2} + α) - sin (\frac{(2 n - 3) φ}{2} + α)] = \\ = \frac{1}{2} [sin (\frac{(2 n - 1) φ}{2} + α) - sin (α - \frac{φ}{2})] = cos (\frac{(n - 1) φ}{2} + α) sin \frac{n}{2} φ . \end{matrix}

Ezzel a bizonyítandó összefüggést nyertük.

III. Megoldás: Az összeg könnyen szemléltethető geometriailag is. Húzzunk egy egyenest és rajzoljunk ennek egy

A_{0}

pontjából az egyenessel

α

szöget bezáró egységnyi hosszúságú

A_{0} A_{1}

szakaszt. E szakasz vetülete az egyenesen

cos α

, és

A_{1}

távolsága az egyenestől

sin α

. Most az

A_{1}

pontból rajzoljunk az

A_{0} A_{1}

egyenessel

φ

szöget bezáró egységnyi hosszúságú szakaszt. Ennek az eredeti egyenes irányával bezárt szöge

φ + α

s így az

A_{0} A_{1} A_{2}

törtvonal vetülete az egyenesre

cos α + cos (φ + α)

A_{2}

távolsága az egyenestől pedig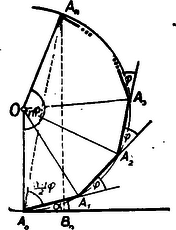

sin α + sin (φ + α)

Ezt most

n

-szer ismételve kapunk egy

A_{0} A_{1} A_{2} ... A_{n}

törtvonalat, mely egységnyi hosszúságú szakaszokból van összetéve, és két szomszédos szakasz közti szög

π - φ

. Legyen

A_{n}

vetülete az egyenesen

B_{n}

akkor

\begin{matrix} A_{0} B_{0} = cos α + cos (φ + α) + ... + cos ((n - 1) φ + α) = C_{n}, \\ A_{n} B_{n} = sin α + sin (φ + α) + ... + sin ((n - 1) φ + α) = S_{n} . \end{matrix}

A keletkező törtvonal csúcsain át kör fektethető. Húzzuk meg ugyanis a szomszédos szakaszok közti szög felezőit is. Húzzunk a kezdő és végpontban is az első, illetve az utolsó szakasszal

\frac{π - φ}{2}

nagyságú szöget bezáró egyeneseket. Ekkor minden szakasz fölé egybevágó egyenlőszárú háromszögeket szerkesztettünk. A szomszédosaknak egy-egy szára közös s így az összesek csúcsa egy közös

O

pontba kell, hogy essék.
Ezt tudva már nem nehéz a meghatározandó

C_{n}

és

S_{n}

összeget ábrázoló

A_{0} B_{n}

és

A_{n} B_{n}

távolságokat kiszámítani. Az

A_{0} B_{n} A_{n} ▵

-ből

A_{0} B_{n} = A_{0} A_{n} cos B_{n} A_{0} A_{n} ∢

és

A_{n} B_{n} = A_{0} A_{n} sin B_{n} A_{0} A_{n} ∢

A_{0} O A_{n} ▵

-ből

A_{0} A_{n} = 2 A_{0} O sin \frac{A_{0} O A_{n} ∢}{2}

Így a

B_{n} A_{0} A_{n}

szöget, a kör

A_{0} O

sugarát és az

A_{0} O A_{n}

középponti szöget kell meghatároznunk. Ezek közül az utolsó

n

egybevágó egyenlőszárú háromszög szögeiből tevődik össze. Mivel az alapnál fekvő szögek mindegyike

\frac{π - φ}{2}

, így vele szemben

φ

nagyságú szög van, amiből

A_{0} O A_{n} ∢ = n φ

.
Az egyenlőszárú háromszögek alapja egységnyi hosszúságú, így azt kapjuk, hogy

\begin{matrix} sin \frac{φ}{2} = \frac{\frac{1}{2}}{A_{0} O}, tehát A_{0} O = \frac{1}{2 sin \frac{φ}{2}} . \end{matrix}

Végül szerkesztés szerint

B_{n} A_{0} A_{1} ∢ = α

A_{1} A_{0} A_{n} ∢

pedig mint kerületi szög az

A_{1} O A_{n} ∢

fele. Az előbbi meggondolás szerint utóbbi szög

(n - 1) φ

tehát

B_{n} A_{0} A_{n} ∢ = \frac{n - 1}{2} φ + α

.
Így

\begin{matrix} cos α + cos (φ + α) + cos (2 φ + α) + ... + cos [(n - 1) φ + α] = A_{0} B_{n} = \frac{sin \frac{n}{2} φ cos [\frac{n - 1}{2} φ + α]}{sin \frac{φ}{2}} \end{matrix}

és ezt kellett bizonyítanunk; továbbá

\begin{matrix} sin α + sin (φ + α) + sin (2 φ + α) + ... + sin [(n - 1) φ + α] = A_{n} B_{n} = \frac{sin \frac{n}{2} φ sin [\frac{n - 1}{2} φ + α]}{sin \frac{φ}{2}} . \end{matrix}

Utóbbiban

α

helyébe

φ

-t írva a már ismert eredményt kapjuk vissza.