Kezdőlap


Feladat:	171. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1950/március, 83 - 86. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Derékszögű háromszögek geometriája, Szinusztétel alkalmazása, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1948/szeptember: 171. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Számítással nem sok nehézséget ad a feladat megoldása. Általában megmutatjuk, hogy az összes olyan háromszögek közül, melyeknek egyenlő a kerülete és ezen kívül egyenlő a $γ$ szögük, abban lesz az ezzel szemközti $c$ oldal a legkisebb, melyben $α = β$ . Kifejezzük a kerületet a $c$ oldal segítségével. A sinus-tétel szerint

\begin{matrix} k = a + b + c = \frac{c sin α}{sin γ} + \frac{c sin β}{sin γ} + c = \frac{c}{sin γ} (sin α + sin β + sin γ) = \\ = \frac{c}{2 sin \frac{γ}{2} cos \frac{γ}{2}} (2 sin \frac{α + γ}{2} cos \frac{α - β}{2} + 2 sin \frac{γ}{2} cos \frac{γ}{2}) = \frac{c}{2 sin \frac{γ}{2}} (cos \frac{α - β}{2} + sin \frac{γ}{2}) . \end{matrix}

Innen

\begin{matrix} c = \frac{k sin \frac{γ}{2}}{cos \frac{α - β}{2} + sin \frac{γ}{2}} \end{matrix}

A jobb oldalon csak a nevező első tagja változhat,

c

akkor a legkisebb, ha ez a tag legnagyobb, tehát ha

α = β

II. megoldás: Az eredmény olyan egyszerű, hogy érdemes megpróbálni, kevesebb geometriai ismeret felhasználásával, számolás nélkül is bebizonyítani. Eredeti formájában azért nehéz hozzáfogni a kérdéshez, mert az ismert távolság, a kerület három oldalból tevődik össze. Át lehet azonban alakítani a feladatot úgy, hogy egy oldal legyen változatlan.
Az előbbi megoldásban kimondott általánosabb alakjában bizonyítjuk ismét a tételt és ugyanazokat a jelöléseket is használjuk. Vegyünk különböző alakú olyan háromszögeket, melyeknek kerülete és

γ

szöge egyenlő. Nagyítsuk vagy kicsinyítsük őket úgy, hogy mindegyiknek egyenlő legyen a

c

oldala. Minél kisebb volt eredetileg a

c

oldal, annál nagyobb lesz az új háromszög kerülete. A háromszög alakja nem változik. Így most olyan háromszögeket kaptunk, melyekben egyenlő a

γ

szög és a vele szemben fekvő

c

oldal. Ezek közül legnagyobb lesz a kerülete annak, amelyiknek eredetileg legkisebb volt a

c

oldala. Most tehát az előbbi állítás helyett azt kell megmutatnunk, hogy azon háromszögek közül, melyeknek egyenlő egy szögük és a vele szemben levő oldaluk, az egyenlőszárúnak legnagyobb a kerülete.
Ha ezeket a háromszögeket közös

c

oldal fölé rajzoljuk le, akkor a

C

csúcsok egy köríven feküsznek. Legyen

A B C

egy tetszőleges e háromszögek közül,

A B C_{0}

, pedig az egyenlőszárú.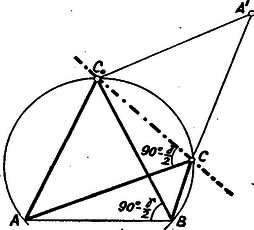

Mivel

A B

oldaluk közös, azt kell megmutatnunk, hogy

A C_{0} + B C_{0} > A C + B C

. Legyen

C

mondjuk a

B C_{0}

félíven. Mérjük

A C

-t

B C

-nek

C

-n túli meghosszabbítására, vagy ami ezzel egyet jelent, tükrözzük

A C

-t az

A B C_{Δ}

C

-ben húzott külső szögfelezőjére. A tükörképe legyen

A'

.
Ez a szögfelező az

A C

oldallal

\frac{180^{\circ} - γ}{2}

nagyságú szöget zár be, ugyanakkorát, mint amekkorák az egyenlőszárú háromszög alapján fekvő szögek. Ekkor azonban a szögfelező és a

B C_{0}

szár a körön metszik egymást, vagyis a

C

-ben húzott szögfelező átmegy a

C_{0}

-on is. Így

C_{0} A'

A C_{0}

tükörképe a

C C_{0}

egyenesre. Ezek szerint

\begin{matrix} A C_{0} + C_{0} B = A' C_{0} + C_{0} B > A' B = A' C + C B = A C + C B . \end{matrix}

Ezzel bebizonyítottuk állításunkat.

III. megoldás: Az előző megoldás utat mutat arra is, hogy próbálhatjuk meg átfogalmazás nélkül is tisztán geometriai úton bizonyítani be állításunkat. Mérjük fel az adott

P Q

kerületet és szerkesszük meg ebből kiindulva a különböző alakú, de egyenlő kerületű és egyenlő nagy

γ

szöggel rendelkező háromszögeket.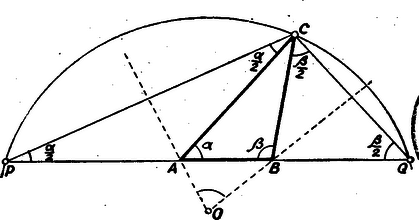

α

-t a lehetséges határok közt tetszőlegesen választjuk és megszerkesztjük a hozzá tartozó

β = 180^{\circ} - (α + γ)

szöget, ezekből a háromszög az ismert szellemes módon szerkeszthető, amit az ábra is szemléltet. A

C

pontot a

P

és

Q

-ban

α / 2

és

β / 2

szög alatt hajló egyenesek metszéspontja adja,

A

és

B

pedig egy

P C

illetve

Q C

alapú egyenlőszárú háromszög csúcsa.

\begin{matrix} P C Q ∢ = 180^{\circ} - \frac{α + β}{2} = 90^{\circ} + \frac{γ}{2}, \end{matrix}

tehát független, a másik két szög nagyságától. Így az összes háromszög

C

csúcsa egy

P

-n és

Q

-n átmenő köríven fekszik.
Az

A

és

B

csúcsot úgy is kijelölhetjük, mint a

P C

illetve

Q C

szakaszok felező merőlegesének a

P Q

egyenessel való metszéspontját. Ezeknek a merőlegeseknek a metszéspontja éppen a

P C Q Δ

köré irt kör középpontja, tehát az előbb mondottak szerint ugyanaz a pont, akármelyik háromszög megszerkesztéséről van is szó a számba jövők közül. A két merőleges szöge mint a

P C Q

száraira merőleges szárú szög

90^{\circ} - \frac{γ}{2}

nagyságú. Így arra az egyszerű eredményre jutottunk, hogy a háromszögek

c

oldalát egy

O

középpontú,

90^{\circ} - \frac{γ}{2}

nagyságú szög vágja ki a

P Q

szakaszból.
A legkisebb

c

oldallal bíró háromszög megkereséséhez tehát csak azt kell tudnunk, hogy milyen helyzetben vág ki egy adott nyílású, adott pont körül forgó szög, adott egyenesből a legkisebb szakaszt. Megmutatjuk, hogy akkor, ha a szög helyzete az egyeneshez képest szimmetrikus, vagyis ha két szára egyenlő szöget zár be az adott egyenessel, csak ellenkező irányban. Legyen

A_{0} O B_{0}

a szimmetrikus helyzetű szög,

A O B

pedig egy tetszőleges helyzetű, a pontok sorrendje a

P Q

szakaszon legyen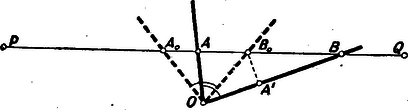

P A_{0} A B_{0} B Q

Állításunk igazolásához azt kell megmutatnunk, hogy

B_{0} B > A_{0} A

.
Másoljuk rá az

O A_{0} A Δ

-et az

O B_{0}

oldalra. Ekkor

O A

megfelelője

O B

-re fog esni. Jelöljük

A

megfelelőjét

A'

-vel. Mivel

\begin{matrix} B_{0} A' B ∢ = A' O B_{0} ∢ + O B_{0} A' ∢ > O B_{0} A' ∢ = O B_{0} A_{0} ∢ = \\ = B_{0} O B ∢ + O B B_{0} ∢ > O B B_{0} ∢ . \end{matrix}

így

\begin{matrix} B_{0} B < B_{0} A' = A_{0} A . \end{matrix}