| Feladat: | 169. matematika feladat | Korcsoport: 18- | Nehézségi fok: nehéz |
| Füzet: | 1950/február, 43 - 45. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Beírt alakzatok, Négyszögek szerkesztése, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1948/május: 169. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Először is feltehetjük, hogy a téglalap három csúcsa a háromszög oldalain fekszik. Ha ugyanis nem ez volna a helyzet, akkor eltolhatnánk a háromszög oldalait párhuzamosan addig, míg el nem érik a téglalapot, 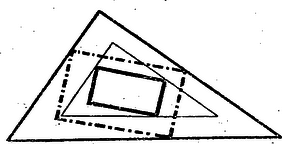 Így egy kisebb háromszöget kapunk az eredeti belsejében, melynek kerületére esik a téglalap három csúcsa, és mely hasonló az eredetihez. Nagyítsuk ezt ki akkorára, mint az eredeti, akkor kapunk annak belsejében egy téglalapot, mely nagyobb, mint az eredeti és melynek három csúcsa a háromszög oldalán fekszik. Lehet, hogy ennek a téglalapnak a negyedik csúcsa is a háromszög kerületére esik, ha az eredetinek egy oldala párhuzamos volt a háromszög egyik oldalával. Nézzük meg, hogy az ilyenek közül melyiknek legnagyobb a területe. Összehasonlíthatjuk a téglalap területét a háromszögével úgy hogy a háromszög kimaradó részeit visszahajtjuk a téglalapra. Feküdjék pl. a téglalap egyik oldala az oldalán. 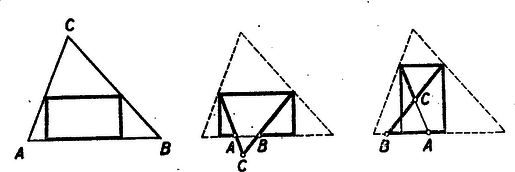 Ekkor a téglalapon kívül eső háromszögek visszahajtásánál az és csúcsok újra az egyenesre esnek, az és oldalak visszahajtott részei pedig egy egyenesbe essenek, sem hézagot nem hagynak, sem kétszeresen nem fednek Így vagy az és csúcsok újra az egyenesre esnek, az és hajtáskor, vagy kell, hogy a csúcsú háromszög visszahajtáskor a téglalapon túlnyúljon a visszahajtott és csúcsok közt. Mivel a téglalap mindenképpen teljesen le van fedve a háromszög kimaradó részével, így területe nem lehet nagyobb, mint a háromszög területének fele. Egyenlő is csak úgy lehet, ha sem kétszeres fedés, sem túlnyúló részek nem keletkeznek a behajtásnál, ez pedig csak akkor következik be a fentiek szerint, ha a visszahajtott csúcsok egybeesnek. Ez a helyzet akkor, ha a téglalapnak az egy háromszögoldalon fekvő két csúcsával szemben lévő csúcsok a másik két oldal felezőpontjai. Nézzük végül azt az esetet, ha a téglalapnak csak három csúcsa esik a háromszög kerületére. Ez esetben is beláthatnánk, hogy a háromszög kimaradó részeit a téglalapra visszahajtva, azt teljesen lefedhetjük, s e mellett mindig keletkezik dupla fedés. Körülményes volna azonban különösen az állítás első felének az igazolása. E helyett megpróbáljuk ezt az esetet is az előbbi speciális esetre visszavezetni és így megtakarítani azt, hogy meg kelljen ismételni az előbbi okoskodást. Ha a téglalap három csúcsa fekszik a háromszög kerületén, akkor is fekhet egy oldalon két csúcs, ha a háromszög tompaszögű. Az ilyen helyzetű téglalapok közül a legnagyobbnak egyik csúcsa a háromszög tompaszögű csúcsába kell hogy essék. 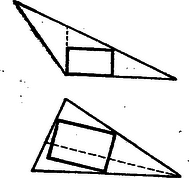 Ha a háromszög különböző oldalaira esik a három csúcs, akkor a téglalap egyik oldala sem párhuzamos a háromszög semelyik oldalával, továbbá van két szomszédos csúcs, mely a háromszög kerületén fekszik. Utóbbi esetben húzzunk merőlegest az ezek közt levő oldalra a háromszög azon csúcsából, melyben az e két csúcsot tartó oldal találkozik; az előbbi esetben hosszabbítsuk meg a téglalapnak azt az oldalát, mely háromszög-csúcsba fut, de nem fekszik a háromszög kerületén. Mindkét esetben két háromszögre vágtuk az eredetit. Mindkettőben van egy-egy téglalap (a tompaszögű háromszögnél az egyik egy egyenesszakaszra zsugorodott össze), melynek egyik oldala a háromszög egy oldalára esik és valamelyiknek csak három csúcsa esik az őt tartalmazó részháromszög kerületére. Ebbe az utóbbiba tehát biztos kisebb területű téglalap esik, mint a részháromszög területének a fele, a másik részháromszögbe eső téglalap-rész pedig nem lehet nagyobb annak a részháromszögnek a félterületénél. Így az egész téglalap területe kisebb az egész háromszög területének a felénél. Lehet tehát nála nagyobb téglalapot írni a háromszögbe. Egy háromszögbe írható legnagyobb területű téglalap tehát félakkora, mint a háromszög és úgy helyezkedik el, hogy egy oldala a háromszög egyik oldalára esik, másik két csúcsa pedig a másik két oldal felezőpontjába. Hegyesszögű háromszögnél mind a három oldalra írhatunk egy-egy ilyet, tehát összesen három különbözőt, tompaszögű háromszögnél azonban ilyen téglalap csak a leghosszabb oldalra írható, tehát csak egy van. Derékszögű háromszögnél a három téglalap közül a két befogóra rajzolt téglalap egybeesik s így csak két különböző téglalapot kapunk. |