|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az I. Évfolyam 5‐6. számában (1948. május) volt kitűzve a következő feladat.
168. Húzzunk négy egyenest, melyek metszik egymást, de nem megy át három egy ponton. Mutassuk meg, hogy véve közülük 3‐3-at az ezek által határolt háromszögek magassági pontjai egy egyenesen feküsznek.
1. Hogyan oldható meg a feladat analitikus
geometria segítségévél?
Ilyen feladatnál igen jó szolgálatot tesz az analitikus geometria, mert minden gondolkodás nélkül felírhatjuk a négy egyenes egyenletét, majd az általuk meghatározott négy háromszögnek kiszámítjuk két‐két magasságvonalát; így kiszámíthatjuk a magasságpontok koordinátáit, és megnézhetjük, hogy valamelyik két pont által meghatározott egyenesen rajta fekszik-e a másik két pont is.
Ennek a megoldásnak semmi elvi nehézsége nincs, csak éppen tényleg végig kellene számolni és ez nagyon fáradságos és unalmas volna. Igaz, hogy a sok számolás bizonyos fokig természetes, mert az analitikus geometriának épp az a célja, hogy a geometriai módszerek helyébe, amelyek igen szemléletesek, de nehezen áttekinthetőek, algebrai és függvénytani módszereket vehessünk igénybe a problémák megoldásához. Ezek a módszerek már sokkal egyszerűbb szerkezetűek és alapos gyakorlatunk is van kezelésükben.
Mégsem nyugszunk könnyen bele, hogy ilyen sokat kelljen számolni. Először megnézzük geometriai oldalról a feladatot, még mielőtt átírnánk a számok nyelvére, hogy nem lehetne-e egyszerűsíteni. Négy pontról kell megmutatni, hogy egy egyenesen feküsznek. Kezdjük először valamelyik hárommal. Ha ez sikerül, találomra választott három pontra, más szóval, ha meg tudjuk mutatni, hogy bármely három pont a négy közül egy egyenesen fekszik, akkor már könnyű befejezni a bizonyítást. Ekkor ugyanis a harmadik pont is rajta van az első kettőn átmenő egyenesen, meg erre az egyenesre esik a negyedik pont is, tehát a négy pont egy egyenesen fekszik.
Elég tehát azt megmutatni, hogy négy pont közül tetszőlegesen választott három egy egyenesen fekszik. Ahhoz, hogy ezt a kérdést az analitikus geometria nyelvére fordítsuk, koordináta-tengelyeket kell választanunk. Ezeket bárhol választhatjuk, attól nem függ a tétel helyessége. Egy ilyen szabadsággal igyekszünk helyesen élni és nem találomra választjuk a tengelyeket, hanem úgy, hogy a keletkező kifejezések lehetőleg egyszerűek legyenek.
Esetünkben három háromszöget választunk ki a négy egyenes közt keletkező négyből és ezek magassági pontjairól akarjuk megmutatni, hogy egy egyenesen feküsznek. Ekkor van egy egyenes a négy közül, mely mindhárom háromszögnek oldala. Ezt lesz jó -tengelynek választani, mert mindhárom háromszögnek egy magassága erre merőleges. A szemközti csúcs abszcisszája tehát mindjárt a magasságpont abszcisszája is lesz a tengely ilyen választásánál. Még egy-egy magasság egyenletét kell felírni és abba ezt az abszcisszát behelyettesíteni, és már megvan a magasságpont ordinátája is.
Az -tengelyt is választhatnánk speciálisan, pl. két egyenes metszéspontján át. Ez azonban már nem biztos, hogy hasznos volna. -tengelynek egy, a bizonyítandó állítás szempontjából különleges egyenest választottunk. A másik három egyenes azonban teljesen egyenlő szerepet játszik és ez a szimmetria előnyt jelenthet a számolásban is. Az -tengely speciális választása azonban arra vezetne, hogy ez a szimmetria a számításban nem mutatkoznék.
Ezen az úton már nagyobb nehézség nélkül megoldhatja mindenki a feladatot, különösen ha az említett szimmetriára is ügyel számolásaiban. Kár is volna itt a számolás részleteivel töltenünk a helyet.
Az analitikus geometria a számolás segítségével könnyűvé tesz sok bizonyítást, de egyben unalmassá. Nemcsak azért unalmas egy ilyen megoldás, mert a számozás unalmas, hanem azért is, mert végül is csak annyit mond, hogy a számolás ,,kijött'' az állítás helyes, vagy ,,nem jött ki'', az állítás helytelen, de sohse mutat rá arra, hogy milyen geometriai tényekkel függ össze, mi az oka annak, hogy helyes, vagy helytelen. Épp ezért lehetőleg nem érjük be a számolós megoldással, hanem keresünk elemi geometriai megoldást is.
2. A feladat planimetriai megoldása, Simson-egyenesek.
A feladat kitűzője a 137. feladatra is emlékeztet. Ott azt kellett bizonyítani, hogy a fent említett négy egyenes által meghatározott háromszögek köré írt négy kör egy pontban metszi egymást. Ez szögek közti összefüggésekből egész könnyen adódik.
Várható, hogy négy olyan kör, melynek egy közös pontja van és négy olyan pont, melyek egy egyenesen feküsznek, kapcsolatban vannak egymással.
Először nézzük tehát meg, hogy egy háromszög köré írt kör pontjai és a magasságpont közt nem találunk-e valami felhasználható kapcsolatot. A magasságpontot a csúcsból az oldalakra bocsátott merőlegesek adják. A körülírt kör egy tetszőleges pontjából is bocsássunk merőlegeseket a háromszög oldalaira. Ha több pontból meghúzzuk ezeket a merőlegeseket, fel fog tűnni, hogy talppontjaik mindig egy egyenesbe esnek. Valóban bebizonyítjuk, hogy ennek mindig így is kell lennie. Ezt az egyenest a háromszög ponthoz tartozó Simson-egyenesének nevezik.
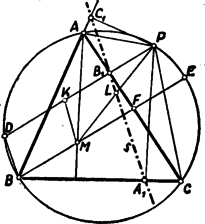
Legyen az adott háromszög a háromszög köré írt kör kerületének egy pontja. -ből a , , oldalakra bocsátott merőlegesek talppontjait jelöljük rendre , , -gyel.
1. ábra
Azt kell bebizonyítanunk, hogy , és egy egyenesen vannak. Ehhez elegendő pl. azt bebizonyítanunk, hogy az és csúcsszögek, tehát mivel a két szög egyik szára, az oldal közös, azt kell még belátni, hogy a két szög egyenlő. Azonnal észrevehetjük, hogy az és négyszögek húrnégyszögek, azaz csúcspontjaik egy kör kerületén vannak, mert az négyszögben , -ben, pedig . Most már a kívánt összefüggést megpróbálhatjuk bizonyítani kerületi szögek segítségével.
Az -en átmenő körben a -n átmenőben pedig
A jobb oldalon álló két szögben tér el a és az egymástól. Az előbbi kettő akkor egyenlő, ha az utóbbi kettő is egyenlő, ez pedig fennáll, mert ABCP húrnégyszög (a pontok a háromszög köré írt körön feküsznek). De húrnégyszög is, mert . Így és , amiből Ebből
, s így (1) és (2) egyenlőségből . , és tehát egy egyenesen feküszenek.
Megjegyezzük, hogy a bizonyítás teljes terjedelmében érvényben marad, ha , -et merőlegesség helyett úgy húzzuk, hogy az , , illetve körül ugyanabban az irányban forgatva őket egyenlő szögekkel lehessen a háromszög megfelelő oldalaira fordítani, mert csak ezeknek a forgásszögeknek az egyenlőségét használtuk fel. , és tehát ilyen esetben is egy egyenesen fekszik.
*
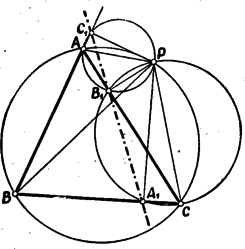
Érdekes eredményre jutottunk, csak az a hibája, hogy nincs összefüggésben a magassági ponttal. Ilyen összefüggés keresését célozta az, hogy -ből merőlegeseket állítottunk az oldalakra, mert a magasságok is a kör egy pontjából (egy csúcsból) az oldalakra bocsátott merőlegesek. Húzzuk meg a merőlegest és a csúcsból a magasságot. Ezek párhuzamos egyenesek s így a kört egy szimmetrikus trapéz csúcsaiban metszik. Legyen második metszéspontja a körrel , a -ből húzott magasságé , az oldallal való metszéspont , a magassági pont (2. ábra).
2. ábra
Tudjuk azt is, hogy és egymás tükörképe az oldalra nézve. (99. feladat I. évf. 59. 1.) Így ha -ből párhuzamost húzunk -vel, ismét szimmetrikus trapézt kapunk, de ennek szimmetriatengelyét is ismerjük: az oldal, mert folytán ez az szakasz felező merőlegese. Jelöljük e trapéz negyedik csúcsát -val, akkor a szakasz középpontja.
Ezeknek a trapézoknak azonban az Simson-egyenessel is van kapcsolatuk. Ismét az egyenlő szögeket vizsgálva , mint egyenlő ivben nyugvó kerületi szögek. Másrészt a húrnégyszögből viszont , tehát és váltószögek, így ‐ tehát is ‐ párhuzamos -sel.
Térjünk vissza és kapcsolatára. Azt tudjuk, hogy felezőpontja , ezen megy át és párhuzamos -mel. Ekkor a középvonala így felezi -et is. Ezzel bebizonyítottuk, hogy a ponthoz tartozó Simson-egyenes felezi a -ből a magassági ponthoz vezető szakaszt.
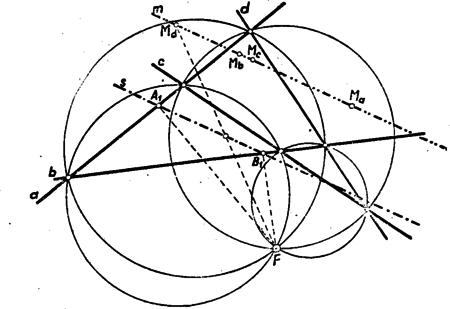
Most már olyan összefüggést ismertünk meg, amilyent reméltünk. Próbáljuk hasznosítani eredeti feladatunk megoldására. Legyen a négy egyenes , , és . Ezek közül bármelyik három meghatároz egy háromszöget. Válasszunk először két háromszöget és nézzük a köréjük irt köröket. Mivel a két háromszögnek két közös oldala van, ezek metszéspontján átmegy mind a két kör is. Tekintve azonban, hogy két kör, ha metszi egymást, akkor két pontban metszi, van még egy metszéspont, ez legyen .
3. ábra
Bármelyik háromszögre nézve az -hez tartozó Simson-egyenes átmegy a két háromszög közös oldalaira bocsátott merőlegesek talppontjain. A háromszögeknek két közös oldala lévén ez azt jelenti, hogy a két Simson-egyenes egybeesik. Ezt a négy egyenes közt fekvő bármely két háromszögre elmondhatjuk. Mivel -en mindegyik kör átmegy, következik, hogy az pontnak bármely háromszögre vonatkozó Simson-egyenese ugyanaz az egyenes.
Legyenek most az , , illetve háromszögek magasságpontjai , illetve , akkor felezi a , , , távolságokat, tehát mind a négy pont ugyanolyan messze van -től, mint , csak ellenkező oldalon. Így egy -sel párhuzamos egyenesen feküsznek.
*
A 137. feladatnál már megemlítettük, hogy a négy egyeneshez olyan parabola rajzolható, melynek a négy egyenes érintője és amelynek a fókusza. Most azt is hozzátehetjük, hogy a parabolának az irányvonala az egyenes és csúcsponti érintője az egyenes és ezt most már be is bizonyíthatjuk könnyen. Az alábbiakban ki is tűzzük feladatul.
1. Fogalmazzuk meg és bizonyítsuk be a Simson-egyenesekről szóló tétel megfordítását.
2. Hogy bizonyíthatjuk be a 137. feladatban kitűzött tételt a Simson-egyenesekről tanultak segítségével?
3. Bizonyítsuk be, hogy egy parabolának egy tetszőleges érintőjére a fókuszból merőlegest húzva a talppontja a parabola csúcsában húzott érintőre esik.
4. A cikk jelöléseit használva bizonyítsuk be, hogy azon parabolát, melynek a fókusza és a csúcsponti érintője, az , , és egyenes érinti.
Lásd, I. évf. 126. I. |
 PDF |
PDF |  MathML
MathML