Kezdőlap


Feladat:	153. matematika feladat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Baumann F. , Bernáth K. , Czibere T. és Nagy F. , Czipszer J. , Fried E. , Gacsályi Sándor , Gehér L. , Gilyén N. , Károlyházy Frigyes , Korányi Á. , Kővári T. , Markó J. , Párkány M. , Réthy Eszter , Róna P. , Salamon Á. , Szűcs L. , Tamás H. , Tarnóczi T. , Vermes R. , Vígh Magda , Vörös M.
Füzet:	1948/szeptember, 168 - 169. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1948/február: 153. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mozdítsuk el $P$ -t pl. az $A B$ oldalra merőleges irányban egy $Q$ pontba. Legyenek ennek vetületei az oldalakra $Q_{1}$ , $Q_{2}$ , $Q_{3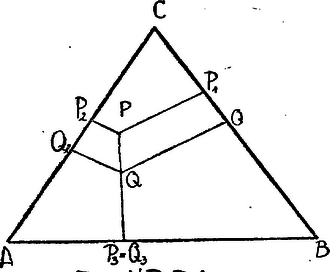}$ (51. ábra).

51. ábra

Q_{3} = P_{3}

, tehát

A P_{3}

változatlan marad.

P_{1} Q_{1}

és

P_{2} Q_{2}

közül egyik növeli, a másik csökkenti az összeget. De ez a két szakasz egyenlő, mert a

P Q

szakasz vetületei a

B C

és

A C

oldalakra, a

P Q

egyenes iránya pedig mindkét oldallal

30^{\circ}

-os szöget zár be.
Egy ilyen eltolásnál tehát nem változik a vizsgált távolságösszeg. Egy pontból a másikba azonban mindig el tudunk jutni, csak a háromszög oldalaira merőleges irányokba haladva, így bármely pontban ugyanakkora a vetületösszeg. A pontot az egyik csúcsba víve látjuk, bogy értéke mindig a fél kerület.

Károlyházy Frigyes (Bp., piar. gimn. VIII. o.)

II. megoldás. Mozdítsuk el pl. az

A B

oldallal párhuzamosan a

P

pontot egy

Q

helyzetbe.

Q

vetületei az oldalakra

Q_{1}

Q_{2}

Q_{3}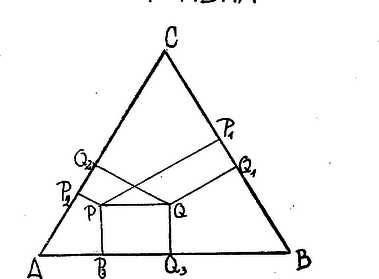

. (52. ábra).

52. ábra

P_{1} Q_{1}

és

P_{2} Q_{2}

mindkettő növeli, vagy mindkettő csökkenti az összeget,

P_{3} Q_{3}

azonban ép ellenkező értelemben változtatja.

P_{3} Q_{3} = P Q

, továbbá

P_{1} Q_{1} = P_{2} Q_{2}

, mert

P Q

iránya az

A B

és

B C

oldalakéval egyformán

60^{\circ}

-os szöget zár be. Legyen

Q

vetülete

P P_{1}

-en (vagy a meghosszabbításán)

R

, ekkor a

P Q R

derékszögű háromszögben

Q R

-rel szemben

30^{\circ}

-os szög fekszik s így

Q R (= Q_{1} P_{1}) =^{1} /_{2} P Q

. Így

P_{1} Q_{1} + P_{2} Q_{2} = P Q

, tehát az összeget ugyanannyival növeltük, mint csökkentettük.
Mivel minden pontból bármelyikbe el lehet jutni az oldalakkal párhuzamos utakon is, tehát tételünk igaznak bizonyult.

III. megoldás. Legyen a

P_{1}

ből

A B

-re emelt merőleges talppontja

Q_{3}

P_{2}

-ből

B C

-re emelt merőlegesé

Q_{1}

P_{3}

-ból

A C

-re emelt merőlegesé

Q_{2}

;

P

-ből

P_{3} Q_{2}

P_{1} Q_{3}

P_{2} Q_{1}

-re emelt merőlegeseké

R_{1}

R_{2}

R_{3}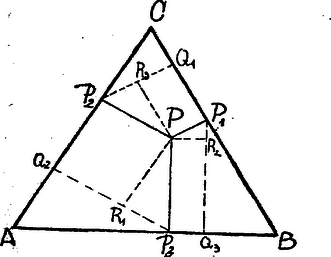

. (53. ábra).

53. ábra

Ekkor

\sqrt[]{3} B P_{1} / 2 = P_{1} Q_{3} = Q_{3} R_{2} + P_{1} R_{2} = P P_{3} + P P_{1} / 2,

hasonlóan

\sqrt[]{3} C P_{2} / 2 = P P_{1} + P P_{2} / 2

és

\sqrt[]{3} A P_{3} / 2 = P P_{2} + P P_{3} / 2

.
Ezeket összeadva:

\begin{matrix} (\sqrt[]{3} / 2) (B P_{1} + C P_{2} + A P_{3}) & = P P_{1} + P P_{2} + P P_{3} + (P P_{1} + P P_{2} + P P_{3}) / 2 \\ = \frac{3}{2} (P P_{1} + P P_{2} + P P_{3}) = (3 / 2) (\sqrt[]{3} / 2) a \\ vagyis B P_{1} + C P_{2} + A P_{3} & = \frac{3}{2} a . \end{matrix}

Gacsályi Sándor (Debreceni gyak. gimn. VIII. o.)