Feladat: C.290 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1993/január, 27 - 28. oldal  PDF  |  MathML 
Témakör(ök): Magasságvonal, A háromszögek nevezetes pontjai, Húrnégyszögek, C gyakorlat
Hivatkozás(ok):Feladatok: 1992/május: C.290

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ABC háromszögben legyen α=60∘,β=59,5∘,γ=60,5∘, a H1=A1B1C1 talpponti háromszögben A1 az A, B1 a B, C1 a C magasságvonal talppontja és M a magasságpont.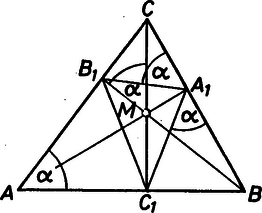

 
 

Könnyen látható, hogy az A1MC1B, B1MA1C, C1MB1A négyszögek húrnégyszögek, mindegyikben 2-2 szemben fekvő szög derékszög. (Tudjuk, hogy az ABC háromszög hegyesszögű és M a háromszög belsejében van, ezt ki is használjuk a bizonyítás során.)
Az AB1MC1 húrnégyszög voltából következik, hogy B1MC∢=B1AC1∢=α, a B1MA1C húrnégyszögben B1A1C∢=B1MC∢=α, ugyanazon ívhez tartozó kerületi szögek; hasonlóan C1A1B∢=α. Ebből következik, hogy a H1 talpponti háromszögben B1A1C1∢=180∘-2α. Mivel a háromszögben nincs kitüntetett csúcs vagy oldal, ezért ugyanígy C1B1A1∢=180∘-2β és A1C1B1∢=180-2γ.
A talpponti háromszögek szögeire tehát a következő sorozatot kapjuk:
H1-ben α1=180∘-2⋅60∘=60∘, β1=180∘-2⋅59,5∘=61∘, γ1=180∘-2⋅60,5∘=59∘ és így tovább, a H2,H3,... talpponti háromszögekben az egyik szög mindig 60∘, a másik két szögre
H2:β2=58∘,γ2=62∘,H3:β3=64∘,γ3=56∘,
H4:β4=52∘,γ4=68∘,H5:β5=76∘,γ5=44∘,
H6:β6=28∘,γ6=92∘.

Tehát a hatodik talpponti háromszög az első tompaszögű háromszög a sorozatban.