Kezdőlap


Feladat:	C.279	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1992/december, 450 - 451. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Síkgeometriai számítások trigonometria nélkül háromszögekben, Koszinusztétel alkalmazása, C gyakorlat
Hivatkozás(ok):	Feladatok: 1992/február: C.279

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az ábra jelölései szerint a $α < β < γ$ . Írjuk fel a legkisebb és legnagyobb szögre a koszinusz-tételt: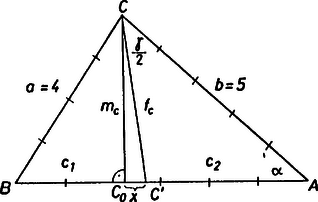

\begin{matrix} cos α = \frac{6^{2} + 5^{2} - 4^{2}}{2 \cdot 5 \cdot 6} = \frac{3}{4}, \end{matrix}

\begin{matrix} cos γ = \frac{4^{2} + 5^{2} - 6^{2}}{2 \cdot 4 \cdot 5} = \frac{1}{8} . \end{matrix}

Azt szeretnénk bizonyítani, hogy

2 α = γ

. A szögek helyett hasonlítsuk össze a szögek koszinuszait:

\begin{matrix} cos 2 α = 2 cos^{2} α - 1 = 2 (\frac{3}{4})^{2} - 1 = \frac{1}{8}, \end{matrix}

s ez valóban egyenlő

cos γ

-val. Mivel hegyesszögekről van szó (mindegyik koszinusz érték pozitív), ezért ebből valóban

2 α = γ

következik.

II. megoldás. Legyen az

A B = c = 6

oldallal szemben fekvő

C

csúcsból induló

f_{c}

szögfelező és

m_{c}

magasság talppontja

C'

, illetve

C_{0}

, továbbá

C' C_{0} = x .

Azt fogjuk elemi úton belátni, hogy az

A C C'

háromszög egyenlő szárú:

f_{c} = C' A

α = \frac{γ}{2}

. Mivel

a < b

, ezért

C_{0}

B C'

szakaszon van.
A szögfelező-tétel szerint

c_{2} = C' A = \frac{b}{a + b} \cdot c = \frac{10}{3}

c_{1} = C' B = \frac{a}{a + b} \cdot c = \frac{8}{3}

egység.
A Pitagorasz-tétel alkalmazásával

m_{c}^{2} = a^{2} - B C_{0}^{2} = a^{2} - {(c_{1} - x)}^{2} = f_{c}^{2} - x^{2}

, azaz

a^{2} = f_{c}^{2} + c_{1}^{2} - 2 c_{1} x

, és hasonlóan

b^{2} = f_{c}^{2} + c_{2}^{2} + 2 c_{2} x

. Az elsőt

c_{2}

-vel, a másodikat

c_{1}

-gyel szorozva és összeadva

x

kiesik:

\begin{matrix} a^{2} c_{2} + b^{2} c_{1} & = (f_{c}^{2} + c_{1} c_{2}) (c_{1} + c_{2}), és \\ f_{c}^{2} & = \frac{a^{2} c_{2} + b^{2} c_{1}}{c} - c_{1} c_{2} = 20 - \frac{80}{9} = \frac{100}{9}, \end{matrix}

tehát valóban

f_{c} = \frac{10}{3} = c_{2}

Megjegyzések 1.

c_{1}

és

c_{2}

betűs kifejezéseivel ezt a szép összefüggést kapjuk:

\begin{matrix} f_{c}^{2} = a b - c_{1} c_{2} . \end{matrix}

2. Tulajdonképpen az ún. Stewart-tételt alkalmaztuk speciális esetben, amely szerint az

A B

szakasz tetszőleges

D

belső pontjára

\begin{matrix} A C^{2} \cdot D B + B C^{2} \cdot D A - D C^{2} \cdot A B = D A \cdot D B \cdot A B \end{matrix}

(Függvénytáblázat, 322.3 összefüggés).