Kezdőlap


Feladat:	C.240	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1992/november, 389 - 390. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Négyzetek, Szögfüggvények, síkgeometriai számítások, C gyakorlat
Hivatkozás(ok):	Feladatok: 1991/január: C.240

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel a két idom területe egyenlő, a kör nem lehet teljes egészében a négyzet belsejében, lesznek tehát ,,kilógó'' részei. A területek egyenlőségéből az is következik, hogy a kilógó és le nem fedett részek területösszege egyenlő.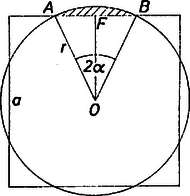

Próbáljuk meghatározni ezen kilógó részek területeinek összegét. Jelöljük a négyzet oldalát

a

-val, a kör sugarát

r

-rel, középpontját (mely egyben a négyzet középpontja is)

O

-val.
A bevonalkázott körszelet területét megkapjuk, ha az

O A B

körcikk területéből kivonjuk az

O A B

háromszög területét. Mindkettőhöz jó lenne ismerni az

A B

ívhez tartozó

2 α

középponti szöget. Az

O F B

háromszögből

cos α = \frac{a}{2 r}

; mivel

a^{2} = r^{2} π

, azért

a = r \sqrt[]{π}

és így

cos α = \frac{\sqrt[]{π}}{2} \approx 0, 8862

, ahonnan

2 α \approx 55, 194^{\circ}

.
Ezt felhasználva

\begin{matrix} T_{szelet} = T_{körcikk} - T_{háromszög} = \frac{r^{2} π 2 α}{360^{\circ}} - \frac{r^{2} sin 2 α}{2} = \\ = \frac{r^{2}}{2} (\frac{π \cdot 55, 194^{\circ}}{180^{\circ}} - sin 55, 194^{\circ}) = r^{2} \cdot 0, 0711 . \end{matrix}

A négy körszelet területének összege megadja a le nem fedett részt, s ezt a kör területéből levonva kapjuk a lefedett rész területét:

\begin{matrix} T_{lefedett} = r^{2} (π - 4 \cdot 0, 0711) = r^{2} \cdot 2, 8572, \end{matrix}

s ez a négyzet területének a

91 %

-a.