Kezdőlap


Feladat:	C.212	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Erős Krisztina
Füzet:	1990/október, 313 - 314. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Beírt gömb, Kocka, Térgeometriai számítások trigonometria nélkül, Koszinusztétel alkalmazása, C gyakorlat
Hivatkozás(ok):	Feladatok: 1990/március: C.212

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A távolságok arányán nem változtat, ha a kocka élét 2 egységnyinek választjuk. Ekkor a beírt gömb sugara 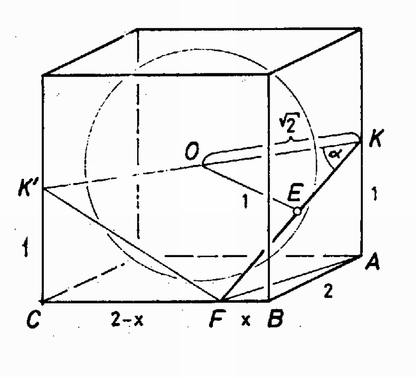$R = 1$ egység.
Jelöljük a kocka három csúcsát $A$ , $B$ , $C$ ,-vel (az ábra szerint), a gömb középpontját $O$ -val. Ha a kockát elmetsszük a $K$ ponton átmenő, alapsíkjával párhuzamos síkkal, a kapott négyzet tartalmazza a gömb középpontját, $O$ -t, és a gömb és a kocka középpontos szimmetriája miatt $K K'$ a négyzet átlója, így hossza $2 \sqrt[]{2}$ .

Mivel az érintési pontban húzott sugár mindig merőleges az érintőre, ezért a

K O E

háromszög derékszögű, így

\begin{matrix} K O = \sqrt[]{2}, O E = R = 1, sin O K E ∢ = sin α = \frac{\sqrt[]{2}}{2}, \end{matrix}

azaz

\begin{matrix} α = 45^{\circ}, így K E = 1. \end{matrix}

Ezután számítsuk ki a

K F

távolságot; legyen

B F = x

.
Az

A B F

derékszögű háromszögből

\begin{matrix} A F^{2} = x^{2} + 2^{2}, \end{matrix}

K A F

derékszögű háromszögből pedig

\begin{matrix} K F^{2} = A F^{2} + A K^{2} = x^{2} + 2^{2} + 1^{2} = x^{2} + 5. \end{matrix}

F C K'

derékszögű háromszögből

\begin{matrix} F K'^{2} = {(2 - x)}^{2} + 1^{2} = 5 - 4 x + x^{2} . \end{matrix}

Végül az

F K' K

háromszögben a koszinusztétel szerint

\begin{matrix} K' F^{2} = F K^{2} + K K'^{2} - 2 F K \cdot K K' cos 45^{\circ} . \end{matrix}

Behelyettesítve az előbb kapott értékeket:

\begin{matrix} 5 - 4 x + x^{2} = x^{2} + 5 + {(2 \sqrt[]{2})}^{2} - 2 \cdot 2 \sqrt[]{2} \cdot \sqrt[]{x^{2} + 5} \cdot \frac{\sqrt[]{2}}{2} . \end{matrix}

A műveleteket és összevonásokat elvégezve

\begin{matrix} x + 2 = \sqrt[]{5 + x^{2}}, \end{matrix}

négyzetreemelve

\begin{matrix} x = B F = \frac{1}{4} . \end{matrix}

Innen

K F = \sqrt[]{x^{2} + 5} = \frac{9}{4}

E F = \frac{5}{4}

, tehát a keresett arányra

\begin{matrix} K E : E F = 1 : \frac{5}{4} = 4 : 5 \end{matrix}

adódik.

Erős Krisztina (Dabas, Táncsics M. Gimn., IV o. t.)
dolgozata alapján