Feladat: 2016. évi Nemzetközi Fizika Diákolimpia 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 2016/október, 425 - 428. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Fizika Diákolimpia, Merev testek dinamikája, Mozgásegyenletek gyorsuló koordináta-rendszerekben, Pontrendszer impulzusnyomatéka (perdülete)
Hivatkozás(ok):Feladatok megoldásai: 2016/november: 2016. évi Nemzetközi Fizika Diákolimpia 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Két mechanikai probléma (összesen 10 pont).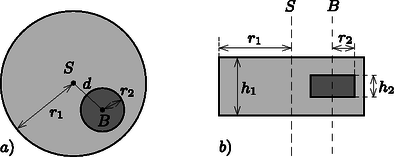
A rész. Elrejtett korong (3,5 pont)
Tekintsünk egy tömör, fából készült, r1 sugarú és h1 vastagságú hengert. A fahenger belsejében valahol a fa anyaga helyett egy r2 sugarú és h2 vastagságú fémkorong található. A fémkorong úgy helyezkedik el, hogy B szimmetriatengelye párhuzamos a fahenger S tengelyével, és ugyanakkora távolságra van a fahenger alsó és felső alaplapjától. Jelöljük S és B távolságát d-vel! A fa sűrűsége ϱ1, a fém sűrűsége pedig ϱ2>ϱ1. A fahenger és a fémkorong össztömege M.
Ebben a részben a fahengert a földre helyezzük, így jobbra és balra szabadon tud gördülni. Az elrendezés oldal- és felülnézetben az 1. ábrán látható.


 

1. ábra. a) oldalnézet; b) felülnézet
 

Ebben a feladatban a fémkorong méretét és helyét kell meghatározni.
A következőkben, ha a választ az ismert mennyiségekkel kell kifejeznünk, mindig az alábbiakat tekinthetjük ismertnek:
r1,h1,ϱ1,ϱ2   és  M.(1)

A cél r2, h2 és d meghatározása indirekt méréseken keresztül.
Jelöljük b-vel a teljes rendszer C tömegközéppontjának és a fahenger S szimmetriatengelyének távolságát! Ennek a távolságnak a meghatározásához a következő kísérletet tervezzük: a fahengert vízszintes alapra helyezzük úgy, hogy stabil egyensúlyban legyen. Az alapot lassan megdöntjük α szöggel (2. ábra). A tapadási súrlódás miatt a fahenger csúszás nélkül gördülhet. A henger egy kicsit lejjebb gördül a lejtőn, de végül valamekkora φ szögelfordulás után a stabil egyensúlyi helyzetben megáll. A φ szöget megmérhetjük.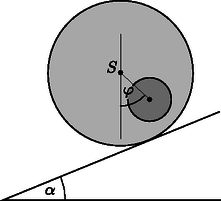


 

2. ábra. A henger a lejtőn
 

A.1. Fejezzük ki b-t az (1)-ben felsorolt mennyiségek, a φ szög és az α hajlásszög függvényében! (0,8 pont)
Mostantól kezdve b értékét ismertnek tekinthetjük.
A továbbiakban szeretnénk megmérni a rendszer ΘS tehetetlenségi nyomatékát az S szimmetriatengelyre vonatkoztatva. Ehhez egy mereven rögzített rúddal felfüggesztjük a fahengert a szimmetriatengelyénél. Ezután az egyensúlyi helyzetéből kicsiny φ szöggel kitérítjük, majd elengedjük (3. ábra). Azt találjuk, hogy φ periodikusan változik T periódusidővel.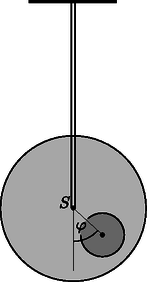


 

3. ábra. A felfüggesztett rendszer
 

A.2. Határozzuk meg φ mozgásegyenletét! Fejezzük ki a hengernek az S szimmetriatengelyére vonatkoztatott ΘS tehetetlenségi nyomatékát T, b és az (1)-ben felsorolt, ismert mennyiségek segítségével! Feltételezhetjük, hogy az egyensúlyi helyzettől való kitérés kicsi, így φ a mozgás során mindvégig igen kicsiny marad. (0,5 pont)
Az A.1. és A.2. részfeladatok mérései alapján szeretnénk meghatározni a fahengerben található fémkorong geometriáját és elhelyezkedését.
A.3. Fejezzük ki a d távolságot b és az (1)-ben szereplő mennyiségek segítségével. A formulában az r2 és h2 mennyiségeket is használhatjuk, hiszen ezeket az A.5. pontban meg fogjuk határozni. (0,4 pont)
A.4. Fejezzük ki az ΘS tehetetlenségi nyomatékot b és az (1)-ben szereplő, ismert mennyiségek segítségével. A formulában az r2 és h2 mennyiségeket is használhatjuk, hiszen ezeket az A.5. pontban meg fogjuk határozni. (0,7 pont)
A.5. A fenti eredményeket felhasználva fejezzük ki h2 és r2 értékét b, T és (1)-ben szereplő, ismert mennyiségek segítségével. A h2 mennyiséget kifejezhetjük r2-vel is. (1,1 pont)
 
B rész. Forgó űrállomás (6,5 pont)
Alice egy űrállomáson lakó űrhajós. Az űrállomás egy óriási, R sugarú kerék, amely a tengelye körül forog, így biztosítva a mesterséges gravitációt az asztronauták számára. Az űrhajósok a kerék peremének belső oldalán élnek. Az űrállomás gravitációs vonzása és a padló görbültsége elhanyagolható.
 
B.1. Mekkora ω0 szögsebességgel forog az űrállomás, ha az űrhajósok ugyanakkora gF gravitációs gyorsulást éreznek, mint a Föld felszínén? (0,5 pont)
Alice és űrhajós barátja, Bob vitatkoznak. Bob nem hiszi el, hogy valóban egy űrállomáson élnek, szerinte ténylegesen a Földön tartózkodnak. Alice fizikai módszerrel szeretné bebizonyítani Bobnak, hogy egy forgó űrállomáson élnek. Ezért egy m tömegű testet rögzít egy k rugóállandójú rugó végére, majd rezgésbe hozza. A test csak függőleges irányban rezeghet, vízszintesen nem tud mozogni.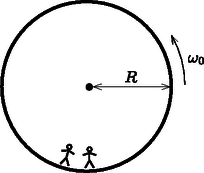
 
B.2. Feltételezve, hogy a Földön a gravitációs gyorsulás állandó gF, mekkorának mérné a rezgés ωF körfrekvenciáját egy Földön lévő személy? (0,2 pont)


 

4. ábra. Az űrállomás
 

 
B.3. Mekkora ω körfrekvenciát mér Alice az űrállomáson? (0,6 pont)
Alice meg van győződve arról, hogy a kísérlete bizonyíték arra, hogy egy forgó űrállomáson élnek. Bob szkeptikus marad. Szerinte ha a gravitációs tér Föld felszíne feletti változását is figyelembe vesszük, annak hasonló hatása van. A továbbiakban azt vizsgáljuk, igaza van-e Bobnak.
 
B.4. Fejezzük ki a gF(h) gravitációs gyorsulást kicsiny h magasságban a Föld felszíne fölött, és számítsuk ki a rezgő test ωF˜ körfrekvenciáját (elég a lineáris közelítés). A Föld sugarát jelölje RF. A Föld forgását figyelmen kívül hagyhatjuk. (0,8 pont)
Alice azt találja, hogy ezen az űrállomáson a rezgő test valóban a Bob által jósolt frekvenciával rezeg.
 
B.5. Mekkora az űrállomás R sugara, ha a rezgés ω körfrekvenciája megegyezik a Földön mérhető ωF˜ körfrekvenciával? A választ RF segítségével adjuk meg. (0,3 pont)
Bob makacsságán feldühödve Alice egy új kísérlettel áll elő saját igazának bizonyítására. Ezért felmászik az űrállomás padlója fölé H magasságba egy toronyra, és elejt egy testet. Ez a kísérlet értelmezhető a forgó vonatkoztatási rendszerben éppúgy, mint az inerciarendszerben.
Egy egyenletesen forgó vonatkoztatási rendszerben az űrhajós egy fiktív FC erőt tapasztal, amit Coriolis-erőnek nevezünk. Az állandó ω0 szögsebességgel forgó rendszerben v sebességgel mozgó, m tömegű testre ható FC Coriolis-erőt a következő összefüggés adja meg:
FC=2mv×ω0.
Használható a skaláris mennyiségekre vonatkozó
FC=2mvω0sinφ
alak, ahol φ a sebességvektor és a forgástengely közötti szög. Az erő merőleges mind a v sebességvektorra, mind pedig a forgástengelyre. Az erő előjele a jobbkéz-szabály alapján határozható meg, de ez az előjel a következőkben szabadon választható.
B.6. Számítsuk ki a test vx vízszintes sebességét és a vízszintes dx elmozdulását (a torony aljához képest, a toronyra merőleges irányban) a padlóra érés pillanatában. Feltehetjük, hogy a torony H magassága kicsiny, így az űrhajósok által mért gyorsulás az esés alatt állandó. Feltételezhető továbbá, hogy dx≪H. (1,1 pont)
Hogy jobb eredményt kapjon, Alice úgy dönt, hogy a kísérletet egy, a korábbinál sokkal magasabb toronyról is elvégzi. Meglepetésére a test a torony aljánál éri el a padlót, azaz dx=0.
B.7. Határozzuk meg a torony magasságának alsó korlátját, amelyre dx=0 lehetséges. (1,3 pont)
Alice szeretne még egy utolsó kísérletet tenni Bob meggyőzésére. A rugós rendszert szeretné használni a Coriolis-erő hatásának szemléltetésére. Ezért megváltoztatja az eredeti elrendezést: a rugót egy olyan gyűrűhöz rögzíti, amely szabadon és súrlódásmentesen csúszhat az x irányban egy vízszintes rúdon. A rugó maga az y irányban rezeg. A rúd párhuzamos a talajjal és merőleges az űrállomás forgástengelyére. Az x-y sík tehát merőleges a forgástengelyre, az y irány pedig egyenesen az űrállomás forgástengelye felé mutat.
B.8. Alice a testet az x=0, y=0 egyensúlyi állapotából d távolsággal kitéríti lefelé, majd elengedi (lásd az 5. ábrát).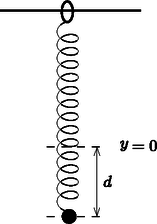


 

5. ábra. Az elrendezés
 

(i) Fejezzük ki az x(t) és y(t) mennyiségeket. Feltehetjük, hogy ω0d kicsi, és elhanyagolhatjuk az y irányú Coriolis-erőt.
(ii) Vázoljuk fel az (x(t),y(t)) pályát, és jelöljük minden fontos tulajdonságát, mint pl. az amplitúdóját. (Összesen 1,7 pont)
Alice és Bob folytatja vitáját ...