Feladat: 2015. évi Nemzetközi Fizika Diákolimpia 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 2015/október, 428 - 430. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Fizika Diákolimpia, Egyéb feladatok, Young-féle (kétréses) interferencia, Fermat-elv, de Broglie-hipotézis
Hivatkozás(ok):Feladatok megoldásai: 2015/november: 2015. évi Nemzetközi Fizika Diákolimpia 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2. feladat. A szélsőértékelv (összesen 10 pont).

 

A rész. Szélsőértékelv a mechanikában
Tekintsünk egy vízszintes, súrlódásmentes x-y síkot (1. ábra). A síkot az x=x1 egyenlettel megadott AB egyenes két, I és II jelű tartományra osztja. Egy m tömegű, pontszerű test helyzeti energiája az I-es tartományban V=0, míg a II-es tartományban V=V0. A részecskét az O origóból v1 sebességgel indítjuk el egy, az x tengellyel ϑ1 szöget bezáró egyenes mentén. A II-es tartományban lévő P pontot v2 sebességgel éri el egy, az x tengellyel ϑ2 szöget bezáró egyenes mentén.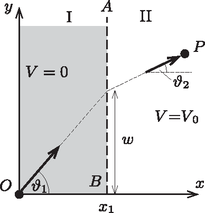


 

1. ábra
 

A gravitációt és a relativisztikus hatásokat a feladat minden részében elhanyagolhatjuk.

A.1. Fejezzük ki v2-t az m, v1 és V0 mennyiségek segítségével! (0,2 pont)
A.2. Adjuk meg v2-t v1, ϑ1 és ϑ2 segítségével! (0,3 pont)
Definiálunk egy (hatásnak nevezett) A=m∫v(s)ds mennyiséget, ahol ds a v(s) sebességgel mozgó m tömegű részecske ,,infinitezimálisan kicsi'' elmozdulása a pályája mentén. Az integrálást a pályagörbe mentén kell elvégezni.
Példaként, ha egy részecske állandó v sebességgel mozog egy R sugarú körpályán, akkor az A hatás 1 fordulat alatt 2πmRv lesz.
Ha a részecske E energiája állandó, akkor megmutatható, hogy két rögzített végpont között az összes lehetséges pálya közül a részecske ténylegesen azon a pályán fog mozogni, amelyen kiszámítva az A hatásnak szélsőértéke (minimuma vagy maximuma) van. Történeti okokból ezt a szélsőértékelvet a legkisebb hatás elvének (LHE) nevezik.
A.3. A LHE-ből következik, hogy ha egy részecske olyan tartományban mozog, ahol a helyzeti energia állandó, a pályája a két rögzített pont közötti egyenes szakasz lesz. Legyenek az 1. ábrán látható O és P rögzített pontok koordinátái (0,0), illetve (x0,y0), továbbá annak a határpontnak a koordinátái, ahol a részecske az I-es tartományból átmegy a II-esbe, legyenek (x1,w). Fontos, hogy x1 értéke rögzített, és a hatás csak a w koordináta függvénye. Adjuk meg az A(w) hatásfüggvény alakját! Az LHE alapján keressünk kapcsolatot a v1/v2 hányados és a fenti koordináták között! (1,0 pont)
 
B rész. Szélsőértékelv az optikában
Egy fénysugár az n1 törésmutatójú I-es közegből az n2 törésmutatójú II-es közegbe lép át. A két közeget egy x tengellyel párhuzamos egyenes választja el. A fénysugár az y tengellyel az I-es közegben α1, a II-es közegben α2 szöget zár be (2. ábra). A fénysugár útját egy másik szélsőértékelv, a legkisebb idő elvét megfogalmazó Fermat-elv segítségével kapjuk meg.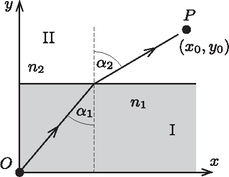


 

2. ábra
 

B.1. Az elv azt mondja ki, hogy két rögzített pont között a fénysugár olyan pályán halad, amelyen a két pont közötti út megtételéhez szükséges időnek szélsőértéke van. Vezessük le a sinα1 és sinα2 közötti összefüggést a Fermat-elv alapján! (0,5 pont)
 

A 3. ábrán (vázlatosan) egy olyan lézersugár menete látható, amely vízszintesen lép be egy cukoroldatba. Az oldatban a cukorkoncentráció ‐ és ennek következtében a törésmutató is ‐ csökken a magassággal.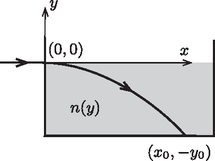


 

3. ábra
 

B.2. Tegyük fel, hogy a törésmutató csak y koordinátától függ, n=n(y). A B.1. részben kapott összefüggés segítségével fejezzük ki a fénysugár pályájának dy/dx meredekségét az n0 és n(y) törésmutatók függvényében, ahol n0 a törésmutató értéke az y=0 helyen! (1,5 pont)
B.3. A lézersugár a (0,0) origóban vízszintesen lép be a cukoroldatba az edény aljához viszonyítva y0 magasságban, ahogy az a 3. ábrán látszik. Legyen n(y)=n0-ky, ahol n0 és k pozitív állandók. Fejezzük ki x-et y és a lézersugár pályáját meghatározó többi mennyiség függvényében! (1,2 pont)
Felhasználható, hogy:
∫1cosϑdϑ=ln(1cosϑ+tgϑ)+állandó,vagy∫dx(x2-1)=ln(x+x2-1)+állandó.


B.4. Határozzuk meg azt az x0 értéket, ahol a fénysugár eléri az edény alját! Legyen: y0=10,0cm; n0=1,50; k=0,050cm-1. (0,8 pont)
 
C rész. A szélsőértékelv és az anyag hullámtermészete
Most a legkisebb hatás elve (LHE) és a mozgó részecske hullámtermészetének kapcsolatát fogjuk tanulmányozni. Ehhez azt feltételezzük, hogy az O-ból P-be haladó részecske minden lehetséges pályát befut, és mi azt a pályát keressük meg, amelyen az interferáló de Broglie-hullámok erősítik egymást.
C.1. A részecske egy infinitezimális kicsi Δs távolsággal elmozdul a pályáján. Fejezzük ki a de Broglie-hullám Δφ fázisváltozását a hatás ΔA megváltozásával és a Planck-állandóval! (0,6 pont)
C.2. Tekintsük újra az A részben szereplő feladatot, ahol a részecske O-ból P-be mozog (4. ábra). Tegyünk egy átlátszatlan lemezt a két tartomány közti AB határvonalra. Ezen egy kicsiny, d szélességű CD nyílás van, melyre teljesül, hogy 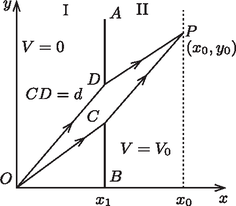d≪(x0-x1) és d≪x1.


 

4. ábra
 

Vegyük fel az OCP és ODP szélső pályákat, úgy, hogy OCP az A részben tárgyalt klasszikus pályán legyen. Határozzuk meg első rendben a két pálya közötti ΔφCD fáziskülönbséget! (1,2 pont)
 
D rész. Anyaghullámok interferenciája
Tekintsünk egy elektronágyút O-ban, amely egy párhuzamosított elektronnyalábot bocsát ki a keskeny F rés irányába. A rés az x=x1 helyen lévő A1B1 átlátszatlan elválasztófalon úgy helyezkedik el, hogy az ernyőn lévő P pont, valamint O és F egy egyenesen legyen (5. ábra). A sebesség az I-es tartományban v1=2,0000⋅107m/s, és ϑ=10,0000∘. A II-es tartományban olyan a potenciál, hogy a sebesség v2=1,0000⋅107m/s. Az x0-x1 távolság 250,00mm. (Az elektronok közötti kölcsönhatást hanyagoljuk el.)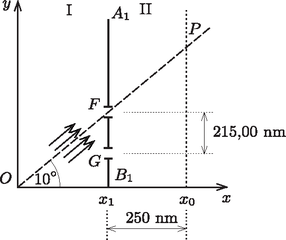


 

5. ábra
 

D.1. Számítsuk ki az elektronágyú U1 gyorsítófeszültségét, ha O-ban az elektronokat nyugalmi helyzetből gyorsítjuk fel! (0,3 pont)
D.2. Az A1B1 elválasztófalon az F rés alatt, attól 215,00 nm távolságra egy másik (G jelű) keskeny rést is létrehozunk. Az F és G réseken át a P pontba érkező de Broglie-hullámok fáziskülönbsége 2πβ. Számítsuk ki β értékét! (0,8 pont)
D.3. Mekkora az a P-től mért legkisebb Δy távolság, ahol nem várható elektron becsapódása az ernyőn? (1,2 pont)
Figyelem! Hasznos lehet a sin(ϑ+Δϑ)≈sinϑ+Δϑcosϑ közelítés.

D.4. A sugár négyzetes keresztmetszete 500nm×500nm, és a mérési összeállítás hossza 2m. Mekkora az a minimális Imin fluxussűrűség (elektron darabszám/egységnyi merőleges felület/egységnyi idő), amely esetében egy adott időpillanatban átlagosan legalább 1 elektron található a mérési összeállításban? (0,4 pont)