Feladat:	2014. évi Nemzetközi Fizika Diákolimpia 3. feladata	Korcsoport: -	Nehézségi fok: nehéz
Füzet:	2014/október, 429 - 431. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Egyéb kinetikus gázelmélet, Szabad úthossz, Egyéb áramkörök
Hivatkozás(ok):	Feladatok megoldásai: 2014/november: 2014. évi Nemzetközi Fizika Diákolimpia 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   3. feladat. A gázkisülés legegyszerűbb modellje (összesen 10 pont). Egy gázon átfolyó elektromos áramot gázkisülésnek nevezik. Sokféle gázkisülés van: a fénycsövekben, a hegesztéshez használt ívkisülés, és a villámokból jól ismert szikrakisülések. A rész. Nem önfenntartó gázkisülés (4,8 pont). A feladatnak ebben a részében az úgynevezett nem önfenntartó gázkisülést tanulmányozzuk. Ahhoz, hogy folyamatos gázkisülés jöjjön létre, egy külső ionizálóra van szükség, amely térfogat- és időegységenként $Z_{\text{ext}}$ darab egyszeresen ionizált ionból és szabad elektronból álló párt hoz létre. Amikor a külső ionizálót bekapcsoljuk, az elektronok és ionok száma nőni kezd. Az elektron- és ionsűrűség határtalan növekedésének a rekombináció szab gátat: ebben a folyamatban egy szabad elektron és egy ion semleges atommá rekombinálódik. A térfogat- és időegységenként lejátszódó rekombinációk $Z_{\text{rek}}$ számát a következő kifejezés adja meg: $\begin{array}{c}{\displaystyle Z_{\text{rek}}=r{n}_{\text{e}}{n}_{\text{i}}\mathrm{,}}\end{array}$ ahol az $r$ állandó az úgynevezett rekombinációs együttható, és $n_{\text{e}}$, illetve $n_{\text{i}}$ az elektron-, illetve ionsűrűséget jelenti. Tegyük fel, hogy a külső ionizálót a $t=0$ pillanatban kapcsoljuk be, és ekkor az elektronok és az ionok kezdeti sűrűsége egyaránt nulla. Ezután az elektronok $n_{\text{e}}\left(t\right)$ sűrűsége a $t$ idő függvényében a következőképp változik: $\begin{array}{c}{\displaystyle n_{\text{e}}\left(t\right)=n_0+a\text{th}\left(bt\right)\mathrm{,}}\end{array}$ ahol $a$ és $b$ állandók, $\text{th}x$ pedig a tangens hiperbolikusz függvény. $A_1$ kérdés (1,8 pont): Határozd meg és fejezd ki $n_0$, $a$, $b$ értékét $Z_{\text{ext}}$ és $r$ függvényében. Tegyük fel, hogy két külső ionizálónk van. Ha csak az egyiket kapcsoljuk be, az elektronsűrűség a gázban $n_{\text{e1}}=12\cdot {10}^{10}{\text{cm}}^{-3}$ egyensúlyi értéket ér el. Ha csak a másikat kapcsoljuk be, akkor viszont az egyensúlyi elektronsűrűség $n_{\text{e2}}=16\cdot {10}^{10}{\text{cm}}^{-3}$. $A_2$ kérdés (0,6 pont): Határozd meg a gázban kialakuló egyensúlyi $n_{\text{e}}$ elektronsűrűséget, ha egyszerre mindkét külső ionizálót bekapcsoljuk. Figyelem! A következőkben feltételezzük, hogy a külső ionizáló hosszú ideje be van kapcsolva, a folyamatok stacionáriussá váltak, és nem függenek az időtől. A töltéshordozók által keltett elektromos teret hagyd teljesen figyelmen kívül. Tegyük fel, hogy a gáz egy csőben van két párhuzamos, $A$ területű vezető lemez között, melyek távolsága egymástól $L\ll \sqrt[]{A}$. A lemezek közé kapcsolt $U$ feszültség elektromos teret hoz létre. Tegyük fel, hogy mindkét fajta töltéshordozó sűrűsége közel állandó a csőben. Tegyük fel, hogy az elektronok (jelöljük e indexszel) és az ionok (jelöljük i indexszel) is ugyanakkora $v$ rendezett sebességre tesznek szert az $E$ elektromos tér hatására: $\begin{array}{c}{\displaystyle v=\beta U\mathrm{,}}\end{array}$ ahol a $\beta$ állandó neve mobilitás. $A_3$ kérdés (1,7 pont): Fejezd ki a csőben folyó $I$ elektromos áramot $U$, $\beta$, $L$, $A$, $Z_{\text{ext}}$, $r$ és az $e$ elemi töltés függvényében. $A_4$ kérdés (0,7 pont): Határozd meg és fejezd ki a gáz ${\varrho }_{\text{gáz}}$ fajlagos ellenállását $\beta$, $L$, $Z_{\text{ext}}$, $r$ és $e$ függvényében kellően kicsi feszültség esetén. B rész. Önfenntartó gázkisülés (5,2 pont). A feladatnak ebben a részében az önfenntartó gázkisüléssel foglalkozunk, és megmutatjuk, hogyan válik a csőben az áram önfenntartóvá. Figyelem! A következő részben a külső ionizálás ugyanazzal a $Z_{\text{ext}}$ ionizációs rátával működik tovább. Hanyagold el a töltéshordozók által keltett elektromos teret, így az elektromos tér homogén a csőben. Ezen kívül a rekombináció is teljesen elhanyagolható. Az önfenntartó gázkisülésben van két fontos folyamat, amit eddig nem vettünk figyelembe. Az első folyamat a szekunder elektronok kibocsátása, a második pedig az elektronlavinák kialakulása. A szekunder elektron kibocsátás akkor történik, ha ionok ütköznek a negatív elektródnak (katód), és a kilökött elektronok a pozitív elektród (anód) felé mozognak. Az egységnyi idő alatt kilökött elektronok ${\dot{N}}_{\text{e}}$ számának és az egységnyi idő alatt a katódba csapódó ionok ${\dot{N}}_{\text{i}}$ számának aránya a szekunder elektron kibocsátási együttható: $\begin{array}{c}{\displaystyle \gamma =\frac{{\dot{N}}_{\text{e}}}{{\dot{N}}_{\text{i}}}\mathrm{.}}\end{array}$ Az elektron-lavinák kialakulását a következőképp magyarázhatjuk. Az elektromos tér felgyorsítja az elektronokat, melyek mozgási energiája elég nagy lesz ahhoz, hogy ütközéskor újabb atomokat ionizáljanak. Ennek következtében jelentősen megnő az anód felé haladó szabad elektronok száma. Ezt a jelenséget az $\alpha$ Townsend-együtthatóval írjuk le, ami megadja az elektronok számának $\text{d}{N}_{\text{e}}$ növekedését miközben $N_{\text{e}}$ elektron áthalad $\Delta \ell$ távolságon: $\begin{array}{c}{\displaystyle \frac{\text{d}{N}_{\text{e}}}{\text{d}\ell }=\alpha N_{\text{e}}\mathrm{.}}\end{array}$ A teljes $I$ áram a cső bármely keresztmetszetén az $I_{\text{i}}\left(x\right)$ ionáramból és az $I_{\text{e}}\left(x\right)$ elektronáramból áll, melyek állandósult állapotban függenek a 5. ábrán látható $x$ koordinátától. Az $I_{\text{e}}\left(x\right)$ elektronáram az $x$ tengely mentén a következőképp változik: 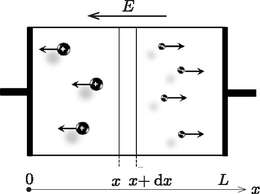$\begin{array}{c}{\displaystyle I_{\text{e}}\left(x\right)=C_1{e}^{A_{1}x}+A_2\mathrm{,}}\end{array}$ ahol $A_1$, $A_2$ és $C_1$ állandók.   5. ábra   $B_1$ kérdés (2 pont): Határozd meg és fejezd ki $A_1$, $A_2$ értékét $Z_{\text{ext}}$, $\alpha$, $e$, $L$ és $A$ függvényében. Az $I_{\text{i}}\left(x\right)$ ionáram az $x$ tengely mentén a következő kifejezés szerint változik: $\begin{array}{c}{\displaystyle I_{\text{i}}\left(x\right)=C_2{e}^{B_{1}x}+B_2\mathrm{,}}\end{array}$ ahol $B_1$, $B_2$ és $C_2$ állandók. $B_2$ kérdés (0,6 pont): Határozd meg és fejezd ki $B_1$, $B_2$ értékét $Z_{\text{ext}}$, $\alpha$, $e$, $L$, $A$ és $C_1$ függvényében. $B_3$ kérdés (0,3 pont): Add meg az $I_{\text{i}}\left(x\right)$-re vonatkozó peremfeltételt, ha $x=L$. $B_4$ kérdés (0,6 pont): Add meg az $I_{\text{i}}\left(x\right)$-re és $I_{\text{i}}\left(x\right)$-re vonatkozó peremfeltételt, ha $x=0$. $B_5$ kérdés (1,2 pont): Határozd meg és fejezd ki az $I$ teljes áram értékét $Z_{\text{ext}}$, $\alpha$, $\gamma$, $e$, $L$ és $A$ függvényében. Tedd fel, hogy ez az érték véges marad. Legyen az $\alpha$ Townsend-együttható állandó. Ha a cső hossza nagyobbá válik, mint egy kritikus érték, azaz $L>L_{\text{krit}}$, a külső ionizálás kikapcsolható, és a kisülés önfenntartóvá válik. $B_6$ kérdés (0,5 pont): Határozd meg és fejezd ki $L_{\text{krit}}$ értékét $Z_{\text{ext}}$, $\alpha$, $\gamma$, $e$, $L$ és $A$ függvényében.