Kezdőlap


Feladat:	2006. évi Eötvös fizikaverseny 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Kitűző(k):	Varga István
Füzet:	2007/március, 172 - 176. oldal		PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén), Áramvezetőre ható erő

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Négyzet alakú, rövidre zárt lapos tekercs anyaga szupravezető (ellenállása elhanyagolható). A négyzet oldalélei $l$ hosszúak, egy-egy oldalának tömege $m$ . A tekercs, amelynek induktivitása $L$ , súrlódásmentesen elfordulhat a négyzet alsó, vízszintes oldala körül.
Kezdetben a tekercs függőlegesen, labilis egyensúlyi helyzetben áll a földi nehézségi erőtérben. Ezután egy olyan homogén mágneses mezőt alkalmazunk, hogy a tekercsre ható $B$ mágneses indukció vektor nagysága állandó, iránya függőleges legyen. Ekkor a tekercsben nem folyik áram.
Ezután a tekercs felső végét kicsiny $v_{0}$ sebességgel meglökjük. Körbefordul-e a tekercs, vagy ha nem, akkor milyen határok között fog mozogni?

Megoldás. Az alapvető összefüggés, melyből ennek a feladatnak a megoldásánál kiindulhatunk, a dinamikának az az alaptörvénye, amely merev testeknek rögzített tengely körüli forgására vonatkozik:

\begin{matrix} Θ β = \sum M, \end{matrix}

vagyis a test

Θ

tehetetlenségi nyomatékának és

β

szöggyorsulásának szorzata a testre ható erők forgatónyomatékainak összegével egyenlő.
A feladat szempontjából lényegtelen, hogy a ,,lapos tekercs'' hány menetes, ezért a továbbiakban azt egy keretnek (1 menetes tekercsnek) tekintjük (3. ábra). Az ábrán felrajzoltuk azokat az erőket, amelyek akkor hatnak a keretre, amikor az már

α

szögben kilendült eredeti függőleges helyzetéből. Az oldalakra ható

m g

nehézségi erő tovább akarja forgatni a keretet, a felső oldalra ható

B I l

erő vízszintes irányú (a többi oldalon ható mágneses erőknek nincs forgatónyomatéka, így ezekkel nem kell törődnünk). Mivel a keretben folyó áram az elektromágneses indukció miatt lép fel, ezért ‐ Lenz törvénye szerint ‐ a felső oldalon ható erő visszafelé akarja forgatni a keretet. A hozzá tartozó erőkar

l cos α

nagyságú, tehát:

\begin{matrix} Θ β = m g l sin α + 2 m g \frac{l}{2} sin α - B I l \cdot l cos α . \end{matrix}

Ebben az egyenletben

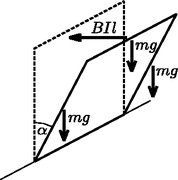\begin{matrix} Θ = m l^{2} + 2 \cdot \frac{1}{3} m l^{2} = \frac{5}{3} m l^{2} . \end{matrix}

3. ábra

Hogyan határozhatjuk meg az

I

indukált áram nagyságát? A tekercsben most kétféle okból lép fel indukált feszültség. Az egyik ok, hogy vezető mozog a mágneses térben. Ennek megfelelően az indukált feszültség nagysága Neumann törvénye szerint

\begin{matrix} U_{1} = B l v cos α . \end{matrix}

A másik ok az, hogy az

L

induktivitású tekercsben változik az áram, ezért a fellépő önindukciós feszültség

\begin{matrix} U_{2} = - L \frac{Δ I}{Δ t} . \end{matrix}

A kettő előjeles összege adja

I R

-et a lassan változó áramokra is igaz Kirchhoff-féle huroktörvény szerint. Mivel a tekercs anyaga most szupravezető, ezért

R = 0

, tehát

\begin{matrix} B l \frac{Δ s}{Δ t} cos α - L \frac{Δ I}{Δ t} = 0. \end{matrix}

Ha ebből akarjuk

I

-t kifejezni, akkor (

Δ s = l Δ α

behelyettesítése után) integrálnunk kell az egyenletet. Ennek a matematikai műveletnek a megkerülésével is eljuthatunk azonban a helyes összefüggéshez, ha azt vesszük figyelembe, hogy a keret

A = l^{2}

nagyságú keresztmetszetén áthaladó teljes fluxus (amely a külső mágneses tértől származó fluxus és az önindukciós fluxus összege) állandó kell maradjon:

\begin{matrix} B A sin α - L I = állandó . \end{matrix}

Az állandó értéke

L I_{0} = 0,

hiszen a kezdeti (

α = 0

-hoz tartozó)

I_{0}

áram nulla volt. A fenti egyenletből már kifejezhetjük

I

-t:

\begin{matrix} I = \frac{B l^{2}}{L} \cdot sin α . \end{matrix}

B

l

és

L

adott állandók,

I

tehát

sin α

-val arányos mennyiség. Erre a felismerésre még szükségünk lesz, de mielőtt diszkutálni kezdjük a feladatot, gondoljuk át, milyen fizikai törvényt, összefüggést használhatunk még fel a megoldás során!
Szükségünk lehet energetikai meggondolásra. Írjuk fel a munkatételt (a kinetikai energia tételét)! Eszerint

\begin{matrix} Δ E_{mozg.} = \sum W, \end{matrix}

vagyis

\begin{matrix} \frac{1}{2} Θ ω^{2} - \frac{1}{2} Θ ω_{0}^{2} = m g l (1 - cos α) + 2 m g \frac{l}{2} (1 - cos α) - \frac{1}{2} L I^{2} . \end{matrix}

(A jobb oldalon az utolsó tag az önindukcióból származó

U_{ind.} = - L \cdot Δ I / Δ t

feszültség

U_{ind.} I Δ t

munkavégzését fejezi ki.) A fenti összefüggéshez ,,energiatételként'' is eljuthatunk, amely szerint

\begin{matrix} \sum E = állandó, vagyis \sum E_{kezdeti} = \sum E_{α}, \end{matrix}

tehát

\begin{matrix} \frac{1}{2} Θ ω_{0}^{2} = \frac{1}{2} Θ ω^{2} - 2 m g l (1 - cos α) + \frac{1}{2} L I^{2} . \end{matrix}

Most kezdjünk a diszkusszióhoz! Vizsgáljuk meg először azt az esetet, amikor a meglökéssel adott

v_{0}

sebesség kicsi, és emiatt a kilendülési

α

szög is olyan kicsi, hogy megengedhető a

sin α \approx α

és

cos α \approx 1

közelítés. Ekkor a forgómozgás dinamikai egyenlete:

\begin{matrix} Θ β = 2 m g l α - B I l^{2}, \end{matrix}

az áram pedig így függ

α

-tól:

\begin{matrix} I = \frac{B l^{2}}{L} α . \end{matrix}

Behelyettesítve

I

kifejezését a dinamikai egyenletbe:

\begin{matrix} Θ β = 2 m g l α - \frac{B^{2} l^{4}}{L} α = - (\frac{B^{2} l^{4}}{L} - 2 m g l) α . \end{matrix}

Látjuk, hogy a

β

szöggyorsulás az

α

szögkitéréssel arányosnak adódik. Tudjuk, hogy a

β = - Ω^{2} α

típusú összefüggés harmonikus rezgésre vezet, mégpedig olyanra, aminek

Ω

a körfrekvenciája, vagyis a feltételezett esetben olyan harmonikus rezgő ,,lengésbe'' kezd a tekercs, amelynek periódusideje

T = \frac{2 π}{Ω}

lesz.

Θ = \frac{5}{3} m l^{2}

behelyettesítése után kapjuk:

\begin{matrix} T = 2 π \sqrt[]{\frac{5}{3 (\frac{B^{2} l^{2}}{m L} - 2 \frac{g}{l})}} . \end{matrix}

A kilendülés maximális szöge:

\begin{matrix} α_{{max}_{}^{}} = \frac{v_{0}}{Ω l} = \frac{v_{0} T}{2 π l} . \end{matrix}

A periódusidőre kapott kifejezést figyelmesen megvizsgálva felvetődik a kérdés: nem állhat ott a gyökjel alatt negatív szám? Mi van akkor, ha

\frac{B^{2} l^{2}}{m L} < 2 \frac{g}{l} ?

Elég gyenge mágneses tér, kicsiny

B

esetén ez bizonyára előfordulhat! Visszatérve a dinamikai egyenlethez, azt látjuk, hogy ilyenkor

β

0 < α < 180^{\circ}

intervallumon mindig pozitív marad, akármilyen kicsiny is a kezdeti

v_{0}

érték. Sejthető, hogy ilyenkor nem lesz maximális kilendülési szög, hanem a lebillenő tekercs egyre nagyobb szögsebességgel forog, s végül átlendül, átfordul a legalsó helyzetén és szépen visszatér a

v_{0} / l

szögsebességű kezdőállapotba. Vagyis folyton-folyvást forogni fog, sose áll meg, mert szupravezető, s így nem disszipálódhat az energia. (Persze még kisugárzódhat, ez további meggondolásokat igényel

...

)
Vizsgáljuk meg most azt az esetet, amikor

v_{0}

akármekkora lehet! Vajon milyen feltételek teljesülése esetén áll meg és fordul vissza valahonnan a tekercs, és mikor fog folyamatosan egyirányban forogni?
Mi a megállás feltétele? Ehhez szükségünk lesz az energetikai meggondolásra:

\begin{matrix} \frac{1}{2} Θ ω^{2} = \frac{1}{2} Θ ω_{0}^{2} + 2 m g l (1 - cos α) - \frac{1}{2} L I^{2} . \end{matrix}

Keressük a megálláshoz,

ω = 0

-hoz tartozó

α

szöget:

\begin{matrix} 0 = \frac{1}{2} Θ ω_{0}^{2} + 2 m g l (1 - cos α) - \frac{1}{2} L I^{2} . \end{matrix}

Írjuk be ide is az áram szögfüggését:

\begin{matrix} 0 = \frac{1}{2} Θ ω_{0}^{2} + 2 m g l (1 - cos α) - \frac{1}{2} \frac{B^{2} l^{4}}{L} sin^{2} α . \end{matrix}

Felhasználva, hogy

sin^{2} α = 1 - cos^{2} α

, jól látszik, hogy

cos α

-ra kaptunk egy másodfokú egyenletet, ami lényegében ilyen alakú:

a cos^{2} α + b cos α + c = 0

, és aminek megoldása:

\begin{matrix} cos α = \frac{- b \pm \sqrt[]{b^{2} - 4 a c}}{2 a} . \end{matrix}

A meglökött tekercs tehát akkor áll meg valahol, ha a fenti másodfokú egyenletnek van valós megoldása, és ez a megoldás abszolút értékben nem nagyobb 1-nél (hiszen egy szög koszinuszáról van szó).
Teljesülnie kell tehát a következő két feltételnek:

\begin{matrix} b^{2} - 4 a c \geq 0, & (1) \\ | \frac{- b \pm \sqrt[]{b^{2} - 4 a c}}{2 a} | \leq 1. & (2) \end{matrix}

Mindez, átfordítva a feladat paramétereire, a következő feltételekhez vezet:

\begin{matrix} \frac{B^{2} l^{2}}{m L} \geq 2 \frac{g}{l}, \\ v_{0} \leq v_{0 max} = \frac{1}{B} \sqrt[]{\frac{3}{5} m L} (\frac{B^{2} l^{2}}{m L} - 2 \frac{g}{L}) . \end{matrix}

Ezek teljesülése esetén áll meg valahol a tekercs. A megállási szög koszinuszára kapjuk:

\begin{matrix} cos α_{{max}_{}^{}} = \frac{2 m g L}{B^{2} l^{3}} + \sqrt[]{{(1 - \frac{2 m g L}{B^{2} l^{3}})}^{2} - \frac{5 m L}{3 B^{2} l^{4}} v_{0}^{2}} . \end{matrix}

(A gyökjel előtt azért választottuk a pozitív előjelet, mert az felel meg nagyobb

cos α

-nak, tehát kisebb

α

szögnek. A tekercs nyilván ott áll meg, ahol először teljesül a megállás

ω = 0

feltétele.) A megoldásból látszik, hogy minél nagyobb a meglökés

v_{0}

sebessége, annál kisebb lesz

cos α_{{max}_{}^{}}

értéke, vagyis annál nagyobb

α_{{max}_{}^{}}

szögnél áll meg a tekercs, ahogy azt vártuk is.