Kezdőlap


Feladat:	2005. évi Eötvös fizikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Kitűző(k):	Gnädig Péter
Füzet:	2006/március, 171 - 174. oldal		PDF \| MathML
Témakör(ök):	Fényelhajlás (diffrakció)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2. Egy átlátszatlan lapon kicsiny lyukak vannak az 5. ábrán látható ,,háromszög-rács'' elrendezésben. A lapot monokromatikus, $λ$ hullámhosszúságú lézerfénnyel világítjuk meg merőlegesen. A rácsállandó $d = 100 λ$ .

5. ábra

Ábrázoljuk vázlatosan (a méretek, valamint a vízszintes és a függőleges irányok bejelölésével), hogy milyen elhajlási képet figyelhetünk meg a rácstól 3 m távolságra elhelyezett ernyőn!

Megoldás. Elevenítsük fel azokat az ismereteket, amelyek a síkbeli optikai rácson (párhuzamos, egymástól egyenlő távolságra lévő rések rendszerén) áthaladó monokromatikus fény diffrakciójára vonatkoznak! Világítsuk meg az optikai rácsot a síkjára merőleges, keskeny lézersugárral. A ráccsal párhuzamosan elhelyezett ernyőn ekkor közelítőleg egyenlő távolságra elhelyezkedő fényes foltokat látunk. Jelöljük

D

-vel a rácsállandót,

λ

-val a hullámhosszat. Az intenzitás menetét az elhajlási (diffrakciós) szög szinuszának függvényében a 6. ábra mutatja.

6. ábra

Az ábrán látható intenzitáseloszlást jól alátámasztja az a középiskolában tanult közelítés, amely szerint a rács rései olyan keskenyek, hogy egy-egy résen belül, az onnan kiinduló elemi hullámok azonos fázisban vannak (Huygens‐Fresnel-elv). Ugyanakkor két egymás melletti résből induló elemi hullámok erősítésének feltétele:

\begin{matrix} D sin α_{k} = k λ (k = 0, \pm 1, \pm 2, ...) . \end{matrix}

7. ábra

Ha az ernyő

S

távolságra van az optikai rácstól (7. ábra), akkor az első főmaximum távolsága a centrumtól

\begin{matrix} s_{1} \approx S \cdot sin α_{1} = S \frac{λ}{D}, \end{matrix}

és általában, a

k

-adik főmaximum távolsága

\begin{matrix} s_{k} \approx k S \frac{λ}{D} . \end{matrix}

(Itt kihasználtuk, hogy

λ ≪ d

miatt

α_{k} ≪ 1

, és így

sin α_{k} \approx α_{k}

.)
Térjünk rá a feladatban szereplő háromszögrácsra! Mivel a háromszögrács síkjára merőlegesen érkezik a fény, ezért minden egyes lyukból azonos fázisú elemi hullámok indulnak ki. Ezek a rácsra merőleges irányban tovább haladva biztosan erősítik egymást, útkülönbség nélkül,

α = 0

irányban jelölik ki a keletkező diffrakciós kép centrumát az elég távol lévő ernyőn.
Hol lesz ehhez a centrumhoz legközelebb újra egy erősítési hely az ernyőn? Milyen irányban?
Válasszuk ki valamelyik kicsiny lyukat. Gondolatban húzzunk ezen a lyukon át egy olyan egyenest, amelyik átmegy valamelyik, hozzá legközelebb eső lyukon. Ez az egyenes még egy sorozat lyukon fog áthaladni, amelyek mind

d

távolságra követik egymást. Most keressünk egy másik lyuksort, amelyen átmenő egyenes párhuzamos az előzővel. Sok ilyen lyuksort találunk, ezek egymástól

D = d \frac{\sqrt[]{3}}{2}

távolságra helyezkednek el (8. ábra). Figyeljük meg azt az irányt a térben, amely az elképzelt egyenesekre merőleges, de a már kijelölt centrum felé vezető iránnyal akkora

α_{1}

szöget zár be, hogy teljesül a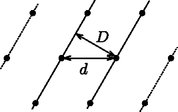

\begin{matrix} D sin α_{1} = λ \end{matrix}

összefüggés.

8. ábra

Ha az ilyen irányba haladó elemi hullámok eredőjét vizsgáljuk a messze lévő ernyőn, akkor azt látjuk, hogy a kiválasztott egyenesen elhelyezkedő lyukakból jövő elemi hullámok erősítik egymást, mert az ernyőhőz érve már szinte nincs is útkülönbség köztük. De a szomszédos egyenesen fekvő lyuksorból induló elemi hullámokkal is erősíteni fogják egymást, mert köztük az útkülönbség (

D sin α_{1}

) éppen

λ

-val egyenlő, és ugyanez igaz a többi egyenesen fekvő lyukakból induló hullámokra is. Tehát ebben az irányban az összes lyukon átjövő fény erősíteni fogja egymást!
Így az ernyőn a centrumhoz legközelebbi (egyik) erősítési helynek a centrumtól való távolsága:

\begin{matrix} s_{1} = S \frac{λ}{D} = \frac{2}{\sqrt[]{3}} S \frac{λ}{d} = 2 \sqrt[]{3} cm \approx 3, 4 cm . \end{matrix}

Hat ilyen pont lesz az ernyőn, amelyek egy ‐ a centrum körüli ‐ szabályos hatszög csúcsait jelölik ki. Ez azért van így, mert három, egymással 120‐

120^{\circ}

-os szöget bezáró egyenes-sereget (lyuksor-sereget) jelölhetünk ki a háromszögrácson.
Azt is észrevehetjük, hogy olyan helyen is lesz az ernyőn erősítés, melynek távolsága a centrumtól

2 s_{1},3 s_{1}, ...,

hiszen ekkor az egymás melletti lyuksorokból érkező hullámok

2 λ,3 λ, ...

útkülönbséggel találkoznak az ernyőn. Ezek szerint a rácson felvett mindegyik egyenes-sereg az ernyőn egy pontsorozatot eredményez. Ha a rácson elképzelt lyuksorok pl. vízszintes egyenesek mentén helyezkednek el, akkor az ernyőn keletkező pontsorozat egy függőleges egyenesre illeszkedik.
Hatágú ,,csillag'' lesz tehát a kép? Nem egészen, bár ezek a most elképzelt pontok mind megjelennek az ernyőn, de nem csak ezek jelennek meg! Képzeljük el például a háromszögrácson azt az egyenes- (lyuksor)-sereget, amelyet a 9. ábra bal oldalán látunk.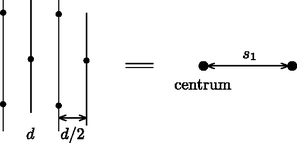

9. ábra

Ez egy

\frac{d}{2}

rácsállandójú optikai rácsnak felel meg, ezért az ernyőn a megfelelő erősítési helyek

\begin{matrix} s_{1}' = S \frac{λ}{\frac{d}{2}} = 6 cm \end{matrix}

távolságra követik egymást. Most is igaz, hogy minél sűrűbb optikai rácsba rendeződve képzeljük el a lyukakat, annál messzebb kerülnek egymástól a megfelelő erősítési helyek az ernyőn.
Meg lehet mutatni, hogy a háromszögrács ,,képe'' az ernyőn ugyancsak szabályos háromszögrács lesz, mert kölcsönösen egyértelműen egymáshoz rendelhető a lyukakra illeszthető egyenessereg és az ernyőn megjelenő, interferencia eredményezte ponthalmaz. (Ennek belátásához legközelebb Varjas Dániel jutott el, aki díjnyertes dolgozatában a különböző módon felvehető elemi cellák területének egyenlőségét használta ki.) Mégis lesz valami eltérés a lyukak alkotta háromszögrács és a diffrakciós pontok alkotta háromszögrács között (a pontok távolságában mutatkozó eltérésen kívül is): az egyik pontrács

90^{\circ}

-os elforgatottja a másiknak. (Most akár

30^{\circ}

-os elforgatottat is mondhatnánk, de egy téglalaprács esetén nagyon jól látszik, hogy

90^{\circ}

-os elforgatásról van szó.)
Mindezt a 10. ábra szemlélteti, melynek alsó részén a lyukak rácsa, felül pedig az ernyőn látható elhajlási kép látható, természetesen eltérő méretarányban.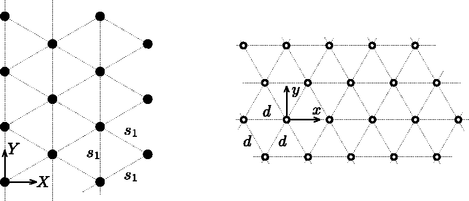

10. ábra

A feladatban szereplő háromszögrácsot úgy is előállíthatjuk, hogy három, egyenként

D

állandójú, közönséges optikai rácsot egymásra fektetünk. A feltétel csak annyi, hogy mindegyik rács rései a másik rács réseivel

60^{\circ}

-os szöget zárjanak be. Az így keletkező lyukak ugyan nem kör, hanem hatszög alakúak lesznek, de ha a rések szélessége sokkal kisebb a rácsállandónál, akkor ennek nincs jelentősége. Sőt! Ha elhagyjuk a harmadik rácsot, és csupán két, egymással

60^{\circ}

-os szöget bezáró rács diffrakciós képét vizsgáljuk, ez is ugyanaz lesz, mint az előbbiek. Ebben az esetben ugyanis a lyukak ugyan rombusz alakúak, de ugyanabban a szabályos háromszögrácsban rendeződnek el, tehát jó közelítésben ugyanazt a diffrakciós képet eredményezik. Az eredményhirdetéskor Komlósi István egyetemi hallgató mutatta be ezt a kísérletet.