Kezdőlap


Feladat:	2005. évi Eötvös fizikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Kitűző(k):	Károlyházy Frigyes
Füzet:	2006/március, 168 - 170. oldal		PDF \| MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Két rögzített, egymástól $l = 2 m$ távolságra levő csigán erős, de nem nyúlékony fonalat vezetünk át, és a végeire egy-egy $M = 1 kg$ tömegű testet erősítünk az 1. $(a)$ ábra szerint. (A fonal néhányszor 10 N terhelést bír ki szakadás nélkül. A csigák és a fonal tömege elhanyagolható.) Ha ujjunkkal lehúzzuk a fonal közepét úgy, hogy a két test $1$ ‐ $1$ méterrel megemelkedjék (1. $(b)$ ábra), majd elengedjük, a fonal elpattan, amikor $A$ és $B$ között ,,kiegyenesedik''. Ha azonban úgy engedjük el, hogy előbb egy ugyancsak 1 kg tömegű testet erősítünk a fonal közepéhez, akkor a fonal a továbbiakban nem szakad el.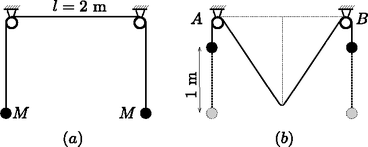

1. ábra

a)

Magyarázzuk meg a jelenséget!

b)

Mekkora erő feszíti a fonalat abban a pillanatban, amikor kiegyenesedik?

Megoldás.

a)

Azt kell észrevenni, hogy amikor a fonal kiegyenesedik, abban a pillanatban a fonalat két oldalról húzó testek már állnak. Rendkívül rövid idő alatt kell megállniuk, lefékeződniük arról a

v = \sqrt[]{2 g h} \approx 16

km/h sebességről, amire addigi mozgásuk (szabadesés) során felgyorsultak. (Itt és a továbbiakban

h = \frac{1}{2} l = 1 m

.) Ha a fékezést ,,pillanatszerűnek'' gondolnánk, vagyis a fékezés ideje

Δ t \to 0

lenne, akkor a testek gyorsulása és a fonalat feszítő

F

erő is minden határon túl nőne, ezért elpattanna a fonal.
A valóságban természetesen még a ,,nem nyúlékony'' fonal sem abszolút nyújthatatlan, hanem egy kicsit deformálható. Ehhez az alakváltozáshoz egy kicsiny, de véges

Δ t

idő szükséges, így a testek gyorsulása és ezzel együtt a fonalat feszítő erő ha nem is végtelenné, de nagyon naggyá válik. Mivel a fonal nem bír ki nagy erőt, elszakad.

b)

Ábrázoljuk a folyamat három jellemző állapotát! A 2.

(a)

ábrán a kezdőállapotot tüntettük fel, megjelölve közben a középső test egyensúlyi helyzetét is, amelyen maximális sebességgel átlendül. A 2.

(b)

ábrán a fonal középső része vízszintes, a középső test azonban még emelkedik fölfelé. A 2.

(c)

ábra azt a pillanatot mutatja, amikor a középső test éppen megáll. Ekkor ismét állnak a szélső testek is. (Persze elképzelhető, hogy a középső test fel se emelkedik a 2.

(b)

ábrán látható helyzetig, ezt a lehetőséget majd számítással kell ellenőriznünk.)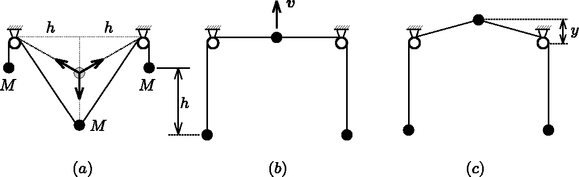

2. ábra

b)

kérdés megfogalmazása arra utal, hogy a fonal ki fog egyenesedni, tehát a középső test eljut a 2.

(b)

ábrán jelzett állapotba. Lesz-e ott sebessége? Ezt érdemes kiszámítanunk. Írjuk fel a munkatételt a 2.

(a)

helyzettől a 2.

(b)

-ig jelzett folyamatra! A szélső testek

h

utat süllyednek, a középső

h \sqrt[]{3}

utat emelkedik, ezért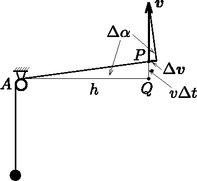

\begin{matrix} M g h - M g h \sqrt[]{3} + M g h = \frac{1}{2} M v^{2} . \end{matrix}

Felhasználtuk, hogy a 2.

(b)

helyzetben a szélső testek egy pillanatra megállnak, ezért csak a középső testnek lehet ekkor mozgási energiája. A felírt egyenletből a középső test sebessége:

v = \sqrt[]{2 g (2 - \sqrt[]{3}) h} > 0

. Tehát valóban emelkedik még a középső test. Meddig emelkedik? Ezt is kiszámíthatjuk, ha a 2.

(b)

és a 2.

(c)

állapotot hasonlítjuk össze energetikailag:

\begin{matrix} 2 M g (\sqrt[]{h^{2} + y^{2}} - h) + M g y = \frac{1}{2} M v^{2} . \end{matrix}

y

-ra nézve másodfokú egyenletté alakítható, melynek megoldásai:

y_{1} = - 1, 73 h

és

y_{2} = + 0, 22 h

. (Az első gyök nyilván a kezdőállapotot adja meg, a 2.

(c)

állapotnak

y_{2}

felel meg.)

3. ábra

Hogy válaszolni tudjunk a feladat

b)

kérdésére, vizsgáljuk meg tüzetesen a 2.

(b)

ábrán látható helyzetet! Ebben a pillanatban a fonalat feszítő erő gyorsítja az éppen álló, de felfelé induló szélső testeket. Mekkora ez a gyorsulás? Tegyük fel, hogy a bal oldali csigától a középső testhez vezető

A P

fonál

Δ t

idő alatt már egy kicsiny

Δ α

szöggel túllendült a vízszintes helyzeten (3. ábra). Jelöljük a szélső testek sebességét

Δ v

-vel! Ez a sebesség (a fonal nyújthatatlansága miatt) megegyezik a

P

pontban levő középső test sebességének

A P

irányú vetületével, vagyis

\begin{matrix} \frac{Δ v}{v} = sin Δ α \approx Δ α . \end{matrix}

Másrészt a

P Q A

derékszögű háromszögből

\begin{matrix} \frac{v Δ t}{h} = tg Δ α \approx Δ α . \end{matrix}

A fenti két egyenlet összevetéséből

\begin{matrix} Δ v = \frac{v^{2}}{h} Δ t, \end{matrix}

vagyis a szélső testek gyorsulására

\begin{matrix} a = \frac{Δ v}{Δ t} = \frac{v^{2}}{h} \end{matrix}

adódik.

Ugyanehhez a képlethez úgy is eljuthatunk, ha felírjuk, hogy a vízszinteshez közeli

A P

szakasz hossza időben hogyan változik. Mivel

P Q \approx v t

(ahol

t

a 2.

(b)

ábrán látható állapottól mért idő), Pitagorasz tétele szerint

\begin{matrix} A P = \sqrt[]{h^{2} + v^{2} t^{2}} = h \sqrt[]{1 + \frac{v^{2} t^{2}}{h^{2}}} \approx h + \frac{v^{2} t^{2}}{2 h} = h + \frac{a}{2} t^{2} . \end{matrix}

Ebből leolvashatjuk, hogy az

A P

szakasz hossza

a = v^{2} / h

gyorsulással növekszik, s a fonal nyújthatatlansága miatt a bal oldali test is ugyanekkora nagyságú, függőlegesen felfelé irányuló gyorsulással kell rendelkezzék.

A fonal által kifejtett erő a szélső testek mozgásegyenletéből kapható meg:

\begin{matrix} F_{fonal} - M g = M \frac{v^{2}}{h}, \end{matrix}

azaz

\begin{matrix} F_{fonal} = M g [1 + 2 (2 - \sqrt[]{3})] = 1, 536 M g \approx 15 N. \end{matrix}

Így már érthető, miért nem szakad el ebben a helyzetben a ,,néhányszor 10 N terhelést kibíró'' fonal.
Érdemes felfigyelni arra, hogy a szélső testek kétszer is emelkednek és kétszer is süllyednek egy-egy periódus során, hiszen a 2. ábrán feltüntetett mindhárom állapotban éppen állnak. Süllyedésük az idő függvényében nagyjából a 4. ábrán vázolt módon történik.

4. ábra