Feladat: 2003. évi Nemzetközi Fizika Diákolimpia 4. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 2003/december, 558 - 564. oldal  PDF  |  MathML 
Témakör(ök): Elektromos mérés, Fénytani (optikai) mérés, Modern fizikai mérés, Nemzetközi Fizika Diákolimpia
Hivatkozás(ok):Feladatok megoldásai: 2003/december: 2003. évi Nemzetközi Fizika Diákolimpia 4. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 34. Nemzetközi Fizikai Diákolimpia mérési feladata: Lézerdióda és nematikus folyadékkristály optikai tulajdonságai1
 

Vankó Péter
 

A mérés során a fényképen látható eszközök és anyagok álltak a versenyzők rendelkezésére:


A: fotodetektor, B: 2 darab polárszűrő forgatható foglalattal, C: 90∘-kal elcsavart nematikus (röviden 90∘ TN) folyadékkristály (röviden LC) cella forgatható LC foglalattal, D: jelgenerátor (részletes használati utasítással), E: lézerdióda (röviden LD), F: 2 darab multiméter (részletes használati utasítással), G: párhuzamos LC-cella, H: változtatható ellenállás, I: 2 darab telep, J: teleptartó, K: optikai sín; továbbá 2 darab áttetsző papír, vonalzó, fehér ragasztószalag (az eszközök megjelölésére), olló és 10 darab milliméterpapír.
 

A rész: A lézerdióda és a fotodetektor karakterisztikája
I. Bevezetés
A lézerdióda optikai tulajdonságai
 

A méréshez használt fényforrás egy 650 nm hullámhosszúságú félvezető lézer. Ha a lézerdióda (LD) árama nagyobb egy küszöbáramnál, a dióda monokromatikus, részlegesen polarizált, koherens fényt bocsát ki. Ha a lézerdióda árama kisebb egy küszöbértéknél, a kibocsátott fény intenzitása nagyon kicsi. A küszöbáram felett a fényerősség az áramerősség növekedésével rohamosan nő, és a két mennyiség között lineáris kapcsolat van. Ha az áram tovább nő, a fényerősség növekedési üteme a lézerdióda melegedése miatt csökken. Így a lézerdióda optimális működési tartománya az, ahol a fényerősség lineárisan függ az áramerősségtől. Az Ik küszöbáram definíció szerint az áramerősség tengely és a lineáris tartományra illesztett egyenes meghosszabbításának metszéspontja.
A méréshez használt fotodetektor egy fotodiódából és egy áramerősítőből áll. Ha a fotodiódára tápfeszültséget kapcsolunk, akkor a diódára eső fény hatására áram generálódik (fotoáram). Állandó hőmérsékleten, monokromatikus fény esetében a fotoáram egyenesen arányos a fényintenzitással. Az áramerősítő ezt a fotoáramot kimenő feszültségjellé alakítja. Ha a fényerősség nagyon nagy (a fotodióda tulajdonságai miatt) a kimenő feszültség 8 V tájékán telítődik (nem nő tovább). A fotodetektor csak a lineáris tartományban mutatja helyesen a fényintenzitást.
 

II. Mérési feladatok
 

Ahhoz, hogy a méréseket sikeresen el tudd végezni, nagyon fontos az elrendezés egyes részei közötti sugármenetek gondos beállítása. A fényforrásnak és a detektornak is megfelelően kell működnie. Az A rész ezekkel a kérdésekkel kapcsolatos.
 
 

1. ábra. Optikai összeállítás (LD: lézerdióda; PD: fotodetektor)
 

1. Szereld fel a lézerdiódát és a fotodetektort egy vízszintes egyenes mentén az optikai sínre, ahogy az 1. ábrán látható! Kapcsold össze a változtatható ellenállást, a telepet, az amper- és a voltmérőt, a lézerdiódát és a fotodetektort a 2. ábrának megfelelően! Állítsd be a változtatható ellenállást úgy, hogy a lézerdiódán átfolyó áram kb. 25 mA legyen, és a lézerdióda megfelelően világítson! Állítsd be a lézerdióda és a fotodetektor magasságát úgy, hogy a lézersugár a detektoron lévő kis lyukba juthasson és a fotodetektor maximális értéket mutasson!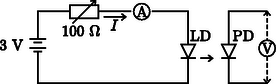
 
 

2. ábra. A lézerdióda és a fotodetektor elektromos kapcsolása
 

2. A fotodetektor kimenő feszültségét használd a lézerfény J intenzitásának leírására! Növeld a változtatható ellenállással a lézerdióda I áramát nullától a maximális értékig, és mérd meg J-t I függvényében! Győződj meg róla, hogy a mérés során megfelelő lépésekben növeled-e az áramot!
A.1 Mérd meg, foglald táblázatba és ábrázold J-t I függvényében (1,5 pont)!
A.2 Határozd meg a J‐I görbe lineáris tartományának maximális Imax áramát és annak mérési hibáját! Jelöld be a lineáris tartományt a J‐I görbén ,,nyilak'' segítségével, és határozd meg az Ik küszöbáramot és annak hibáját (3,5 pont)!
3. Válaszd a lézerdióda áramát Ik+2(Imax-Ik)/3 értékűre, és győződj meg róla, hogy a lézerdióda és a fotodetektor jól működik!
4. A következő (B) mérési részfeladat előkészítéséhez: Szereld fel az egyik polárszűrőt az optikai sínre a lézerdióda közelében a 3. ábrán látható módon! Győződj meg róla, hogy a lézersugár a polárszűrő középső részén halad át!
 
 

3. ábra. A polárszűrő (P) beállítása
 

Állítsd be a polárszűrőt úgy, hogy a beeső fénysugár merőleges legyen a polárszűrő síkjára! (Javaslat: Rakj be egy darab áttetsző papírt a fényútba, és ezen a ,,teszt-ernyőn'' ellenőrizd, hogy a beeső és a visszavert sugár egybeesik-e.)
5. Szerelj fel egy másik polárszűrőt is az optikai sínre az előzőhöz hasonlóan, és győződj meg róla, hogy minden helyesen van-e beállítva, azaz a fényforrás, a polárszűrők és a detektor egy egyenesbe esnek-e, és a polárszűrők merőlegesek-e a fénysugárra! Ne változtasd meg a lézerdióda áramát!
 

B rész: 90∘ TN LC-cella elektro-optikai kapcsolási karakterisztikája
I. Bevezetés
A nematikus folyadékkristály optikai tulajdonságai
 


1. Folyadékkristály
A folyadékkristály (LC = Liquid Christal) olyan állapota az anyagnak, ami a kristályos szilárd állapot és az amorf folyadék állapot között van. A nematikus LC-k szerves vegyületek, melyek hosszúkás, tűszerű molekulákból állnak. A molekulák irányítottsága (orientációja) elektromos erőtér segítségével szabályozható. Az LC eszközökhöz azonos vagy jól meghatározott orientációjú LC molekulákra van szükség. A méréshez használt LC-cella felépítése a 4. ábrán látható. Az üveg hordozólemezeket először egy vékony, elektromosan vezető, de optikailag átlátszó indium-ón-oxid (ITO = Indium-Tin-Oxid) réteggel vonják be, majd egy vékony polyimid (PI) ,,rendező'' réteget alakítanak ki. Ezután a PI réteg felszínét megcsiszolják, és ezzel mikroszkopikus árkokat alakítanak ki rajta. Ezek az árkok rendezik egy irányba az LC molekulákat, melyeket szendvicsszerűen két hordozó közé helyeznek. Ezzel a csiszolásos módszerrel a kívánt irányba orientált, jól rendezett LC-molekulák kerülnek a hordozók felszínére, és a molekulák közt ható erők hatására az egész LC-hasáb azonos irányítottságú lesz. Egy adott helyen a molekula-orientációt az LC adott helyen lévő direktorának nevezik.
 
 

4. ábra. A folyadékkristály (LC) cella szerkezete
 

Az LC-cellában megfigyelhető az ún. kettőstörés jelensége, amikor az anyagnak kétféle fő törésmutatója van. Ha a fény a direktor irányába terjed, akkor az összes polarizációs összetevő ugyanakkora vo=c/no sebességgel terjed, ahol no az ordinárius (rendes) törésmutató. Ezt a terjedési irányt (a direktor irányát) nevezik a cella optikai tengelyének. Ha a fény az optikai tengelyre merőleges irányba terjed, akkor két terjedési sebesség van. A fény elektromos mezejének az optikai tengelyre merőlegesen polarizált része vo=c/no sebességgel halad, míg az optikai tengellyel párhuzamosan polarizált rész ve=c/ne sebességgel halad, ahol ne az extraordinárius (rendellenes) törésmutató. Az optikai anizotrópia (pontosabban annak mértéke) az extraordinárius és az ordinárius törésmutató különbsége: Δn=ne-no.
 

2. 90∘-kal elcsavart nematikus LC-cella
A 90∘-kal elcsavart nematikus (TN = Twisted Nematic) cellában (5. ábra) a hátsó felület LC direktora 90∘-kal el van forgatva az első felülethez képest. Elöl a helyi direktor párhuzamos a polarizátor (első polárszűrő) polarizációs irányával. A belépő polarizálatlan fény az első polárszűrőben lineárisan polarizált fénnyé változik.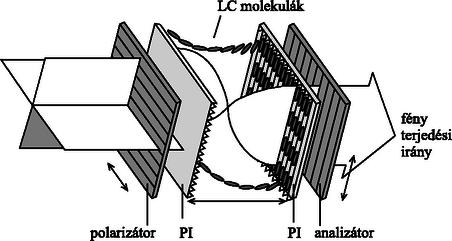
 
 

5. ábra. 90∘ TN LC-cella
 

Ha egy lineárisan polarizált fény halad át egy 90∘ TN cellán, akkor polarizációs iránya követi az LC direktorának csavarodását (a polarizált fény csak ne-t érzékeli), így a kilépő fénysugár is lineárisan polarizált marad, csak polarizációs iránya 90∘-kal elfordul. (Ezt ne által okozott polarizációs forgató hatásnak nevezzük, ehhez hasonlóan van no által okozott forgató hatás is.) Eszerint a 90∘ TN-cella normál fekete (NB = Normál Black) üzemmódjához az analizátor (a második polárszűrő) polarizációs irányát párhuzamosra kell állítani a polarizátor (az első polárszűrő) polarizációs irányával, mint ahogy a 6. ábrán látszik. Ha azonban az LC-cellára kapcsolt U feszültség értéke elér egy kritikus Uk értéket, az LC-molekulák igyekeznek beállni az alkalmazott külső elektromos tér irányába, ami itt megegyezik a fény terjedési irányával. Ennél fogva az LC-cella polarizációs irányt elforgató hatása folyamatosan csökken, és a fény átjuthat az analizátoron (a második polárszűrőn). A cella κ elektro-optikai kapcsolási meredekségét az U90-U10U10 képlet definiálja, ahol U10 és U90 azok a feszültségek, ahol a cellán áthaladó fény intenzitása eléri a maximális fényintenzitás 10%-át, illetve 90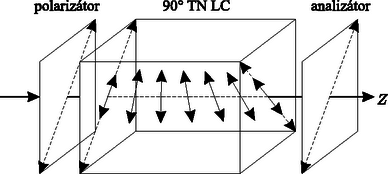%-át.
 
 

6. ábra. A 90∘ TN LC cella NB módusú működése
 

 
II. Mérési feladatok

1. Szereld fel az NB 90∘ TN LC-cellát a két polárszűrő közé! Állítsad a polárszűrők polarizációs irányát egymással párhuzamosra! Kapcsolj az üveghordozókat borító ITO kontaktusokra 100 Hz-es négyszögjelet a jelgenerátorból, és változtasd az alkalmazott U (effektív) feszültség nagyságát 0-tól 7,2 V-ig! (A fontos, érdekes pontoknál finoman, kis lépésekban változtasd a feszültséget!)
B.1 Mérd meg, foglald táblázatba és ábrázold az NB 90∘ TN LC-cella elektro-optikai kapcsolási görbéjét (vagyis J-t U függvényében), és határozd meg a κ=(U90-U10)/U10 kapcsolási meredekséget (5 pont)!
B.2 Határozd meg a NB 90∘ TN LC-cella kritikus Uk feszültségét! Mutasd meg egyértelműen, hogy a grafikonból hogyan határozod meg Uk értékét (2,5 pont)!
Figyelem! Amikor az alkalmazott külső feszültség eléri a kritikus feszültséget, a fényáteresztő képesség gyorsan és ,,törésmentesen'' nőni kezd!
 

C rész: Párhuzamosan rendezett LC-cella elektro-optikai kapcsolási karakterisztikája
I. Bevezetés
Homogén, párhuzamosan rendezett LC-cella optikai tulajdonságai
 

A párhuzamosan rendezett LC-cella esetében az elülső és a hátsó hordozón lévő direktorok párhuzamosak egymással (7. ábra). Ha egy polarizált fénysugár úgy esik a párhuzamosan rendezett cellára, hogy a polarizációs iránya párhuzamos az LC-cella direktorával (a csiszolt vájatok irányával), akkor semmi lényeges változás nem történik, mivel a fény tisztán extraordinárius sugárként viselkedik.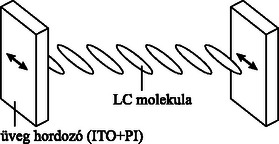
 
 

7. ábra. Homogén, párhuzamosan rendezett LC-cella
 

Ha viszont egy lineárisan polarizált fénysugár úgy esik (merőlegesen) a párhuzamosan rendezett cellára, hogy a polarizációs iránya θ=45∘-os szöget zár be a cella direktorának irányával (8. ábra), akkor fáziskülönbség (δ) lép fel az extraordinárius és az ordinárius sugarak különböző terjedési sebessége miatt. Ebben a θ=45∘-os elrendezésben, ha a két polárszűrő egymással párhuzamos, akkor a párhuzamosan rendezett LC-cella fényáteresztő képességét a következő összefüggés írja le:
T∥=cos2δ2.
A δ fáziskülönbség kifejezhető: δ=2πdΔn(U,λ)/λ, ahol d az LC-réteg vastagsága, λ a fény hullámhossza levegőben, U a váltakozó feszültség effektív értéke, és Δn, ami λ és U függvénye, az LC-cella optikai anizotrópiájának mértéke. Azt is meg kell jegyezni, hogy ha U=0, akkor Δn (=ne-no) maximális, és így δ-nak is ekkor van maximuma. Tehát Δn csökken, ha U növekszik.
Általános esetben:
T∥=1-sin22θsin2δ2,T⊥=sin22θsin2δ2,
ahol ∥ és ⊥ az analizátor és a polarizátor polarizációs irányának párhuzamos, illetve merőleges állására utal.
 
II. Mérési feladatok

1. Cseréld ki az NB 90∘ TN LC-cellát a párhuzamosan rendezett LC-cellával!
2. Állítsd be a θ=45∘-os konfigurációt és az U=0 értéket (8. ábra)! Legyen az analizátor és a polarizátor polarizációs iránya egymásra merőleges! Ezután forgasd a párhuzamosan rendezett LC-cellát addig, amíg az átmenő fény intenzitása el nem éri a maximális értékét (T⊥)! Ez a helyzet valósítja meg a θ=45∘ konfigurációt. Jegyezd fel T⊥ értékét! Ezután mérd meg ugyanebben az LC-cellában az áteresztőképességet abban az esetben is, ha az analizátor és a polarizátor polarizációs iránya párhuzamos (T∥)! (A mérés során most 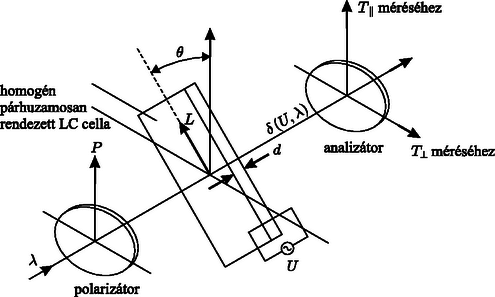U=0.)
 
 

8. ábra. A mérési elrendezés vázlata. (Az L nyíl a cella rendezési iránya)
 

C.1 Tudjuk, hogy a lézerfény hullámhossza 650 nm, az LC-réteg vastagsága 7,7 μm és hogy Δn=0,25. Felhasználva T⊥ és T∥ az előzőek szerint megmért értékét, számítsd ki a δ fáziskülönbség és a Δn optikai anizotrópia pontos értékét az adott LC-cellára U=0 esetében (2,5 pont)!
 
3. Az előzőekhez hasonlóan, továbbra is a θ=45∘-os konfigurációban mérjél! Kapcsolj 100 Hz-es négyszögjelet az ITO kontaktusokra, változtasd az U feszültség (effektív) értékét 0-tól 7 V-ig, és mérd ki az elektro-optikai kapcsolási görbét az analizátor és a polarizátor párhuzamos állásánál (T∥)!
 
(Megjegyzés: A T⊥ kapcsolási görbe kimérése hasznos lehet a T∥ mérés pontosságának fokozásához; azonban a T⊥ adatokra a következőkben nem lesz szükség.)
 
A függvény szélsőértékeinek közelében vedd fel sűrűbben a pontokat (különösen a 0,5‐4,0 V feszültségtartományban)!
 

C.2 Mérd meg, foglald táblázatba és ábrázold ennek a párhuzamosan rendezett LC-cellának a T∥ elektro-optikai kapcsolási görbéjét a θ=45∘-os konfigurációban (3 pont)!
C.3 Az elektro-optikai kapcsolási adatokból határozd meg azt az Uπ feszültséget, amelynél az LC-cellában a fázistolás π (azaz 180∘) (2 pont)!
 
Megjegyzések: 1. Ne felejtsd el, hogy Δn az U feszültség csökkenő függvénye!
2. Valószínűleg szükséged lesz interpolációra is Uπ pontos értékének meghatározásakor.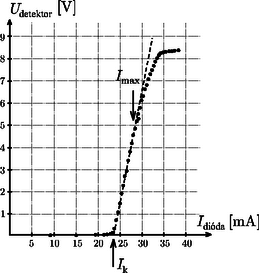
 

 
1A mérési feladat kidolgozására 5 óra állt rendelkezésre. A feladat szövegét ‐ amely eredetileg mintegy 13 oldal terjedelmű ‐ rövidítve, bizonyos technikai részletek (műszerkezelési útmutatások, balesetvédelmi tanácsok és a javítók munkáját megkönnyítő formai szabályok) elhagyásával közöljük.