Feladat:	1440. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1966/január, 29. oldal		PDF  |  MathML
Témakör(ök):	Vetítések, Féligszabályos testek, Sokszögek szerkesztése, Szabályos sokszögek geometriája, Szabályos sokszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok megoldásai: 1967/március: 1440. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.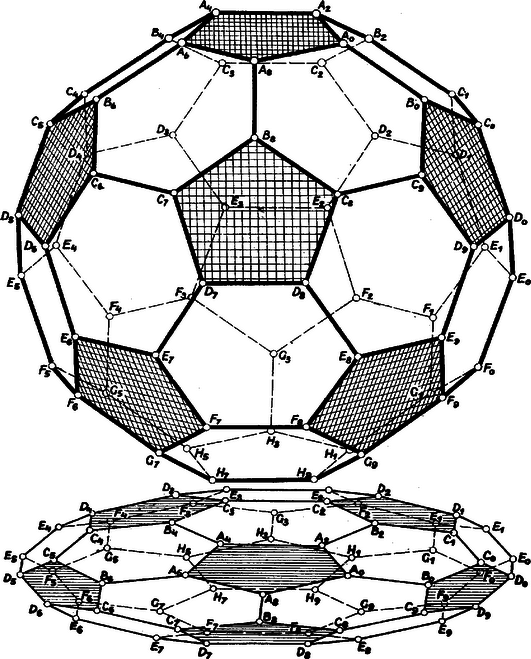     1. ábra   Sokan láttak már olyan futball‐labdát, melynek külsőjét 12 db szabályos ötszög alakú és 20 db szabályos hatszög alakú bőrdarabból varrták össze úgy, hogy mindegyik ötszögdarab csak hatszögdarabokhoz csatlakozik varrással, a hatszögdarabok egymás utáni oldalaihoz váltakozva ötszög- és hatszögdarabok csatlakoznak, és varrások összetalálkozásánál mindig 3 varrás fut össze. A bőrdarabokat síklapoknak tekintve a labda helyén egy sok szabályszerűséget mutató poliéder áll előttünk (1. ábra). Mutassuk meg a következőket:2 I. A poliéder mindegyik élével 5 további éle párhuzamos, mindegyik élre 12 más él merőleges. II. Ha a rajz síkján meg van rajzolva a poliéder egy ötszöglapja, ebből kiindulva a poliédernek ezen a lapsíkon levő vetületét megszerkeszthetjük egy szokásos háromszögvonalzó‐pár használatával. (A szimmetria alapján elég a vetület $2/5$ részét megszerkeszteni. Az ábra alján a poliédernek az egyik ötszöglapjával párhuzamos síkon levő vetülete látható távlati képben.) 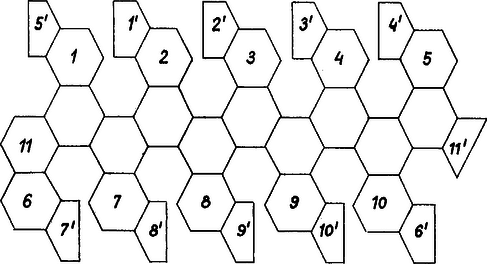    2. ábra   2A 2. ábra alapján olyan modell készíthető a poliéderről, melyen az ötszöglapok helyén lyuk van. Így is több érdekes tulajdonság fedezhető fel rajta.