Cím:	Mathematikai modellek II. Az inverzor.
Szerző(k):	Dr. Sós Ernő
Füzet:	1913/november, 62 - 64. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. II. Az inverzor.   A pantograf működését röviden úgy jellemezhetjük, hogy az adott $OA=r$ távolsághoz megadja annak $\lambda$-szorosát; az inverzor (invertere=megfordítani) ezzel szemben adott távolsághoz a vele reciprok $\frac{1}{r}$-t vagy általánosabban $\frac{\lambda }{r}$-t nyújtja. Itt is a szerkezet alapja a csuklókban mozgó paralelogramm ‐ és pedig jelen esetben rhombus ‐ melynek két szembenfekvő csúcsát két másik egyenlő szintén csuklóval összekötött rúd köti össze (1. ábra). 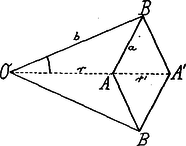    Ha $O$-t szilárdan tartom, úgy $A$-val együtt $A\text{'}$ is mozog, mégpedig ellenkező értelemben: ha $A$ közeledik $O$-hoz, $A\text{'}$ távolodik tőle és fordítva. Hogy $OA=r$ és $OA\text{'}=r\text{'}$ között az összefüggést megállapíthassuk, fejezzük ki $\text{cos}AOB$ értékét az $OAB$ és $OAB\text{'}$ háromszögekből. Ha jelölésünk $AB=a$, $OB=b$, úgy $\begin{array}{c}{\displaystyle \text{cos}AOB=\frac{r^2+b^2-a^2}{2br}=\frac{r{\text{'}}^2+b^2-a^2}{2br\text{'}}\mathrm{,}}\end{array}$ miből felszorzás útján $\begin{array}{c}{\displaystyle rr\text{'}\left(r-r\text{'}\right)+b^2\left(r\text{'}-r\right)-a^2\left(r\text{'}-r\right)=\left(r-r\text{'}\right)\left(rr\text{'}-b^2+a^2\right)=0.}\end{array}$ Ha tehát a számunkra lényegtelen $r-r\text{'}$ faktortól eltekintünk, mely csak egy elfajuló esetet jellemez, úgy az egyenletből $\begin{array}{c}{\displaystyle rr\text{'}=b^2-a^{2}r\text{'}=\frac{b^2-a^2}{r}\mathrm{,}}\end{array}$ $a$-t és $b$-t úgy választhatjuk, hogy $b^2-a^2=1$ (pl. $b=1\mathrm{,}\mathrm{25,}a=0\mathrm{,}75$), ekkor az átalakító képlet $r\text{'}=\frac{1}{r}$; az általános esetben $r\text{'}=\frac{\lambda }{r}$, hol $\lambda =b^2-a^2$. Az idom szimmetriájából következik, hogy $O\mathrm{,}A\mathrm{,}A\text{'}$ ugyanazon az egyenesen fekszenek, s így az $A$-nak $O$-ra vonatkozó poláris koordinátáiból $\left(r\mathrm{,}\phi \right)$ $A\text{'}$-éi ily alakban adódnak $\left(\frac{\lambda }{r}\mathrm{,}\phi \right)$. A műszer kivitelénél épp úgy, mint a pantografnál, $O$-ban szeg van, mely az egészet a rajzlaphoz rögzíti, $A$-ban vezető szeg, $A\text{'}$-ban ceruza van. Ha $A$ tetszésszerinti idomot ír le, úgy $A\text{'}$ egy másféle, hozzá nem hasonló idomot fog leírni, az ,,inverz'' idomot. Minthogy az $rr\text{'}=\lambda$ összefüggés kölcsönös $A$ és $A\text{'}$-ben a vezető szeg és a ceruza által leírt idomok ugyanazok, ha a kettő helyét a műszerben felcserélem. Ha $A\text{'}$ egyenest ír le, úgy $A$ kört, mely az $O$ ponton megy keresztül. 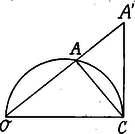    Ugyanis, ha az 2. ábrában $\text{cos}AOC$-t az $AOC\sim COA\text{'}$ háromszögekből kifejezzük: $\begin{array}{c}{\displaystyle \text{cos}AOC=\frac{OA}{OC}=\frac{OC}{OA\text{'}}\mathrm{,}\text{tehát}OA\cdot OA\text{'}={\overline{OC}}^2\mathrm{,}}\end{array}$ vagyis ugyanaz az összefüggés, mint $r$ és $r\text{'}$ között volt, ha ${\overline{OC}}^2$. Világos, hogy $A$-t az $OAC$ körön mozgatva, $A\text{'}$ a $CA\text{'}$ egyenes írja le. Ez a tulajdonsága adja meg gyakorlati fontosságát e műszernek, amennyiben segélyével az ,,egyenesvezetés'', vagyis körmozgásnak egyenes mozgássá való átalakítása elérhető anélkül, hogy súrlódó tagokat kellene közbeiktatni. Ecélból szerkesztette Peaucellier 1864-ben. Rendesen ugyan más mechanizmust, a Watt-féle parallelogrammot, szokás alkalmazni e célra, mert kevesebb tagból áll, de viszont a Watt csak közelítőleg ad egyenes vonalú mozgást, míg Peaucellier teljesen szigorúan egyenesben vezet. Azt, hogy $A$ az $O$ ponton átmenő körön mozogjon, úgy szokás elérni, hogy $A$ a szilárd $P$ ponttal van még összekötve és így körülötte $PA=PO$ sugarú kört írhat le. Az $A$ és $A\text{'}$ pontok kölcsönös megfelelése, az inverzió, a mértanban is rendkívül fontos. Ott az $OA\cdot OA\text{'}=\lambda$ összefüggést egyszerűbben olyképp értelmezik, hogy adott sugarú és $O$ középpontú körhöz $A\text{'}$-ból meghúzva az $A\text{'}T$ és $A\text{'}T\text{'}$ érintőket, $A$ mint a $TT\text{'}$ és $OA\text{'}$ egyenesek metszése adódik ki. 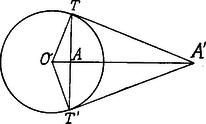    Fordítva a kör belsejében levő $A$ ponthoz a hozzá inverz $A\text{'}$ olyképp adódik, hogy az $OA$ átmérőre az $A$-ban reá merőleges $TT\text{'}$ húrt meghúzzuk, $A\text{'}$ az $OA$ meghosszabbításának és az $OT$-re merőleges $TA\text{'}$ egyenesnek metszőpontja. Az idomból rögtön látni, hogy $O\mathrm{,1}A\mathrm{,}A\text{'}$ ugyanazon egyenes pontjai, továbbá, minthogy $OTA$ derékszögű háromszög a középarányossági tétel alapján: $\begin{array}{c}{\displaystyle OA\cdot OA\text{'}={\overline{OT}}^2={\varrho }^2=\lambda \mathrm{.}}\end{array}$ A kör segítségével értelmezett inverzió, tehát teljesen azonos azzal, melyet a Peaucellier inverzióra nyújt. Az inverzió körének sugarát az utóbbinál akkor nyerjük, ha egy szélső helyzetben $A$ és $A\text{'}$ fedésbe jut, ekkor $BB\text{'}\perp OAA\text{'}$ és ekkor $\lambda =a^2-b^2={\varrho }^2$. Az inverzió műveletének egyik alapvető tulajdonsága, hogy köröket megint körökké alakít át. (Lásd 2. feladat.) Ezzel a kijelentéssel előbbi állításunk, hogy $O$-n átmenő kör egyenessé invertálódik, nem áll ellentmondásban, amennyiben az egyeneseket végtelen nagy sugarú köröknek tekinthetni. 1. feladat. Rudakból oly szerkezetek készítendők, melyek az $r8217;=r+\lambda$ és $r\text{'}=\lambda -r$, vagyis eltolásokat létesítenek. ($\lambda$ állandó.) 2. feladat. Bizonyítsuk be, hogy ha $A$ kört ír le, úgy $A\text{'}$ is kört fog leírni. 3. feladat. Megszerkeszthető-e a Peaucellier inverzor, ha $a>b$? s ha igen, hogyan jellemezhető az ilyen átalakítás.   Budapest. Dr. Sós Ernő.