Kezdőlap


Cím:	A XVI. Károly Irén fizikai tanulóverseny tételeinek megoldása
Szerző(k):	Auer György , Bak László , Reinhardt Ottó
Füzet:	1935/január, 118 - 121. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Vékony homogén rúd egyik végén átmenő vízszintes tengely körül foroghat, másik végétől számítva negyedében függőleges fonálra függesztjük; kérdés, hogy súlyának hányadrészével húzza a rúd a fonalat?

I. Megoldás. Az

A B

homogén rúd

A

végpontja körül foroghat; legyük fel, hogy az

A

ponton átmenő vízszintessel

α

szöget zár be.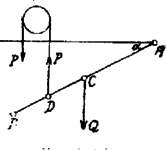

A B

rúd

C

felezőpontjában hat a súlya,

Q

. Ennek forgatónyomatéka az

A

pontra vonatkozólag, ha a rúd hossza

l, \frac{1}{2} Q l cos α

D

pontban, melyre nézve

B D = \frac{l}{4}

, tehát

A D = \frac{3 l}{4}

függőleges fonálra függesztve, valamely

P

erőt kell alkalmaznunk a fonál másik végén, hogy a rúd a jelzett helyzetben egyensúlyban legyen. Ezen

P

erő forgatónyomatéka:

\frac{3}{4} P l cos α

. Egyensúly esetén

\begin{matrix} \frac{1}{2} Q l cos α - \frac{3}{4} P l cos α = 0, azaz P = \frac{2 Q}{3} . \end{matrix}

Eszerint a rúd a fonalát súlyának

\frac{2}{3}

részével húzza.

Auer György (Baross Gábor r. VIII. o. Szeged).

II. Megoldás. A rúd

C

felezőpontjában ható

Q

súlyát két vele párhuzamos összetevőre bonthatjuk; ezek egyikének,

Q_{1}

-nek támadási pontja

A

, a másiké,

Q_{2}

-é

D

.
A párhuzamos összetevőkre vonatkozólag áll:

\begin{matrix} Q_{1} + Q_{2} = Q, & (1) \\ Q_{1} : Q_{2} = C D : C A = 1 : 2. & (2) \end{matrix}

(2)-ből

Q_{2} = 2 Q_{1}

. Helyettesítve ezt (1)-be

\begin{matrix} Q_{1} + 2 Q_{1} = 3 Q_{1} = Q, azaz Q_{1} = \frac{Q}{3} és Q_{2} = \frac{2 Q}{3} . \end{matrix}

D

pontban ható összetevő az egész rúd súlyának

\frac{2}{3}

része.

Ebben az esetben a rúd az

A

pontra súlyának

\frac{1}{3}

részével támaszkodik

2. Súlypontján átmenő forgástengellyel ellátott mágnestű percenként 24-et leng, ha forgástengelye függőleges. Hányat leng percenként, ha forgástengelye vízszintes és
a) párhuzamos a mágneses délvonallal,
b) merőleges a mágneses délvonalra.
Az észlelés helyén a mágneses lehajlás

60^{\circ}

Megoldás. A függőleges tengely körül lengő mágnestű lengési ideje

\begin{matrix} t = π \sqrt[]{\frac{K}{H M}} = \frac{60}{24} sec, \end{matrix}

ahol

K

a tű tehetetlenségi nyomatéka,

H

a földmágnesség intenzitásának horizontális komponense és

M

a tű mágneses nyomatéka.
a) A mágneses délvonallal párhuzamos tengely körül lengő tűre a föld mágnesség függőleges komponense,

V

hat; lengésideje tehát

\begin{matrix} t_{1} = π \sqrt[]{\frac{K}{V M}} = π \sqrt[]{\frac{K}{H tg i \cdot M}} = t \sqrt[]{\frac{1}{tg i}} = t \sqrt[]{cotg i}, \end{matrix}

ahol

i

a lehajlás szöge és

V = H tg i

.
b) A mágneses délvonalra merőleges tengely körül lengő tűre a teljes földmágnességi intenzitás,

I

hat, és

I = \frac{H}{cos i}

. A tű lengésideje

\begin{matrix} t_{2} = π \sqrt[]{\frac{K}{I M}} = π \sqrt[]{\frac{K cos i}{H M}} = t \sqrt[]{cos i} . \end{matrix}

Már most

\begin{matrix} t_{1} = \frac{60}{n_{1}} = \frac{60}{24} \sqrt[]{cotg i}, azaz n_{1} = 24 \sqrt[]{tg i} . \end{matrix}

n_{1}

jelenti a percenkénti lengések számát az

a)

esetben. Minthogy

\begin{matrix} tg i = tg 60^{\circ} = \sqrt[]{3}, n_{1} = 24 \sqrt[4]{3} = 31, 58. \end{matrix}

A b) esetben, percenként

n_{2}

lengésszámmal

\begin{matrix} t_{2} = \frac{60}{n_{2}} = \frac{60}{24} \sqrt[]{cos i}, és innen n_{2} = \frac{24}{\sqrt[]{cos i}} \\ cos i = cos 60^{\circ} \frac{1}{2} =, tehát n_{2} 4 \sqrt[]{2} = 33 \cdot 94. \end{matrix}

Reinhardt Ottó (Kegyesrandi g. VIII. o. Bp.).

Jegyzet. A különböző erők hatása alatt lengő ingáknak ‐ ugyanazon idő alatt végzett ‐ lengésszámai a ható erők négyzetgyökével arányosak; a mi esetünkben tehát

\begin{matrix} n : n_{1} : n_{2} = \sqrt[]{H} : \sqrt[]{V} : \sqrt[]{I} \\ n : n_{1} : n_{2} = \sqrt[]{H} : \sqrt[]{H tg i} : & \sqrt[]{\frac{H}{cos i}} \\ n : n_{1} : n_{2} = 1 : \sqrt[]{tg i} \cdot & \sqrt[]{\frac{1}{cos i}} \end{matrix}

n = 24

mellett

n_{1} = 24 \sqrt[]{tg} i

n_{2} = \frac{24}{\sqrt[]{cos i}}

3. Wheatstone-híd összeállításban a csúszó kontaktust úgy állítottuk be, hogy a galvanométer kitérést nem mutat. Bizonyítsuk be, hogyha az összeállításban az elemet a galvanométerrel felcseréljük, a galvanométer akkor sem fog kitérést mutatni.

Megoldás. Hogy a hídban a galvanométer ne mutasson kitérést, annak feltétele, hogy legyen:

\begin{matrix} r_{1} : r_{2} = ϱ_{1} : ϱ_{2}, \end{matrix}

(1)

ahol

ϱ_{1},

ϱ_{2}

A C

ill.

C D

ág,

r_{1}

ill.

r_{2}

A B

íll.

B D

ág ellenállását jelenti.

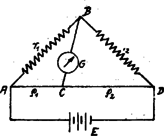Ha tehát az elemet

B

és

C

közé, a galvanométert

A

és

D

közé kapcsoljuk, akkor a

C A B

ág veszi át az előbbi

A B D

szerepét, a

C D B

ág pedig az

A C D

szerepét. Az

A D

hídban nem lesz áram, ha

\begin{matrix} r_{1} : ϱ_{1} = r_{2} : ϱ_{2} . \end{matrix}

(2)

(2) azonban megegyezik - a beltagok felcserélésével - az (1) feltétellel.

Bak László (Baksay Sándor ref. rg. VIII. o. Kunszentmiklós).