Cím:	Megoldásvázlatok a 2024/6. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Kozma Katalin Abigél, Győr
Füzet:	2024/október, 420 - 429. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg az $\text{log}{}_x\left(64x^2\right)=-4$ egyenletet a pozitív valós számok halmazán. (5 pont) $b)$ Oldjuk meg a ${\displaystyle \frac{\left(2x+14\right)\left(x-2\right)}{\left(x-7\right)\left(x+5\right)}}>2$ egyenlőtlenséget a valós számok halmazán. (7 pont)   Megoldás. $a)$ A logaritmus alapja $x$, ezért $x>0$ (ez a feladat kikötése is), és $x\ne 1$; $64x^2>0$ pedig nyilván teljesül. A logaritmus definícióját alkalmazzuk, majd rendezzük az egyenletet: $\begin{array}{c}{\displaystyle 64x^2=x^{-4}\iff 2^6=x^{-6}\iff {\left(\frac{1}{2}\right)}^{-6}=x^{-6}\iff x=\frac{1}{2}\mathrm{,}}\end{array}$ az ekvivalenciák $x\ne 0$, valamint a logaritmus-, illetve a hatványfüggvény egy-egyértelműsége miatt teljesülnek. Ellenőrzés: $\text{log}{}_{\frac{1}{2}}\left(64\cdot 0\mathrm{,}{5}^2\right)=\text{log}{}_{\frac{1}{2}}\left(64\cdot \frac{1}{4}\right)=\text{log}{}_{\frac{1}{2}}\left(16\right)=-4$, valóban. $b)$ A nevező kizárólag nemnulla tényezőket tartalmazhat, ezért $x\ne 7$, és $x\ne -5$. Nullára redukálunk, majd elvégezzük a kijelölt műveleteket: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{2x^2-4x+14x-28}{\left(x-7\right)\left(x+5\right)}-2>\mathrm{0,}}\hfill \\ \hfill {\displaystyle \frac{2x^2+10x-28-2\left(x-7\right)\left(x+5\right)}{\left(x-7\right)\left(x+5\right)}>\mathrm{0,}}\hfill \\ \hfill {\displaystyle \frac{14x+42}{\left(x-7\right)\left(x+5\right)}=\frac{14\left(x+3\right)}{\left(x-7\right)\left(x+5\right)}>0.}\hfill \end{array}}$ Látjuk, hogy a számláló $x=-3$-ban vált előjelet, a nevezőben pedig $x=7$-ben, illetve $x=-5$-ben történik előjelváltás. Ezek alapján elkészítjük a tényezők előjelét tartalmazó táblázatot: ${\displaystyle \begin{array}{|ccccc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mn>5</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>5</mn><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mn>3</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>3</mn><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo><mn>7</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>7</mn><mo stretchy="false"><</mo><mi>x</mi></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">+</mo><mn>5</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>14</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi><mo stretchy="false">+</mo><mn>3</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">-</mo><mn>7</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill \\ \hline\end{array}}$ A tört értéke pontosan akkor pozitív, ha páros számú negatív előjelű tényezőt tartalmaz. Jelen esetben a negatív tényezők száma $0$ vagy $2$, azaz mindhárom tényező pozitív (utolsó oszlop), vagy a nevező második tényezője pozitív, de a számláló és a nevező első tényezője negatív (második oszlop). 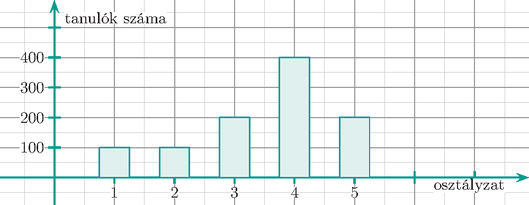Ekvivalens átalakításokat végeztünk és a megoldások megfelelnek a kikötésnek, így a megoldáshalmaz: $\begin{array}{c}{\displaystyle M=\left]-5;-3\right[\cup \left]7;\infty \right[\mathrm{.}}\end{array}$   2. Egy középiskola tanulói az elmúlt tanév végén matematikából az alábbi oszlopdiagramon szemléltetett osztályzatokat szerezték:     $a)$ Számítsuk ki az osztályzatok szórását. 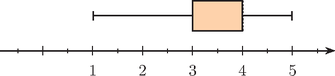(5 pont) $b)$ Készítsünk dobozdiagramot az adatok szemléltetésére. (7 pont)   Megoldás. $a)$ Az oszlopdiagramról leolvasott értékek alapján gyakoriságtáblázatot készítünk: ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{osztályzat}}\hfill & \hfill {\displaystyle \text{elégtelen}}\hfill & \hfill {\displaystyle \text{elégséges}}\hfill & \hfill {\displaystyle \text{közepes}}\hfill & \hfill {\displaystyle \text{jó}}\hfill & \hfill {\displaystyle \text{jeles}}\hfill \\ \hfill {\displaystyle \text{gyakoriság}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>100</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>100</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>200</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>400</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>200</mn></math>}}\hfill \\ \hline\end{array}}$ A szórás kiszámításához szükségünk van az átlagra: $\begin{array}{c}{\displaystyle \overline{X}=\frac{100\cdot 1+100\cdot 2+200\cdot 3+400\cdot 4+200\cdot 5}{100+100+200+400+200}=\frac{3500}{1000}=3\mathrm{,}5.}\end{array}$ Ennek segítségével meghatározzuk a szórást: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \sigma =\sqrt[]{\frac{100\cdot {\left(-2\mathrm{,}5\right)}^2+100\cdot {\left(-1\mathrm{,}5\right)}^2+200\cdot {\left(-0\mathrm{,}5\right)}^2+400\cdot 0\mathrm{,}{5}^2+200\cdot 1\mathrm{,}{5}^2}{1000}}=}\hfill \\ \hfill {\displaystyle =\sqrt[]{1\mathrm{,}45}\approx 1\mathrm{,}204.}\hfill \end{array}}$ $b)$ A dobozdiagram elkészítéséhez meghatározzuk az alsó kvartilist, a mediánt és a felső kvartilist. Az adatok növekvő sorrendben szerepelnek a gyakoriság táblázatban. A két középső az $500$. és az $501$. elem, mindkettő $4$, így ezek átlaga is, azaz a medián is $4$. Hasonlóképpen kapjuk, hogy az alsó kvartilis $3$, a felső kvartilis pedig $4$, azaz egyenlő a mediánnal, így a mediánt a doboz jobb szélén jelöljük be (lásd az ábrán).       3. $a)$ Három pozitív egész szám szorzata $33339600$. Az elsőt $3$-mal, a másodikat $4$-gyel, a harmadikat $5$-tel megszorozva ugyanazt a számot kapjuk. Melyek ezek a számok? 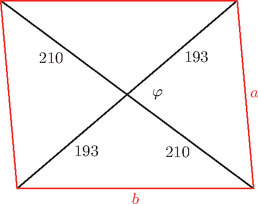(5 pont) $b)$ Egy paralelogramma átlói által közbezárt szög nagysága ${77}^{\circ }17\text{'}$, az átlók hossza $386\text{cm}$ és $42\text{dm}$. Adjuk meg (egészre kerekítve) a paralelogramma oldalainak centiméterben mért hosszát. (7 pont)   Megoldás. $a)$ Az első számot $a$-val, a másodikat $b$-vel, a harmadikat $c$-vel jelöljük. A feltételek alapján $abc=33339600$, és $3a=4b=5c=x$. Ekkor $a=\frac{x}{3}$, $b=\frac{x}{4}$, $c=\frac{x}{5}$. A három szám szorzata: $\begin{array}{c}{\displaystyle \frac{x}{3}\cdot \frac{x}{4}\cdot \frac{x}{5}=33339\mathrm{600,}}\end{array}$ amiből $x^3=60\cdot 33339600$, ezért $x=\sqrt[3]{60\cdot 33339600}=1260$. A keresett három szám, rendre: $a={\displaystyle \frac{1260}{3}}=420$, $b={\displaystyle \frac{1260}{4}}=315$ és $c={\displaystyle \frac{1260}{5}}=252$. Ezek valóban kielégítik a feladat feltételeit. $b)$ Bármely paralelogramma középpontosan szimmetrikus az átlók metszéspontjára, ezért az átlók két-két egybevágó háromszögre bontják a paralelogrammát. Jelen esetben e háromszögek egyik oldala $\frac{386}{2}=193$ cm, másik oldala pedig $\frac{42}{2}=21\text{dm}=210$ cm hosszúságú (lásd a mellékelt ábrán).     Az átlók által bezárt szög ($\phi ={77}^{\circ }17\text{'}$) ismeretében alkalmazhatjuk a koszinusztételt, ezzel megkapjuk a paralelogramma rövidebbik oldalának hosszát: $\begin{array}{c}{\displaystyle a^2={193}^2+{210}^2-2\cdot 193\cdot 210\cdot \text{cos}\left({77}^{\circ }17\text{'}\right)\approx 63505\mathrm{,}\mathrm{26,}}\end{array}$ amiből $a\approx 252$ cm. A paralelogramma hosszabbik oldalát hasonlóképpen kapjuk, ám ebben a háromszögben a $193$ és $210$ cm hosszúságú oldalak ${180}^{\circ }-{77}^{\circ }17\text{'}={102}^{\circ }43\text{'}$ nagyságú szöget zárnak be. A koszinusztételt használjuk ismét: $\begin{array}{c}{\displaystyle b^2={193}^2+{210}^2-2\cdot 193\cdot 210\cdot \text{cos}\left({102}^{\circ }43\text{'}\right)\approx 99192\mathrm{,}\mathrm{74,}}\end{array}$ amiből $b\approx 315$ cm. A paralelogramma oldalainak hossza egész centiméterekre kerekítve $252$ és $315$ cm.   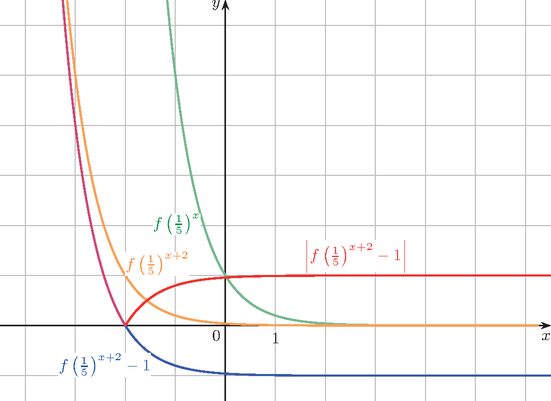4. $a)$ Ábrázoljuk az $f:\left]-3;3\right[\to \text{R}$; $f\left(x\right)=\left|{\left({\displaystyle \frac{1}{5}}\right)}^{x+2}-1\right|$ függvény grafikonját koordináta-rendszerben, és adjuk meg $f$ értékkészletét. (6 pont) $b)$ Határozzuk meg az $f$ értelmezési tartományának azon elemeit, amelyekre $f\left(x\right)=0\mathrm{,}8$. (6 pont) $c)$ Hol metszi az $f$ függvény grafikonja az $y$-tengelyt? (3 pont)   Megoldás. $a)$ Függvénytranszformációk segítségével ‐ az alábbi ábrán látható ‐ négy lépésben ábrázoljuk a grafikont.     A függvény értékkészlete: $R=\left[0;4\right[$. $b)$ Megoldjuk az $\left|{\left(\frac{1}{5}\right)}^{x+2}-1\right|=0\mathrm{,}8$ egyenletet. 1. eset ${\left(\frac{1}{5}\right)}^{x+2}-1=0\mathrm{,}8$, amiből ${\left(\frac{1}{5}\right)}^{x+2}=1\mathrm{,}8$, innen $x_1=\text{log}{}_{\frac{1}{5}}1\mathrm{,}8-2\approx -2\mathrm{,}365$. 2. eset ${\left(\frac{1}{5}\right)}^{x+2}-1=-0\mathrm{,}8$, amiből ${\left(\frac{1}{5}\right)}^{x+2}=\frac{1}{5}$, innen $x_2=-1$. Mindkét szám eleme az értelmezési tartománynak, így az $f$ függvény a $0\mathrm{,}8$ értéket két helyen, az $x_1=\text{log}{}_{\frac{1}{5}}1\mathrm{,}8-2$-ben és az $x_2=-1$-ben veszi fel. $c)$ Az $y$ tengelyen $x=0$, tehát kiszámítjuk $f\left(0\right)$-t. $\begin{array}{c}{\displaystyle f\left(0\right)=\left|{\left(\frac{1}{5}\right)}^{0+2}-1\right|=\left|\frac{1}{25}-1\right|=\left|-\frac{24}{25}\right|=\frac{24}{25}\mathrm{.}}\end{array}$ A grafikon az $y$ tengelyt az $M\left(0;\frac{24}{25}\right)$ pontban metszi.   II. rész   5. Egy derékszögű háromszög oldalhosszai számtani sorozatot alkotnak (azaz a hosszabb befogó ugyanannyival nagyobb a rövidebb befogónál, amennyivel az átfogó hosszabb nála). $a)$ Hányszorosa a háromszög köré írt kör területe a háromszögbe írható kör területének? (8 pont) $b)$ A háromszög átfogójához tartozó magasságának hossza $24$ egység. Mekkora a háromszög kerülete? (4 pont) $c)$ Adott az $a_n={\displaystyle \frac{42n^3-24n+2000}{6n^2-100}}$ sorozat. Konvergens-e ez a sorozat? Indokoljuk válaszunkat. 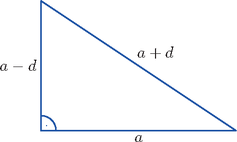(4 pont)   Megoldás. $a)$ Ábrát készítünk, amelyen a hosszabbik befogót $a$-val, a differenciát $d$-vel jelöljük ($0<d<a$ a geometriai tartalom miatt). Ekkor a rövidebb befogó hossza $a-d$, az átfogóé pedig $a+d$.     Pitagorasz tételét alkalmazzuk, hiszen derékszögű a háromszög. ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(a-d\right)}^2+a^2={\left(a+d\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle a^2-2ad+d^2+a^2=a^2+2ad+d^2\mathrm{.}}\hfill \end{array}}$ Rendezés után kiemelünk $a$-t: $\begin{array}{c}{\displaystyle a^2-4ad=a\left(a-4d\right)=\mathrm{0,}}\end{array}$ ami azt jelenti, hogy $a=0$, vagy $a-4d=0$.   Mivel $a>d>0$, ezért csak a második megoldás megfelelő, azaz $a=4d$, ekkor a háromszög oldalhosszai növekvő sorrendben: $3d$; $4d$; $5d$. Ismert, hogy a derékszögű háromszög köré írható körének sugara az átfogó felével egyenlő, azaz $R=2\mathrm{,}5d$. A beírt kör sugarát többféleképpen, például akár területképletek segítségével is meghatározhatjuk. Egyrészt a háromszög területe a befogóhosszak szorzatának a fele: $\begin{array}{c}{\displaystyle T_{▵}=\frac{3d\cdot 4d}{2}=6d^2\mathrm{,}}\end{array}$ másrészt $T_{▵}=r\cdot s$, ahol $r$ a beírt kör sugara, $s$ pedig a háromszög kerületének felével egyenlő, azaz $\begin{array}{c}{\displaystyle s=\frac{K_{▵}}{2}=\frac{3d+4d+5d}{2}=6d\mathrm{.}}\end{array}$ Kifejezzük $r$-et: $\begin{array}{c}{\displaystyle r=\frac{T_{▵}}{s}=\frac{6d^2}{6d}=d\mathrm{.}}\end{array}$ Vagy másképp, a csúcsokból a beírt körhöz húzott érintőszakaszok hosszából: $5d=\left(3d-r\right)+\left(4d-r\right)=7d-2r$, tehát $r=d$. A háromszög köréírt, illetve beírt körének területaránya: $\begin{array}{c}{\displaystyle \frac{R^2\pi }{r^2\pi }=\frac{{\left(2\mathrm{,}5d\right)}^2}{d^2}=6\mathrm{,}25.}\end{array}$ $b)$ Felhasználjuk, hogy $T_{▵}=6d^2$, és egy újabb területképletet alkalmazunk: $\begin{array}{c}{\displaystyle T_{▵}=\frac{c\cdot m_c}{2}\mathrm{,}}\end{array}$ ahol $c$ az átfogó hossza, azaz esetünkben $5d$, $m_c$ pedig az átfogóhoz tartozó magasság hossza, azaz $24$ egység. Mindezek alapján felírjuk a $\begin{array}{c}{\displaystyle 6d^2=\frac{5d\cdot 24}{2}}\end{array}$ egyenletet, amiből $d=\frac{5\cdot 24}{6\cdot 2}=10$. A háromszög kerülete $\begin{array}{c}{\displaystyle K_{▵}=3d+4d+5d=12d=12\cdot 10=120\text{(egység)}\mathrm{.}}\end{array}$ $c)$ Először osszuk a számlálót és a nevezőt is (a pozitív) $n^2$-tel. Ezután alkalmazzuk a sorozatok határértékére vonatkozó tételeket, illetve néhány ismert határértéket az alábbiak szerint: $\begin{array}{c}{\displaystyle \underset{n\to \infty }{\overset{}{\text{lim}}}\frac{42n^3-24n+2000}{6n^2-100}=\underset{n\to \infty }{\overset{}{\text{lim}}}\frac{42n-\frac{24}{n}+\frac{2000}{n^2}}{6-\frac{100}{n^2}}=\frac{\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}42n-\frac{24}{n}+\frac{2000}{n^2}}{\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}6-\frac{100}{n^2}}\mathrm{.}}\end{array}$ Itt $\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}42n-\frac{24}{n}+\frac{2000}{n^2}=\infty$, $\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}6-\frac{100}{n^2}=6$, azaz a sorozat végtelenhez tart, tehát divergens (nem konvergens).   6. Legyen $T$ azon $12$-jegyű pozitív egész számok halmaza, amelyek tízes számrendszerbeli alakjában legalább egyszer szerepel a $2024$ blokk. ($T$ eleme például a $120245678900$ és a $202477772024$, viszont nem eleme az $520022444202$.) $a)$ Hány elemű a $T$ halmaz? (8 pont) $b)$ Pistike a $T$ halmazból véletlenszerűen kiválaszt egyszerre három számot. Mekkora a valószínűsége, hogy mindhárom szám $1$-nél többször tartalmazza a $2024$ blokkot? (5 pont) $c)$ Móricka a $T$ halmazból véletlenszerűen visszatevéssel választ ki három számot. Mekkora a valószínűsége, hogy mindhárom szám $1$-nél többször tartalmazza a $2024$ blokkot? (3 pont)   Megoldás. $a)$ A 2024-es blokkok száma alapján végezzük az összeszámlálást. Ha van egy 2024-es blokk, akkor az lehet a szám legelején, ekkor a maradék 8 helyre bármilyen számjegy kerülhet, így ${10}^8$ darab ilyen szám van. Ha az adott blokk nem legelöl van, akkor 8-féleképpen rakhatjuk le, az első számjegy nem lehet nulla, így 9-féle értéket kaphat, a többi 7 helyre 0-tól 9-ig bármi. Ez összesen $8\cdot 9\cdot {10}^7=7\mathrm{,}2\cdot {10}^8$ darab szám. Az imént a pontosan két 2024-es blokkot tartalmazókat kétszer, a pontosan három ilyen blokkot tartalmazókat háromszor számoltuk. Ezért egyszer levonjuk a pontosan két ilyen blokkot tartalmazók számát, amihez most meghatározzuk ezek számát. Ha az egyik 2024-es blokk legelöl van, akkor a másik ilyen blokkot 5-féleképpen helyezhetjük el (vagy közvetlenül a másik után, vagy 1, 2, 3, illetve 4 helyet kihagyva ‐ több helyet nem hagyhatunk ki, mert akkor legalább 13-jegyű számot kapnánk). A maradék 4 helyre bármilyen számjegy kerülhet, így $5\cdot {10}^4=50000$ darab ilyen szám van. Ha pedig nem a 2024 van a szám legelején, akkor az első számjegy 9-féle lehet, utána a két adott blokkot a maradék 5 helyre (az első 2024 a balról 11., 10., 9., 8. helyi értékeken kezdődhet, a második ezekhez rendre 4, 3, 2, 1-féleképpen helyezhető el) 10-féleképpen helyezhetjük el, majd a még üresen maradt három helyet tetszőlegesen kitölthetjük, tehát ilyen számból $9\cdot 10\cdot {10}^3=90000$ darab van. Végül 3 darab 4-jegyű blokkot csupán 1-féleképpen, sorban egymás mellé helyezhetünk el, így egyetlen szám van, amely pontosan 3 blokkot tartalmaz. Ebben a lépésben a pontosan két 2024-es blokkot tartalmazó számokat egyszer számoltuk meg (így tényleg egyszer kell levonni), a három blokkot tartalmazókat pedig $\left(\genfrac{}{}{0ex}{}{3}{2}\right)=3$-szor. Ezért hozzá kell adni egyszer a pontosan 3 blokkot tartalmazókat, így (a logikai szita formula alapján is) összesen $\begin{array}{c}{\displaystyle {10}^8+7\mathrm{,}2\cdot {10}^8-50000-90000+1=820000000-140000+1=819860001}\end{array}$ ilyen 12-jegyű szám van, ami éppen a $T$ halmaz elemszámát adja. $b)$ Az $a)$ feladatrészben láttuk, hogy olyan 12-jegyű számból, amely legalább két 2024-es blokkot tartalmaz nem lehet több, mint $5\cdot {10}^4+9\cdot {10}^4=140000$ darab. Valójában ennél 2-vel kevesebb, azaz $139998$ darab van, hiszen a $202420242024$ számot háromszor is megszámoltuk, más számot pedig nem számoltunk meg többször. Pistike tehát $819860001$ szám közül választ hármat, azaz összesen $\left(\genfrac{}{}{0ex}{}{819860001}{3}\right)$ eset van. A kedvező esetek száma $\left(\genfrac{}{}{0ex}{}{139998}{3}\right)$, így a kérdezett valószínűség $\begin{array}{c}{\displaystyle p=\frac{\left(\genfrac{}{}{0ex}{}{139998}{3}\right)}{\left(\genfrac{}{}{0ex}{}{819860001}{3}\right)}\left(\approx 4\mathrm{,}97894\cdot {10}^{-12}\right)\mathrm{.}}\end{array}$ $c)$ Móricka visszatevéssel választ háromszor, így a valószínűség $\begin{array}{c}{\displaystyle p={\left(\frac{139998}{819860001}\right)}^3\left(\approx 4\mathrm{,}97905\cdot {10}^{-12}\right)\mathrm{.}}\end{array}$   7. $a)$ Határozzuk meg az alábbi állítások logikai értékét. Indokoljuk válaszunkat. (8 pont) A: Van olyan függvény, amelyet négyszer egymás után deriválva önmagát kapjuk. B: Ha egy függvény folytonos egy pontban, akkor abban a pontban differenciálható. C: Ha egy függvénynek egy pontban az első és a második deriváltja is nulla, akkor abban a pontban inflexiós pontja van. $b)$ Fogalmazzuk meg az előző feladatrész B állításának megfordítását és állapítsuk meg a megfordítás logikai értékét. (Indoklás nem szükséges.) (3 pont) $c)$ Fogalmazzuk meg a $b)$ feladatrész megoldásaként leírt állítás tagadását. (2 pont) $d)$ Fogalmazzuk meg az $a)$ feladatrész C állításának megfordítását és állapítsuk meg a megfordítás logikai értékét. (Indoklás nem szükséges.) (3 pont)   Megoldás. $a)$ A: Igaz, például $e^x$, $\text{sin}x$, $\text{cos}x$. konstans 0. (Egy helyes példa elegendő.) B: Hamis, például $\left|x\right|$ a $0$-ban. C: Hamis, például $x^4$ a $0$-ban. $b)$ Ha egy függvény differenciálható egy pontban, akkor abban a pontban folytonos. Logikai értéke: Igaz. $c)$ Az $b)$-ben megfogalmazott állítás tagadása: ,,Van olyan függvény, amely differenciálható egy pontban, de ott nem folytonos.'' (Természetesen hamis.) $d)$ Ha egy függvénynek inflexiós pontja van egy pontban, akkor abban a pontban az első és a második derivált is nulla. Logikai értéke: Hamis. (Például a $\text{sin}x$ függvénynek a 0-ban inflexiós pontja van, de a deriváltja ebben a pontban nem 0.)   8. Adott a $k_1:x^2+y^2-20x+10y-19=0$ egyenletű kör. A $k_2$ kör kerülete a $k_1$ kör kerületénél ennek $75\%$-ával kisebb. A két kör koncentrikus. $a)$ Írjuk fel a $k_2$ kör egyenletét. (5 pont) $b)$ Mutassuk meg, hogy a $P\left(10;-2\right)$ pont illeszkedik a $k_1$ vagy a $k_2$ körre. (3 pont) $c)$ Határozzuk meg a $k_2$ kör $Q\left(7;-5\right)$ pontjában húzott érintőegyenesének egyenletét. (5 pont) A $k_1$ kör belsejében véletlenszerűen kiválasztunk egy pontot. $d)$ Mekkora a valószínűsége, hogy a kiválasztott pont a $k_2$ körön kívül van, ha a körön bármely alakzat eltalálásának valószínűsége egyenesen arányos annak területével? (3 pont)   Megoldás. $a)$ A $k_1$ kör egyenletét átalakítjuk: $\begin{array}{c}{\displaystyle {\left(x-10\right)}^2+{\left(y+5\right)}^2=\mathrm{144,}}\end{array}$ ebből látjuk, hogy a középpont $O_1\left(10;-5\right)$, a sugár pedig $r_1=\sqrt[]{144}=12$. A körök koncentrikusak, ezért $O_1=O_2$, és $k_2$ kerülete $75\%$-kal kisebb, mint $k_1$-é, ezért a sugarakra is ugyanez fennáll, azaz $r_2=\mathrm{0,}25\cdot r_1=\mathrm{0,}25\cdot 12=3.$ Így a kisebb, $k_2$ kör egyenlete: $\begin{array}{c}{\displaystyle k_2:{\left(x-10\right)}^2+{\left(y+5\right)}^2=9.}\end{array}$ $b)$ A $P$ koordinátáit behelyettesítve azt kapjuk, hogy $\begin{array}{c}{\displaystyle {\left(10-10\right)}^2+{\left(-2+5\right)}^2=0^2+3^2=\mathrm{9,}}\end{array}$ ahonnan $P\in k_2$, azaz igazoltuk, hogy a $P$ pont illeszkedik a $k_2$ körre. $c)$ A $Q\left(7;-5\right)$ pont koordintái kielégítik a $k_2$ kör egyenletét, így $Q$ valóban rajta van ezen a körön. A kör érintője merőleges az érintési pontba húzott sugárra, ezért a sugárvektor normálvektora az érintőegyenesnek: $\begin{array}{c}{\displaystyle {\text{n}}_e=\overrightarrow{Q{O}_2}=\left(10-7;-5-\left(-5\right)\right)=\left(3;0\right)\mathrm{.}}\end{array}$ Az érintő átmegy a $Q$ ponton, így a normálvektoros egyenlet felírásához megvan minden szükséges adatunk: $\begin{array}{c}{\displaystyle e:3\cdot x+0\cdot y=3\cdot 7+0\cdot \left(-5\right)\mathrm{,}}\end{array}$ ahonnan $x=7$. Az érintőegyenes egyenlete: $e:x=7$. 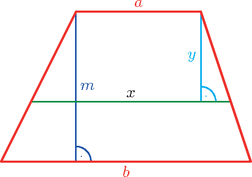$d)$ A geometriai valószínűségi modell alapján a keresett valószínűséget a megfelelő területek aránya adja: $\begin{array}{c}{\displaystyle p=\frac{T_1-T_2}{T_1}=\frac{{12}^2\cdot \pi -3^2\cdot \pi }{{12}^2\cdot \pi }=\frac{144-9}{144}=\frac{15}{16}\mathrm{.}}\end{array}$   9. $a)$ Bizonyítsuk be, hogy bármely trapéz területét felező, az alapokkal párhuzamos szakasz hossza éppen az alapok négyzetes közepével egyenlő. (11 pont) $b)$ Egy trapéz egyik alapjának hossza $5\text{cm}$, a trapéz területét felező, az alapokkal párhuzamos szakasz hossza $45\text{cm}$. Számítsuk ki a másik alap hosszának pontos értékét. (5 pont)   Megoldás. $a)$ Készítsünk ábrát, és használjuk a jelöléseit.     A feladat szövegéből következik, hogy az $x$ hosszúságú szakasz két kisebb trapézra bontja az eredeti trapézt, a területét pedig felezi. Ebből az következik, hogy a nagy trapéz területe kétszerese a kisebb trapézok területének, így felírjuk a következő egyenletrendszert: $\begin{array}{c}{\displaystyle \frac{a+b}{2}m=2\cdot \frac{a+x}{2}y=\left(a+x\right)y\mathrm{,}}\end{array}$ (1) $\begin{array}{c}{\displaystyle \frac{a+b}{2}m=2\cdot \frac{b+x}{2}\left(m-y\right)=\left(b+x\right)\left(m-y\right)\mathrm{.}}\end{array}$ (2) Kifejezzük $y$-t az (1)-ből: $y=\frac{\left(a+b\right)m}{2\left(a+x\right)}$ (a geometriai jelentésükből adódóan $a$ és $x$ is pozitív), majd behelyettesítjük (2)-be: $\begin{array}{c}{\displaystyle \left(a+b\right)m=2\left(b+x\right)m\left(1-\frac{a+b}{2\left(a+x\right)}\right)\mathrm{.}}\end{array}$ Látjuk, hogy mindkét oldalon szorzótényező a (pozitív) $m$, ezért mindkét oldalt elosztjuk vele, majd rendezzük az egyenletet: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \left(a+b\right)\left(a+x\right)=\left(b+x\right)\left(2x+2x-\left(a+b\right)\right)=\left(b+x\right)\left(a-b+2x\right)}\hfill \\ \hfill {\displaystyle a^2+ab+ax+bx=ab-b^2+2bx+ax-bx+2x^2}\hfill \\ \hfill {\displaystyle a^2=-b^2+2x^2\mathrm{,}}\hfill \end{array}}$ amivel egyenértékű, hogy $\begin{array}{c}{\displaystyle x^2=\frac{a^2+b^2}{2}\mathrm{,}\text{vagyis}x=\sqrt[]{\frac{a^2+b^2}{2}}\mathrm{.}}\end{array}$ Ezzel a bizonyítás végére értünk, megmutattuk, hogy $x$ éppen $a$ és $b$ négyzetes közepével egyenlő. $b)$ Legyen a trapéz nagyobb alapjának hossza $z$. Felhasználva az $a)$ feladatrész eredményét, felírjuk és megoldjuk az alábbi egyenletet $\begin{array}{c}{\displaystyle \sqrt[]{\frac{5^2+z^2}{2}}=45\iff z^2=2\cdot {45}^2-5^2=4025\iff z=\sqrt[]{4025}\text{cm}\mathrm{.}}\end{array}$ A trapéz másik alapja $\sqrt[]{4025}$ cm hosszúságú.