Cím:	Gyakorló feladatsor emelt szintű matematikai érettségire
Szerző(k):	Kozma Katalin Abigél, Győr
Füzet:	2024/szeptember, 328 - 330. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Kedves Olvasók! Ezek a feladatsorok azért készülnek, hogy felkészülési lehetőséget biztosítsanak az írásbeli érettségire azoknak, akik emelt szintű vizsgát kívánnak tenni. A feladatsorokat tapasztalt tanárok állítják össze, köztük olyanok is, akik maguk is részt vesznek az érettségi feladatok összeállításában. Az idei tanévtől lehetőségetek van beküldeni a megoldásotokat az emeltkomal@gmail.com címre. A beérkezett dolgozatokat kijavítjuk és visszaküldjük, így is segítve a felkészüléseteket. (A beküldéssel kapcsolatos technikai tudnivalókat a feladatsor végén találod meg.) A legszorgalmasabb, illetve legeredményesebb beküldők között a tanév végén KöMaL ajándéktárgyakat sorsolunk ki. Sikeres felkészülést kívánunk! I. rész     1. $a)$ Oldjuk meg az $\text{log}{}_x\left(64x^2\right)=-4$ egyenletet a pozitív valós számok halmazán. (5 pont) $b)$ Oldjuk meg a ${\displaystyle \frac{\left(2x+14\right)\left(x-2\right)}{\left(x-7\right)\left(x+5\right)}}>2$ egyenlőtlenséget a valós számok halmazán. 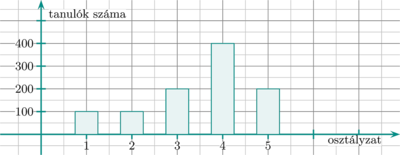(7 pont)   2. Egy középiskola tanulói az elmúlt tanév végén matematikából az alábbi oszlopdiagramon szemléltetett osztályzatokat szerezték: $a)$ Számítsuk ki az osztályzatok szórását. (5 pont) $b)$ Készítsünk dobozdiagramot az adatok szemléltetésére. (7 pont)     3. Három pozitív egész szám szorzata $33339600$. Az elsőt $3$-mal, a másodikat $4$-gyel, a harmadikat $5$-tel megszorozva ugyanazt a számot kapjuk. $a)$ Melyek ezek a számok? (5 pont) Egy paralelogramma átlói által közbezárt szög nagysága ${77}^{\circ }17\text{'}$, az átlók hossza $386\text{cm}$ és $42\text{dm}$. $b)$ Adjuk meg (egészre kerekítve) a paralelogramma oldalainak centiméterben mért hosszát. (7 pont)   4. $a)$ Ábrázoljuk az $f:\left]-3;3\right[\to \text{R}$; $f\left(x\right)=\left|{\left({\displaystyle \frac{1}{5}}\right)}^{x+2}-1\right|$ függvény grafikonját koordináta-rendszerben, és adjuk meg $f$ értékkészletét. (6 pont) $b)$ Határozzuk meg az $f$ értelmezési tartományának azon elemeit, amelyekre $f\left(x\right)=\mathrm{0,}8$. (6 pont) $c)$ Hol metszi az $f$ függvény grafikonja az $y$-tengelyt? (3 pont)   II. rész   5. Egy derékszögű háromszög oldalhosszai számtani sorozatot alkotnak (azaz a hosszabb befogó ugyanannyival nagyobb a rövidebb befogónál, amennyivel az átfogó hosszabb nála). $a)$ Hányszorosa a háromszög köré írt kör területe a háromszögbe írható kör területének? (8 pont) $b)$ A háromszög átfogójához tartozó magasságának hossza $24$ egység. Mekkora a háromszög kerülete? (4 pont) $c)$ Adott az $a_n={\displaystyle \frac{42n^3-24n+2000}{6n^2-100}}$ sorozat. Konvergens-e ez a sorozat? Indokoljuk válaszunkat. (4 pont)   6. Legyen $T$ azon $12$-jegyű pozitív egész számok halmaza, amelyek tízes számrendszerbeli alakjában legalább egyszer szerepel a $2024$ blokk. ($T$ eleme például a $120245678900$ és a $202477772024$, viszont nem eleme az $520022444202$.) $a)$ Hány elemű a $T$ halmaz? (8 pont) $b)$ Pistike a $T$ halmazból véletlenszerűen kiválaszt egyszerre három számot. Mekkora a valószínűsége, hogy mindhárom szám $1$-nél többször tartalmazza a $2024$ blokkot? (5 pont) $c)$ Móricka a $T$ halmazból véletlenszerűen visszatevéssel választ ki három számot. Mekkora a valószínűsége, hogy mindhárom szám $1$-nél többször tartalmazza a $2024$ blokkot? (3 pont)   7. $a)$ Határozzuk meg az alábbi állítások logikai értékét. Indokoljuk válaszunkat. (8 pont) A: Van olyan függvény, amelyet négyszer egymás után deriválva önmagát kapjuk. B: Ha egy függvény folytonos egy pontban, akkor abban a pontban differenciálható. C: Ha egy függvénynek egy pontban az első és a második deriváltja is nulla, akkor abban a pontban inflexiós pontja van. $b)$ Fogalmazzuk meg az előző feladatrész B állításának megfordítását és állapítsuk meg a megfordítás logikai értékét. (Indoklás nem szükséges.) (3 pont) $c)$ Fogalmazzuk meg a $b)$ feladatrész megoldásaként leírt állítás tagadását. (2 pont) $d)$ Fogalmazzuk meg az $a)$ feladatrész C állításának megfordítását és állapítsuk meg a megfordítás logikai értékét. (Indoklás nem szükséges.) (3 pont)   8. Adott a $k_1:x^2+y^2-20x+10y-19=0$ egyenletű kör. A $k_2$ kör kerülete a $k_1$ kör kerületénél ennek $75\%$-ával kisebb. A két kör koncentrikus. $a)$ Írjuk fel a $k_2$ kör egyenletét. (5 pont) $b)$,Mutassuk meg, hogy a $P\left(10;-2\right)$ pont illeszkedik a $k_1$ vagy a $k_2$ körre. (3 pont) $c)$ Határozzuk meg a $k_2$ kör $Q\left(7;-5\right)$ pontjában húzott érintőegyenesének egyenletét. (5 pont) A $k_1$ kör belsejében véletlenszerűen kiválasztunk egy pontot. $d)$ Mekkora a valószínűsége, hogy a kiválasztott pont a $k_2$ körön kívül van, ha a körön bármely alakzat eltalálásának valószínűsége egyenesen arányos annak területével? (3 pont)   9. $a)$ Bizonyítsuk be, hogy bármely trapéz területét felező, az alapokkal párhuzamos szakasz hossza éppen az alapok négyzetes közepével egyenlő. (11 pont) $b)$ Egy trapéz egyik alapjának hossza $5\text{cm}$, a trapéz területét felező, az alapokkal párhuzamos szakasz hossza $45\text{cm}$. Számítsuk ki a másik alap hosszának pontos értékét. (5 pont) Kozma Katalin Abigél Győr     Technikai tudnivalók a beküldéshez A megoldásodat az emeltkomal@gmail.com címre küldheted be, a határidő a feladatsor megjelenését követő hónap 7. napja. A megoldást szkennelve vagy fényképezve, lehetőség szerint egyetlen pdf file-ban mellékeld a leveledhez. A megoldás leírásakor és szkennelésekor/fényképezésekor is ügyelj a jól olvashatóságra! Ha a kép felbontása 200 dpi, akkor az általában megfelelő. A dolgozatból egyértelműen derüljön ki, hogy ki készítette, tehát tüntesd fel az elején a nevedet, iskoládat, osztályodat! A kijavított dolgozatot arra a címre küldjük vissza, ahonnan az eredeti érkezett.