Cím:	Megoldásvázlatok a 2023/9. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Kozma Katalin Abigél, Győr
Füzet:	2024/január, 14 - 21. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg a $\begin{array}{c}{\displaystyle \text{lg}\left(2025-x^2\right)<\sqrt[2024]{x-2023}}\end{array}$ egyenlőtlenséget a valós számok halmazán. (6 pont) $b)$ Oldjuk meg a $\begin{array}{c}{\displaystyle \frac{42-x}{x-1}-\frac{2x-20}{2-x}=2}\end{array}$ egyenletet a valós számok halmazán. (6 pont)   Megoldás. $a)$ Meghatározzuk az egyenlőtlenség értelmezési tartományát. A logaritmus definíciója miatt $2025-x^2>0$, amiből $-45<x<45$, a $2024.$ gyök miatt pedig $x-2023\ge 0$, azaz $x\ge 2023$. A két halmaz metszete üres, így nincs olyan valós szám, amelyre az egyenlőtlenség mindkét oldala értelmezhető, tehát a megoldáshalmaz $M=\varnothing$. $b)$ Az egyenlet értelmezési tartománya: $\text{R}\setminus \left\{1;2\right\}$. Azonos átalakítások, majd rendezés után az $x^2-28x+68=0$ másodfokú egyenlethez jutunk, melynek két valós gyöke $x_1=14+8\sqrt[]{2}$ és $x_2=14-8\sqrt[]{2}$. Mindkét gyök eleme az értelmezési tartománynak, így az eredeti egyenletnek is megoldásai.   2. A híres Dávid-szobor Firenzében egy állandó kiállításon látható. Biztonsági okokból a szobor egy $2\mathrm{,}3$ méter magas talapzaton áll. A talapzat aljától pontosan $4\mathrm{,}5$ méterre található padlókamerából a szobor legalsó pontja ${32}^{\circ }$-kal kisebb emelkedési szögben látszik, mint a legfelső pontja. $a)$ Hány centiméter magas a szobor? (7 pont) Egy pénteki napon $2650$ felnőtt-, és $1100$ gyermekjegyet értékesített a múzeum, így aznap $37750$ euró folyt be a jegyekből. Másnap $2830$ felnőtt-, és $4500$ gyermekjegyet adtak el, ezzel $50290$ euró lett az aznapi jegybevétel. $b)$ Számítsuk ki egy felnőtt-, illetve egy gyermekjegy árát. 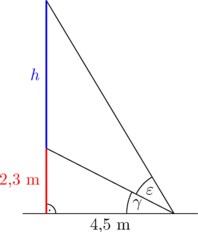(7 pont)     Megoldás. $a)$ Készítsünk ábrát, jelöljük a szobor magasságát $h$-val.     Adott $\epsilon ={32}^{\circ }$. A $\gamma$ hegyesszöget tartalmazó derékszögű háromszög két ismert befogójából $\text{tg}\gamma ={\displaystyle \frac{2\mathrm{,}3}{4\mathrm{,}5}}$, amiből $\gamma \approx {27}^{\circ }$. Ekkor $\gamma +\epsilon \approx {59}^{\circ }$, így $\text{tg}{59}^{\circ }\approx {\displaystyle \frac{h+2\mathrm{,}3}{4\mathrm{,}5}}$, amit $h$-ra megoldva kapjuk, hogy $h\approx 5\mathrm{,}19$ méter. A szobor magassága $519$ centiméter. $b)$ Jelöljük a felnőttjegy árát $x$-szel, a gyermekjegyét pedig $y$-nal. A feladat feltételei alapján felállítjuk a $\{$ 2650x+1100y=377502830x+4500y=50290 egyenletrendszert, amelyet megoldhatunk a behelyettesítő vagy az egyenlő együtthatók módszerével is. A megoldás: $x=13$ és $y=3$, azaz a felnőttjegy $13$, míg a gyermekjegy $3$ euróba kerül.   3. A trícium, azaz a hármas hidrogénizotóp mennyiségének a fele $12\mathrm{,}3$ év alatt bomlik el. $a)$ Mennyi idő alatt bomlik el adott mennyiségű trícium $\frac{15}{16}$ része? (3 pont) $b)$ Egy palack idei bor $350$ százalékkal több tríciumot tartalmaz, mint egy ‐ ugyanakkora űrtartalmú ‐ palack ugyanolyan, múlt századi bor. Hány éves lehet a régebbi bor a tríciumtartalma alapján? (8 pont)   Megoldás. $a)$ Ha a trícium eredeti mennyisége $x>0$ mólnyi atom, akkor $t$ év alatt elbomlik ${\displaystyle \frac{15}{16}}\cdot x$ mólnyi, így megmarad $x-{\displaystyle \frac{15}{16}}\cdot x={\displaystyle \frac{1}{16}}\cdot x$ mólnyi, a felezési idő alapján pedig tudjuk, hogy $12\mathrm{,}3$ évenként feleződik a mennyisége. Ezek alapján felírhatjuk, hogy $\begin{array}{c}{\displaystyle x\cdot {\left({\displaystyle \frac{1}{2}}\right)}^{\frac{t}{12\mathrm{,}3}}={\displaystyle \frac{x}{16}}\mathrm{,}}\end{array}$ amiből $x$-szel való egyszerűsítés után, majd az ${\displaystyle \frac{1}{2}}$ alapú exponenciális függvény szigorú monotonitását felhasználva azt kapjuk, hogy ${\displaystyle \frac{t}{12\mathrm{,}3}}=4$, azaz $t=49\mathrm{,}2$ év alatt bomlik el a trícium ${\displaystyle \frac{15}{16}}$ része. $b)$ Az idei bor tríciumtartalma $100+350=450$ százaléka, azaz $4\mathrm{,}5$-szerese a régebbi bor tríciumtartalmának. Az utóbbit $y$-nal jelölve teljesül, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y}& {\displaystyle =4\mathrm{,}5y\cdot {\left(\frac{1}{2}\right)}^{\frac{t}{12\mathrm{,}3}}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{1}{4\mathrm{,}5}}& {\displaystyle ={\left(\frac{1}{2}\right)}^{\frac{t}{12\mathrm{,}3}}\mathrm{,}}\hfill \end{array}}$ amiből $t=12\mathrm{,}3\cdot \text{log}{}_{\frac{1}{2}}\left(\frac{1}{4\mathrm{,}5}\right)\approx 26\mathrm{,}7$ év, azaz a régebbi bor hozzávetőlegesen $27$ éves (így valóban a XX. században készülhetett.)   4. $a)$ Tornaórán egy $12$ fős csoport medicinlabdával erősített. Az egyik gyakorlat során mindenki háromszor dobott és a tanár a legnagyobb dobás hosszát méterben feljegyezte. A testnevelő megállapította, hogy a felírt számok terjedelme $5$, mediánja és módusza is $9$ méter. Alsó kvartilise $8\mathrm{,}1$ méter, felső kvartilise pedig $10\mathrm{,}5$ méter. Adjunk meg három különböző adathalmazt, amelyre a fenti megállapítások érvényesek. (6 pont) $b)$ Robinak óra után 12 azonos méretű labdát kell két dobozba beraknia, az egyikben 4, a másikban 8 labda fér el. A labdák közül 7 piros, 3 kék, a többi zöld színű. Hányféleképpen helyezheti el a labdákat Robi, ha az azonos színű labdákat nem különbözteti meg és dobozon belül a labdák elhelyezkedése nem számít? (8 pont)   Megoldás. $a)$ Ha $12$ elemű az adathalmaz, akkor növekvő sorrend szerint a két középső elem számtani közepe a medián, az első hat elem mediánja egyenlő az alsó kvartilissel, a második hat elem mediánja pedig a felső kvartilist adja. Mivel a módusz is $9$, ezért a két középső elem mindenképpen $9$ kell, hogy legyen, de akár $4$-szer, illetve $6$-szor is szerepeltethetjük. A terjedelem is adott, tehát figyeljünk, hogy a legnagyobb és a legkisebb elem különbsége $5$ legyen. Az előzőek alapján megfelelőek például az alábbi adathalmazok (az elemek méterben értendők): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A_1}& {\displaystyle =\left\{6\mathrm{,}2;6\mathrm{,}5;8;8\mathrm{,}2;8\mathrm{,}5;9;9;9\mathrm{,}5;10;11;11\mathrm{,}1;11\mathrm{,}2\right\}\mathrm{,}}\hfill \\ \hfill {\displaystyle A_2}& {\displaystyle =\left\{6;8;8;8\mathrm{,}2;9;9;9;9;10;11;11;11\right\}\mathrm{,}}\hfill \\ \hfill {\displaystyle A_3}& {\displaystyle =\left\{7;7;7\mathrm{,}2;9;9;9;9;9;9;12;12;12\right\}\mathrm{.}}\hfill \end{array}}$ $b)$ Két darab zöld labda van. Nézzük meg, hogy a kisebb dobozba hány zöld és hány kék kerül, amely már egyértelműen meghatározza az elhelyezést (hiszen a maradékot kitöltjük pirosakkal). Zöldből lehet $\mathrm{0,1}$ vagy $2$, ami $3$ lehetőség. Kékből pedig $0$, $1$, $2$ vagy $3$ lehet, ami $4$ lehetőség, ez összesen $3\cdot 4=12$ lehetőség lenne, de ezek közül nem jó, ha két zöld és három kék kerülne bele, mert öt labda nem fér el a kisebb dobozban. Összesen $12-1=11$ lehetőség van a labdák elhelyezésére.   II. rész   5. Egy $28$ fős osztályban a matematikatanár háromféleképpen mérte fel a tanulók decemberi teljesítményét: videós beszámoló, interaktív feladatlap, illetve írásbeli dolgozat formájában. Minden tanuló részt vett legalább egyfajta értékelésben. Tudjuk, hogy $15$-en videóztak, ugyanennyien pedig pontosan kétfajta értékelés résztvevői voltak. $16$-an interaktív feladatokat oldottak meg, $22$-en pedig dolgozatot írtak. A tanár találomra kiválaszt egy tanulót, akit szóban is szeretne feleltetni. $a)$ Mekkora a valószínűsége, hogy olyan tanulót választ, aki mindhárom értékelésben részt vett decemberben? (9 pont) $b)$ Az osztály tanulóinak hány százaléka vett részt mindössze egyfajta értékelésben? 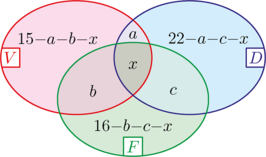(2 pont) $c)$ Legfeljebb hányan lehetnek azok, akik csak dolgozatot írtak? (5 pont)   Megoldás. $a)$ Jelöljük $x$-szel azoknak a tanulóknak a számát, akik mindhárom említett értékelésben részt vettek, és készítsünk Venn-diagramot:     A létszámokat összeadva éppen $28$-at kapunk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 28}& {\displaystyle =15-a-b-x+a+b+c+x+22-a-c-x+16-b-c-x\mathrm{,}}\hfill \\ \hfill {\displaystyle 2x}& {\displaystyle =25-a-b-c\mathrm{.}}\hfill \end{array}}$ Tudjuk, hogy pontosan két értékelésben $15$ tanuló vett részt, ezért $a+b+c=15$, ezt behelyettesítve a fent kapott egyenletbe: $2x=25-15$, amiből $x=5$, azaz öt tanuló szerepelt mindhárom értékelésen. A kiválasztás valószínűsége $p={\displaystyle \frac{5}{28}}$. $b)$ Az $a)$ feladatrészben láttuk, hogy öten mindhárom értékelésben részt vettek, az pedig adott, hogy tizenöten pontosan kétfajta értékelési fajtában voltak érintettek, így $28-\left(5+15\right)=8$-an vannak, akik csak egyfajta számonkérésen voltak. Ez az osztálylétszám ${\displaystyle \frac{8}{28}\cdot 100}\approx 28\mathrm{,}57$ százaléka. $c)$ Az előző feladatrészben láttuk, hogy $8$ tanuló pontosan egyfajta értékelés résztvevője volt. Előfordulhatott, hogy mind a nyolcan dolgozatot írtak, ez esetben egyetlen olyan tanuló sem volt, aki csak videós beszámolót készített, illetve olyan sem volt, aki interaktív feladatlapot töltött ki. Ez tényleg megvalósulhat például az 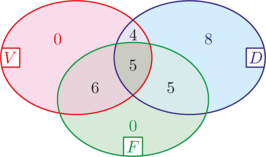    Legfeljebb $8$ olyan tanuló volt, aki kizárólag dolgozatot írt decemberben.   6. Egy $0\mathrm{,}4$ dm átmérőjű tömör fémgömböt legurítottak egy golyópályán. A táv első felében $0\mathrm{,}12$ m/s, a második felében $0\mathrm{,}16$ m/s átlagsebességgel gurult a gömb. $a)$ Mekkora volt a gömb (a pálya teljes hosszára vonatkozó) átlagsebessége? (10 pont) Ezután a gömböt megolvasztották és anyagából $0\mathrm{,}5$ cm sugarú tömör gömböket öntöttek. $b)$ Hány darab ilyen gömb keletkezhetett az öntés során? (6 pont)   Megoldás. $a)$ Legyen a táv hossza $x$, ekkor az első felét ${\displaystyle \frac{x}{2\cdot 0\mathrm{,}12}}$ idő alatt teszi meg, a második felét ${\displaystyle \frac{x}{2\cdot 0\mathrm{,}16}}$ idő alatt, így az átlagsebessége $\begin{array}{c}{\displaystyle v_{\text{átlag}}=\frac{x}{\frac{x}{2\cdot 0\mathrm{,}12}+\frac{x}{2\cdot 0\mathrm{,}16}}=\frac{24}{175}\approx 0\mathrm{,}137\text{m}/\text{s}\mathrm{.}}\end{array}$ $b)$ A gömb sugara $2\text{cm}$, ezért a gömb térfogata $V_1={\displaystyle \frac{4}{3}\cdot 2{}^3\cdot \pi }{\text{cm}}^3$, a kisebb gömb sugara $0\mathrm{,}5$ centiméter, így térfogata $V_2=\frac{4}{3}\cdot 0\mathrm{,}{5}^3\cdot \pi {\text{cm}}^3$. Ezek aránya megmutatja, hogy elvileg hány kisebb gömb készíthető a nagyobb gömb anyagából: $\begin{array}{c}{\displaystyle \frac{V_1}{V_2}=\frac{\frac{4}{3}\cdot 2^3\cdot \pi }{\frac{4}{3}\cdot {0\mathrm{,}5}^3\cdot \pi }=\mathrm{64,}}\end{array}$ azaz legfeljebb $64$ darab kisebb gömb önthető a nagyobb gömbből.   7. Gergő a $180$-nál kisebb, $6$-tal osztható természetes számok mindegyikét felírta egy-egy cetlire, majd a cetliket belerakta egy nagy dobozba. $a)$ Mennyi a cetliken szereplő számok összege, illetve szorzata, ha minden cetlire különböző számot írt Gergő? (4 pont) Gergő öccse találomra kiválasztott a cetlik közül egyszerre éppen hármat. $b)$ Mekkora a valószínűsége, hogy legalább két kiválasztott cetlin $10$-zel osztható szám szerepel? (5 pont) Ezután Gergő visszatette az összes cetlit a dobozba, jól megkeverte őket, majd véletlenszerűen kiválasztott egy cetlit, felírta a rajta lévő számot, majd ismét visszatette a dobozba. Ezt az eljárást még kétszer megismételte, tehát összesen három számot írt fel. $c)$ Mekkora a valószínűsége, hogy Gergő nem írta fel a nulla számjegyet? (7 pont)   Megoldás. $a)$ A cetlik száma $30$, hiszen $0$-tól $174$-ig minden hatodik egész szám éppen egy cetlin szerepel. A számok szorzata $0$, mert az egyik tényező $0$. A számok egy $d=6$ differenciájú számtani sorozat egymást követő tagjai, ezért az összegük $\begin{array}{c}{\displaystyle S_{30}=\frac{0+174}{2}\cdot 30=2610.}\end{array}$ $b)$ A $6$ és a $10$ legkisebb közös többszöröse a $30$, ezért a cetliken szereplő számok közül azok oszthatók $10$-zel, amelyek $30$-cal is. Összesen hat ilyen szám van: $0$; $30$; $60$; $90$; $120$; $150$. Kedvező esetben vagy éppen két ilyen számot választott ki Gergő öccse, vagy mindhármat ezek közül választotta, ez $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{6}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{24}{1}\right)+\left(\genfrac{}{}{0ex}{}{6}{3}\right)=360+20=380}\end{array}$ kedvező esetet jelent. A $30$ különböző elemből egyszerre vett ki hármat, így összesen $\left(\genfrac{}{}{0ex}{}{30}{3}\right)=4060$ eset van. A keresett valószínűség $p={\displaystyle \frac{380}{4060}}={\displaystyle \frac{19}{203}}\approx 0\mathrm{,}0936$. $c)$ A $10$-zel osztható számokon kívül még azok is tartalmaznak nulla számjegyet, amelyeknek a középső számjegyük $0$, a cetliken lévők közül ilyen a $102$ és a $108$, azaz összesen nyolc olyan cetli van, amelyen szerepel a nulla számjegy. Ha Gergő egyszer sem írta le a nullát, akkor mindhárom alkalommal abból a $22$ darab számból választott, amelyben nincs nulla. Ennek valószínűsége $p={\left({\displaystyle \frac{22}{30}}\right)}^3={\displaystyle \frac{1331}{3375}}\approx 0\mathrm{,}394$.   8. $a)$ Egy kör két párhuzamos húrja $4$ cm és $198$ mm hosszúságú. Mekkora lehet a köztük lévő távolság, ha a kör átmérőjének hossza $20\mathrm{,}2$ cm? (8 pont) $b)$ Egy derékszögű háromszög külső szögeinek ívmértéke ‐ nagyság szerint sorba állítva ‐ egy mértani sorozat három, közvetlenül egymást követő tagja. Adjuk meg a háromszög belső szögeinek fokmértékét. 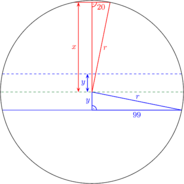(8 pont)   Megoldás. $a)$ Tekintsük az alábbi ábrát, amelyen a kör sugarát $r$-rel jelöltük.     A kör sugarának hossza $101$ mm. Minden húr felezőmerőlegese átmegy a kör középpontján, ezért használhatjuk a Pitagorasz-tételt. A $40$ mm-es húr távolsága a kör középpontjától $x=\sqrt[]{{101}^2-{20}^2}=99$ mm. A $198$ mm-es húr távolsága a kör középpontjától $y=\sqrt[]{{101}^2-{99}^2}=20$ mm. A húrok párhuzamosak, így kétféle távolság léphet fel: ha azonos félkörben vannak, akkor $x-y=99-20=79$ mm, ha pedig különböző félkörben vannak, akkor $x+y=99+20=119$ mm. $b)$ A szögek ívmértéke és fokmértéke egyenesen arányos, ezért a feladat feltételei a háromszög külső szögeinek fokmértékére is fennállnak. Egy derékszögű háromszög legnagyobb belső szöge $90$ fokos, így ugyanekkora a legkisebb külső szöge. Legyen a mértani sorozat hányadosa $q>1$, ekkor a külső szögek nagysága $\gamma \text{'}={90}^{\circ }$, $\beta \text{'}=q\cdot {90}^{\circ }$, $\alpha \text{'}=q^2\cdot {90}^{\circ }$, amelyeknek összege ${360}^{\circ }$. ${\displaystyle \begin{array}{c}\hfill {\displaystyle q^2\cdot {90}^{\circ }+q\cdot {90}^{\circ }+{90}^{\circ }={360}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle q^2+q-3=\mathrm{0,}\text{ebből}{q}_{\mathrm{1,2}}={\displaystyle \frac{-1\pm \sqrt[]{13}}{2}}\mathrm{.}}\hfill \end{array}}$ Láthatjuk, hogy $q_1>1$, így ebből jó megoldást kapunk: $\begin{array}{c}{\displaystyle \gamma \text{'}={90}^{\circ }\mathrm{,}\beta \text{'}\approx 117\mathrm{,}{25}^{\circ }\mathrm{,}\alpha \text{'}\approx 152\mathrm{,}{75}^{\circ }\mathrm{,}}\end{array}$ tehát a háromszög belső szögeinek fokmértéke: $\begin{array}{c}{\displaystyle \gamma ={90}^{\circ }\mathrm{,}\beta \approx 62\mathrm{,}{75}^{\circ }\mathrm{,}\alpha \approx 27\mathrm{,}{25}^{\circ }\mathrm{.}}\end{array}$   9. Adott a következő két halmaz: $\begin{array}{c}{\displaystyle A=\left\{x\in \text{N}\mid x^2<9\right\}\text{és}B=\left\{\text{egyjegyű, pozitív prímszámok}\right\}\mathrm{.}}\end{array}$ Hány olyan ‐ egymástól különböző ‐ függvény van, amelynek $a)$ értelmezési tartománya az $A$, képhalmaza a $B$ halmaz? (4 pont)   $b)$ értelmezési tartománya az $A$, értékkészlete a $B$ halmaz? (4 pont)   $c)$ értelmezési tartománya a $B$, képhalmaza az $A$ halmaz? (4 pont)   $d)$ értelmezési tartománya a $B$, értékkészlete az $A$ halmaz? (4 pont)   Megoldás. A két halmaz az elemeivel felírva: $A=\left\{0;1;2\right\}$ és $B=\left\{2;3;5;7\right\}$. $a)$ Az $A$ halmaz minden eleméhez hozzárendelhetjük a $B$ halmaz bármelyik elemét, ez összesen $4^3=64$ különböző függvényt jelent. $b)$ Egy függvény értékkészletének elemszáma nem lehet nagyobb, mint az értelmezési tartomány elemszáma, így az ilyen függvények száma $0$. $c)$ A $B$ halmaz mind a négy eleméhez $3$‐$3$ elemből választhatunk, ezért $3^4=81$ különböző függvényt hozhatunk létre. $d)$ Az értelmezési tartomány $4$ eleméből kiválasztjuk azt a kettőt, amelyhez az $A$ halmaznak ugyanazt az elemét rendeljük, ezt $\left(\genfrac{}{}{0ex}{}{4}{2}\right)=6$-féleképpen tehetjük meg. A másik két elemhez pedig az $A$ halmaz másik két elemét rendeljük, így az $A$ halmaz összes elemét felhasználjuk. Az értékkészlet három elemét $3!=6$ különböző sorrendben rendelhetjük a $B$ halmaz megfelelő elemeihez, így a feltételeknek megfelelő függvények száma: $\left(\genfrac{}{}{0ex}{}{4}{2}\right)\cdot 3!=6\cdot 6=36$. Megjegyzés. Komplementer módszerrel is számolhatunk. A $c)$ feladatrészben kapott függvények közül azok nem jók, amelyekben nem választottuk ki az $A$ halmaz mindhárom elemét, ezért alkalmazhatjuk a logikai szita formulát. A  $d)$ feladatrész feltételeinek megfelelő függvények száma $3^4-3\cdot 2^4+3\cdot 1^4=36$.