Cím:	Beszámoló a 7. Európai Fizikai diákolimpiáról
Szerző(k):	Szász Krisztián ,  Vankó Péter
Füzet:	2023/október, 425 - 431. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Beszámoló a 7. Európai Fizikai Diákolimpiáról   Idén 2023. június 16. és 20. között Hannoverben, Németországban rendezték meg az Európai Fizikai Diákolimpiát (EuPhO). A versenyen 28 európai és 9 Európán kívüli ország összesen 173 diákja vett részt. A versenyen 18 aranyérmet osztottak ki, amelyből az egyiket egy magyar diák, Molnár-Szabó Vilmos szerezte meg, aki az abszolút 11. helyen végzett. A csapat és eredményeik: Molnár-Szabó Vilmos (Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, 12. oszt.) aranyérem (27,8 pont), felkészítő tanára: Nagy Piroska Mária; Fey Dávid (Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, 12. oszt.) bronzérem (19,3 pont), felkészítő tanára: Nagy Piroska Mária; Bencz Benedek (Baár-Madas Református Gimnázium, Általános Iskola és Diákotthon, 10. oszt.) bronzérem (18,3 pont), felkészítő tanára: Horváth Norbert; Budai Csanád Gyula (Deák Téri Evangélikus Gimnázium, 12. oszt.) bronzérem (16,0 pont), felkészítő tanára: Horváth Gabriella; Molnár Barnabás (Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, 12. oszt.) (11,1 pont), felkészítő tanára: Nagy Piroska Mária. A magyar csapat vezetői Szász Krisztián és Vankó Péter voltak, Vigh Máté pedig a zsűriben, a harmadik elméleti feladat szerzőjeként képviselte hazánkat. Az alábbiakban közöljük a verseny feladatait, a megoldások a verseny honlapján érhetők el: https://eupho.ee/eupho-2023/.   Kísérleti feladatok 1. Mágneses inga (10 pont) Egy inga rezgési frekvenciája módosítható az inga és a tartója közötti mágneses erőkkel. Ebben a kísérletben egy olyan ingamozgást fogsz vizsgálni, amely gravitációs és mágneses kölcsönhatások együttes potenciáljában történik, a 3. ábrán látható mérési elrendezésben.   Eszközök (lásd a 3. ábrát is) A ‐ Ingatest pontszerű támaszokkal és tükörrel a szögméréshez.   B ‐ Ingatorony az inga alátámasztására szolgáló rögzített pontokkal és lézermodullal a szögméréshez.   C ‐ A külső mágneseket tartó sín.   D ‐ 2 kis dipólmágnes, amit az ingatestre lehet rögzíteni (lehet zöld, piros, fehér vagy sárga).   E ‐ 2 egyforma külső dipólmágnes (fekete).   F ‐ 2 ismeretlen külső mágnes, F1 és F2 (F1 kék, F2 fehér pöttyel van megjelölve a végein).   G ‐ Ernyő a lézerfoltnak a szögmérésnél.   H ‐ Stopper.   I ‐ Ragasztószalag, az ingatorony asztalhoz rögzítéséhez.   J ‐ Ceruza és vonalzó.   1.1 Tömegek (1 pont) Az ingatest (pendulum) és a rá rögzített két kis dipólmágnes teljes tömege $M_{\text{pen}}+M_{\text{mag}}=52\mathrm{,}3\pm 0\mathrm{,}2\text{g}$. Határozd meg $M_{\text{pen}}$ és $M_{\text{mag}}$ értékét a lehető legpontosabban!   1.2 Mágneses dipólmomentumok (4 pont) Ha külső mágnesek vannak a közelben, a mágneses inga a gravitációs és mágneses kölcsönhatás együttes potenciáljában mozog. Az inga ilyenkor kialakuló $\omega$ frekvenciája felírható az ${\omega }_1$ sajátfrekvencia és az ${\omega }_{\text{mag}}$ ,,mágneses frekvenciaeltolódás'' függvényeként: $\begin{array}{c}{\displaystyle {\omega }^2={\omega }_1^2\pm {\omega }_{\text{mag}}^2\mathrm{.}}\end{array}$ (1) Abban az esetben, ha a két fekete külső dipólmágnes szimmetrikusan van elhelyezve az inga egyensúlyi helyzetétől $d$ távolságra (lásd az 1. ábrát) és a rezgés amplitúdója kicsi, a frekvenciaeltolódás: $\begin{array}{c}{\displaystyle {\omega }_{\text{mag}}^2=\frac{6{\mu }_0}{I\pi }\cdot j_1\cdot j_2\cdot \frac{{\ell }^2}{d^5}\mathrm{,}}\end{array}$ (2) ahol ${\mu }_0=4\pi \cdot {10}^{-7}\text{N/<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>A</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$ a vákuum permeabilitása, $I$ a mágneses inga tehetetlenségi nyomatéka a forgástengelyre vonatkoztatva, $j_1$ az ingán lévő mágnesek összesített mágneses momentuma, $j_2$ az egyes külső mágnesek mágneses momentuma és $\ell$ az ingán lévő mágnes távolsága a forgástengelytől. A dipólusmomentumok relatív erősségére vonatkozóan felteheted, hogy $j_2=2\mathrm{,}4\cdot j_1$. A nehézségi gyorsulás $g=9\mathrm{,}81\text{m/<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>s</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$.     1. ábra. Frekvenciaeltolódás külső mágnesek segítségével (felülnézet). A külső mágnesek iránya megfordítható   $a)$ Mérd meg az inga frekvenciáját a mágnesek közötti $d$ távolság függvényében! Használj nagyon kis amplitúdót. Mérd végig a teljes lehetséges frekvenciatartományt. $b)$ Határozd meg az ingamágnesek és a külső mágnesek anyagának ,,átlagos mágnesezettségét'' (egységnyi tömegre vonatkoztatott mágneses momentumát)! Ehhez készíts egy megfelelő grafikont. További mérésekre is szükséged lehet, hogy minden ismeretlent meghatározzál. A mágnesek nem-mágneses burkolatának vastagságát és tömegét elhanyagolhatod.   1.3 Ismeretlen külső mágnesek (3 pont) Mindkét kék, ismeretlen külső mágnes (F1 és F2) több mágneses dipólusból van összeállítva. F1 belsejében minden dipólus pont fordítva van, mint F2 belsejében. A mágneses frekvenciaeltolódás az 1. ábrának megfelelő elrendezés esetén hatványfüggést követ:   $\begin{array}{c}{\displaystyle {\omega }_{\text{mag,F}}^2\sim d^{\alpha }\mathrm{.}}\end{array}$   (3) $a)$Mérdmegaz ingafrekvenciáját$d$függvényében!Használjnagyonkisamplitúdót.Olyanelrendezésthasználj,hogya mágnesesfrekvenciaeltolódásta lehetőlegpontosabbantudjadmeghatározni.   $b)$ Határozd meg az $\alpha$ kitevőt!   $c)$ Vázold fel a mágneses dipólusok egy lehetséges elrendezését az F1 és F2 belsejében, és indokold meg a választásod!   1.4 Nemlineáris inga (2 pont) Térj vissza az 1.2 részben használt elrendezéshez a fekete külső dipólmágnesekkel, az 1. ábrának megfelelő elrendezésben! Az (1) képlet alapján a kis amplitúdójú inga frekvenciája teljesen eltüntethető, $\omega \to 0$.   $a)$ Határozd meg a lehető legpontosabban azt a mágnesek közötti $d$ távolságot, amely a teljes eltüntetéshez szükséges!   $b)$ Vizsgáljad az inga periódusidejének amplitúdótól való függését abban az esetben, amikor az előbbi eltüntetést a lehető legjobban sikerült beállítanod! Javasolj egy függvényt a kapcsolatra, és igazold ezt a mért adataiddal. Diszkutáld az esetleges eltérések okát.   2. Optikai feketetdoboz (10 pont) Feladatod, hogy meghatározd egy optikai feketedoboz tartalmát anélkül, hogy kinyitnád azt. A feketedoboz négy optikai nyílással ($A$, $B$, $C$ és $D$) rendelkezik a megvilágításhoz, és két optikai tengelye van (2. ábra). Az optikai tengelyek merőlegesek egymásra. Mindegyik nyílás mögött legfeljebb egy optikai elem van, valamint egy a doboz közepén is. Egy lézert és egy kerékkel ellátott lézertartót (amire ceruzával jelöléseket tehetsz) használhatsz; a lézert a kerékkel tudod forgatni.   Eszközök (lásd a 4. ábrát) A ‐ Feketedoboz.   B ‐ Lézeregység kerékkel ellátott tartóban (mindkét feladathoz használd ugyanazt a lézeregységet, amit az asztalra kell tenni).   C ‐ Átlátszó elem.   D ‐ Ragasztószalag, ceruza, vonalzó, papírdarab átlós skálával (diagonal scale).   2.1 A középső elem (0,3 pont) A két optikai tengely a feketedoboz közepén metszi egymást. A metszéspontban lehet: egy teljesen fényvisszaverő tükör (mindkét oldalon), egy féligáteresztő tükör vagy egy szabályos háromszög alakú prizma, esetleg nincs ott semmi. Határozd meg, melyik elem helyezkedik el a feketedoboz közepén! Add meg az optikai nyílásokhoz ($A$, $B$, $C$ és $D$) képesti elhelyezkedését ‐ például egy vázlatos ábrával. Választásodat indokold.     2. ábra. A feketedoboz elrendezése és az ismeretlen elemek helyei     2.2 A többi helyen lévő elemek (2,2 pont) Az $A$, $B$, $C$, $D$ nyílások mögötti négy helyen az 1. táblázatban felsorolt elemek közül külön-külön van egy. Határozd meg az egyes helyeken lévő elemek típusát! Választásaidat indokold.   2.3 Tulajdonságok (7,5 pont) A Táblázatban egy második oszlop is található, ami a lehetséges elemeket jellemző tulajdonságokat tartalmazza. Határozd meg ezeket a jellemző tulajdonságokat azokra az optikai elemekre, amelyek a feketedoboz $A$, $B$, $C$ és $D$ helyein vannak olyan pontosan, amennyire lehetséges!   Táblázat. Lehetséges elemek a feketedobozban   ${\displaystyle \begin{array}{|cc|}\hline {\displaystyle \text{nincs elem }}\hfill & {\displaystyle \text{ csak levegő van ezen a helyen}}\hfill \\ {\displaystyle \text{tükör }}\hfill & {\displaystyle \text{ a tükör tengelye és az egyik optikai tengely közötti szög}}\hfill \\ {\displaystyle \text{prizma }}\hfill & {\displaystyle \text{ a prizma egyik oldala és a feketedoboz egyik optikai tengelye közötti szög, az alakja szabályos háromszög}}\hfill \\ {\displaystyle \text{gyűjtő- vagy szórólencse <br><span style="font-style: italic;">Megjegyzés:</span> A lencsék tengelyei mindig az optikai tengelyek mentén helyezkednek el.}}\hfill & {\displaystyle \text{ doboz közepétől mért távolság, fókusztávolságának nagysága és előjele}}\hfill \\ {\displaystyle \text{polarizátor }}\hfill & {\displaystyle \text{ a feketedoboz függőleges tengelyéhez képesti polarizáció szöge}}\hfill \\ {\displaystyle \text{egyetlen keskeny rés }}\hfill & {\displaystyle \text{ a doboz közepétől mért távolság, rés szélessége}}\hfill \\ {\displaystyle \text{optikai rács }}\hfill & {\displaystyle \text{ a doboz közepétől mért távolság, a csíkok iránya, a csíkok távolsága}}\hfill \\ {\displaystyle \text{tűlyuk }}\hfill & {\displaystyle \text{ a doboz közepétől mért távolság, lyukátmérő}}\hfill \\ \hline\end{array}}$   Fontos útmutatások: $•$ A lézer hullámhossza 650 nm. $•$ Tegyük fel, hogy az átlátszó elem törésmutatója 1,5.   Képek a mérési elrendezésről és az eszközökről     3. ábra. Mérési összeállítás és eszközök az 1. kísérleti feladathoz         4. ábra. A 2. kísérleti feladat eszközei. Megjegyzés: A lézeregységet a ragasztószalaggal rögzítheted az asztalhoz ‐ lásd a B-t.     Elméleti feladatok 1. Termikus lencsék (10 pont) Ha egy féligáteresztő lapra erős lézersugár esik, lehetséges, hogy az anyag inhomogén melegedése miatt az áthaladó fény önmagától fókuszálódik (self-focus) egy pontra a lemez mögött. Ez a jelenség (thermal lensing) olyan anyagokban figyelhető meg, amelyek törésmutatója a hőmérséklet növekedésével növekszik, amit egy pozitív $\gamma =\frac{\text{d}n}{\text{d}T}$ termo-optikai együttható jellemez. Egy $a=15\mathrm{,}0\text{mm}$ sugarú, $b=0\mathrm{,}2\text{mm}$ vastagságú és $A=0\mathrm{,}1$ optikai abszorpciós együtthatójú, féligáteresztő korong olyan anyagból készült, melynek hővezetési együtthatója $k=0\mathrm{,}3\text{W<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>K</mi></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math>}$ és termo-optikai együtthatója $\gamma =2\mathrm{,}5\cdot {10}^{-4}\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>K</mi></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math>}$. A korong külső pereme termikusan csatlakozik egy kör alakú fémtartóhoz (az ábrán nincs feltüntetve), amely a peremen 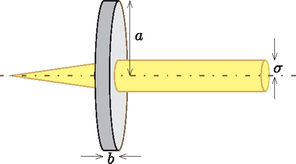    5. ábra     konstans $T_{\text{h}}=20{}^{\circ }$C hőmérsékletet biztosít. Egy párhuzamos, $\sigma =0\mathrm{,}5$ mm sugarú és $P_{\text{L}}=20$ mW teljesítményű lézersugár merőlegesen esik a korong közepére. Az intenzitáseloszlás a sugár teljes keresztmetszetén homogén. $a)$ Készíts egy kvalitatív grafikont a $T\left(r\right)$ hőmérséklet-eloszlásról, ahol $r$ a nyaláb tengelyétől mért távolság! A grafikonon egyértelműen jelöld be a $0\le r\le \sigma$ megvilágított és a $\sigma \le r\le a$ külső tartományt. (2 pont) $b)$ A korong középpontjának környezetében a hőmérséklet-eloszlást egy $T\left(r\right)=T_{\text{c}}+m{r}^2$ alakú másodfokú függvénnyel lehet leírni. Határozd meg a $T_{\text{c}}$ és $m$ paramétereket! (4 pont) $c)$ Mutasd meg, hogy a nyaláb valóban egy pontba fókuszálódik, és határozd meg ennek a pontnak a korongtól mért $f$ távolságát! Ha a $b)$ részben nem sikerült meghatároznod $T_{\text{c}}$ és $m$ értékét, használhatod őket paraméterként ebben a részben. (4 pont) Ne vedd figyelembe a korong hőtágulását. A hősugárzást, valamint a korong és a környező levegő közötti hőcserét hanyagold el. A környező levegő törésmutatója legyen $n=1$.   2. Tégla két sík között (10 pont) Egy kis méretű tégla két, párhuzamos sík közé van beszorítva a súlytalanság állapotában. A síkok merőlegesek a $z$ tengelyre. Az alsó sík az $x$ tengely irányába mozog állandó $u_1$ sebességgel, míg a felső az $y$ tengely irányába állandó $u_2$ sebességgel (lásd a 6. ábrát). A tégla kezdetben nyugalomban van. A tégla és az egyes síkok közötti csúszási súrlódási együttható megegyezik. $a)$ Határozd meg a tégla hosszú idő után kialakuló $v_{\infty }$ sebességét, ha $u_1=u_2$ (4 pont) $b)$ Határozd meg a tégla hosszú idő után kialakuló $v_{\infty }$ sebességét, ha $u_1\ne u_2$! (6 pont)     6. ábra         7. ábra.     3. Lemez mágnesek között (10 pont) Két, egyforma hosszúságú, hengeres, $R$ sugarú rúdmágnes közel van egymáshoz, és a függőleges szimmetriatengelyeik egybeesnek. A mágnesek polaritása megegyezik. Emiatt a mágnesek közötti légrésben a mágneses mező iránya a $+z$ tengely irányába mutat (lásd a 7. ábrát), és homogén $B$ indukcióval jellemezhető. A légrésen kívül nincs mágneses tér. A légrésbe egy nagy kiterjedésű, vízszintes, nem-mágneses fémlemezt helyezünk, és állandó $v$ sebességgel mozgatjuk vízszintesen a $+y$ tengely irányába. A fémlemez vastagsága $\delta$, a fajlagos ellenállása $\varrho$. $a)$ Vázold fel az áramvonalak alakját a fémlemezben egy adott időpillanatban! Tüntesd fel a tengelyeket a rajzon. (3 pont) $b)$ Határozd meg és ábrázold a fémlemezbeli áramsűrűséget a mágnesek szimmetriatengelyét metsző, az $y$ tengellyel párhuzamos egyenes mentén! (5 pont) $c)$ Mekkora vízszintes irányú erő szükséges a lemez mozgatásához? (2 pont)     ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Szász Krisztián, Vankó Péter</span>}}\hfill \end{array}}$