Cím: Hol él a kvantumbit? Utazás a dimenziók között
Szerző(k):  Pintér Gergő, Budapest 
Füzet: 2023/április, 196 - 202. oldal  PDF  |  MathML 
Témakör(ök): Matematika, Szakmai cikkek, Komplex számok trigonometrikus alakja, Koordináta-geometria, Vetítések, Modern fizika

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A számítástechnikában az információ alapegysége a bit, értéke 0 vagy 1 lehet, igen vagy nem. Technikailag a bit általában egy áramkör, amin vagy átfolyik az áram, vagy nem, ez jelzi a két állapotot. A digitális rendszerek minden adathalmazt 0-kból és 1-esekből álló jelsorozatokra, vagyis voltaképpen kettes számrendszerbeli számokra fordítanak le a szövegektől a videókig. A számítógépek a bitek nyelvét beszélik.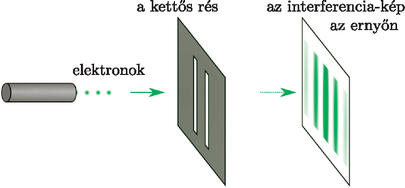
A kvantumszámítógépekben a bitek megfelelői a kvantumbitek (qubitek). Bár a gyakorlati megvalósításuk még gyerekcipőben jár, a kvantumbitek működése, a kvantumszámítógép programozása elméletben már egészen kidolgozott, izgalmas terület. A kvantumbiteknek is két értékük van, de csak akkor, ha megmérjük. Addig, amíg nem történik mérés, a kvantumbit egyszerre igen és nem, értéke egyszerre 0 és 1, de igazából egyik sem: az állapota valahol a két érték között ,,mozog'', úgynevezett szuperpozícióban van.
Jó asszociáció, ha erről Schrödinger macskája jut az eszünkbe. Maga Schrödinger, a kvantummechanika egyik kidolgozója az elmélet abszurditását próbálta érzékeltetni egy gondolatkísérlettel, amelyben egy dobozba zárt macska mellett egy fiolában mérges gáz van, és az állat egyszerre élő és halott, mert egy kvantumrendszer állapotától tesszük függővé a mérget tartalmazó fiola kinyílását. Eszerint a kérdés tehát az, hogy hogyan lehet egy macska egyszerre élő és halott, egy válasz egyszerre igen és nem, egy szám egyszerre 1 és 0.
A kvantumbit esetében ez a kérdés úgy szól, hogy milyen térben ,,mozog'' az állapota. Talán meglepő módon a kvantumbiteknek ezt a furcsa viselkedését egy geometriai konstrukcióval lehet jól leírni, ez a cikk erről a konstrukcióról szól. A geometriai alakzat, amit megmutatunk, a négydimenziós térben helyezkedik el, ami mindössze annyit jelent, hogy a pontoknak nem kettő vagy három, hanem négy koordinátájuk van. No meg azt, hogy nehezebb elképzelni őket, hogyan is néznek ki. De egy ügyes trükkel visszavetítve ezt a négydimenziós alakzatot a három dimenzióba lenyűgözően csavargó körvonalakként ábrázolhatjuk. Ezt hívják Hopf-fibrálásnak, Heinz Hopf német matematikusról elnevezve. A fibrálás meg nagyjából szálakra bontást jelent, mert ‐ mint ki fog derülni ‐ a kvantumbit állapotait mint egymás melletti vonalakból felépülő alakzatot képzelhetjük el.
Persze kérdés, hogy miért kell egy ilyen jelenséget mint a kvantumbit geometriailag leírnunk, mit segít ez például a kvantumszámítógépek vagy a szupravezetés megértésében. A válasz az, hogy a geometriai kép mindig segít, másfajta rálátást ad a problémára, ugyanúgy, mint egy ábra. Még akkor is, ha több dimenziós, mint ameddig a szemléletünk elér. Az igazi kérdés inkább az lehetne, hogy miért jó az emberiségnek a kvantumszámítógép és a szupravezetés. Ez a kérdés kikerülhetetlen, de nagyon messzire vezet. Ezt most nem részletezzük, de gondolkodnia mindenkinek érdemes rajta!
Minket tehát a geometriai kép érdekel, de mivel fizikai jelenségekről van szó, érdemes az egészet kontextusba helyezni. Aki már találkozott a most megemlítésre kerülő dolgokkal, rájuk ismerhet, és ha valakit jobban érdekelnek, az például az Az atomoktól a csillagokig* előadássorozat videóiban megtalálja mindegyiket.
A 20. század elején nem csak a művészetekben, de a tudományban is avantgarde irányzatok kaptak szárnyra. A képzeletünk határait súroló, álomszerű világképek léptek az addig egyeduralkodó newtoni ,,biliárdgolyó-valóság'' helyébe. Albert Einstein relativitáselmélete szerint nagy sebességek esetén egészen másképpen viselkedik a tér és az idő, mint azt megszoktuk [1].* A relativitáselmélethez fűződik a tömeg és az energia kapcsolatát megfogalmazó E=m⋅c2 formula, vagy a gravitációt újraértelmező görbült téridő koncepciója. Ezekről a továbbiakban nem lesz szó, ugyanis minket most a másik akkoriban kialakuló fizikai irányzat érdekel inkább, a kvantummechanika. A nanométeres mérettartományokban működő, elemi részecskék világát magában foglaló elméletet többek között Werner Heisenberg, Erwin Schrödinger és Albert Einstein dolgozta ki a 20. század első felében.
A kvantummechanika legismertebb következtetése a hullám-részecske kettős természet. Kiderült, hogy a fény, amire addig főleg hullámként gondoltak, részecskeként is viselkedik, fotonokból áll. Mindeközben az anyagi részecskék, mint például az elektron, amire addig apró golyóbisként gondoltak, hullámtulajdonságokat is mutat. Például a kétréses kísérletben mindkét résen egyidejűleg átmegy, és az ernyőn hullámok interferenciájára emlékeztető mintázatot mutatnak a becsapódások helyei. A kvantummechanikai leírás ezért nem részecskékről, de nem is hullámokról szól, hanem úgynevezett hullámfüggvényekről. Ezek írják le az elmélet egy másik bizarr jellemzőjét, a részecskék és a történések véletlenszerűségét. Ha meg akarjuk tudni egy részecskének valamilyen tulajdonságát, például a helyét, nem előre meghatározott, hanem véletlenszerű választ kapunk a mérés során. Akkor ,,találja ki'' a részecske, hogy hol van, amikor megmérjük! Említsük még meg azt a jellegzetességet, amiről az egész elmélet a nevét kapta. A ,,kvantum'' adagocskát jelent, és arra utal, hogy olyan mennyiségekről, amiket bár addig folytonosan változtathatónak képzeltek, de kiderült, hogy csak bizonyos meghatározott értékeket vehetnek fel, csak kis kvantumonként változhatnak. Ilyen mennyiség például az energia. A foton voltaképp az energia adagocskája.

 

 
A kétréses kísérlet
 

De hogyan állnak össze ezek a jelenségek egy elméletté? Röviden arról van szó, hogy a kvantummechanika egy nagyobb térben írja le a jelenségeket, mint amit közvetlenül érzékelni, mérni tudunk.
Képzeljünk el egy tavat, amiben a gyerekek úszkálnak, és tanító néni a partról vigyáz rájuk. Ő nem érzékeli a tavat, nem látja a gyerekeket, de van a tóban néhány bója, azokat ‐ és csak azokat ‐ érzékeli. Ha elkiáltja magát, hogy hol vagy Pistike, akkor Pistike szétnéz, odaúszik egy véletlenszerűen kiválasztott bójához, és ott jelentkezik. A tanító néni pedig megállapítja, hogy Pistike az ötös bójánál van. Pedig nem ott volt, csak a tanító néni kérdése miatt úszott oda. A tó felel meg egy kvantumrendszer állapotainak, azaz a hullámfüggvényeknek, a bóják pedig egy mérés lehetséges kimeneteleinek, mi csupán ennyit érzékelünk a tóból.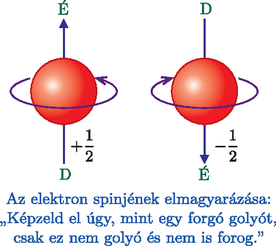
 
 


Egy kvantumbit önmagában egy rendszer. Olyan rendszer, aminek csak két bójája van, a mérés két lehetséges kimenetele. A kérdés tehát, hogy milyennek képzelhetjük el azt a tavat, amelyben csak két bója van. Ezek a legegyszerűbb kvantumrendszerek, a legkisebb tavak. De hol vannak ilyen kvantumbitek? A kvantumbit az információ egysége, ez fizikailag többféleképpen is megvalósulhat. A legismertebb az elemi részecskék spinje, ami egy adott irányban mérve állhat felfelé vagy lefelé. Hogy mi is az a spin, azt ‐ mint a mém is utal rá ‐ nem könnyű elképzelni.
A spint történeti okokból forgástengelynek szokták képzelni, de ez a kép nem is pontos, és félrevezető is lenne számunkra a továbbiakban [1].
A 2022-es fizikai Nobel-díjat a kvantumos összefonódással kapcsolatos kísérletekért adták. Ha két részecske összefonódott állapotban van, akkor egyiküknek sem határozott a spinje, de ha az egyikét megmérjük, akkor onnantól már a másiknál csak egyféle spint lehet mérni. Akkor is ezt tapasztaljuk, ha nagyon messze van egymástól a két részecske. De a spinen kívül van sok más kvantumbit is, például a kétréses kísérlet, ahol az a két állapot, hogy melyik résen megy keresztül a részecske. Ugyancsak egy kvantumbit információt hordoznak azok a szupravezető áramkörök is, amikben mindkét irányban egyszerre megy áram, de ha megmérjük, akkor véletlenszerűen beáll az egyik irányba.
Első megközelítésben a kvantumbit egy még le nem esett pénzérme. Minden pillanatban tartozik hozzá egy valószínűség, hogy ha épp most érné el a talajt, mennyi lenne a fej valószínűsége (pl. 30%, azaz 0,3), és persze ez már meghatározza az írásét is (pl. 70%, azaz 0,7). Ha ez csak ennyi lenne, akkor azt mondanánk, hogy a kvantumbit állapota egy szakaszon ,,él'', a [0,1] intervallumon, hiszen a valószínűség egy 0 és 1 közötti szám. De a teljes kvantummechanikai állapot ennél gazdagabb, annak csak egy vetülete ez a valószínűség. A teljes állapotot ‐ jelöljük Ψ-vel ‐ két síkbeli vektor (u és v) jellemzi, ezeket két óramutatóként is elképzelhetjük.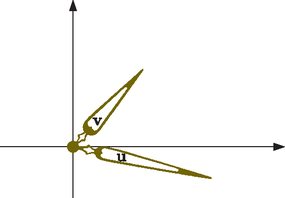
 
 

Ám ezek furcsa mutatók, mert nem csak tekergetni lehet őket, méghozzá egymástól függetlenül, de a hosszaik is állíthatóak. Az u vektor hosszának a négyzete az igen-nek (az 1-nek), a v hosszának a négyzete a nem-nek (a 0-nak) a valószínűsége. De az állapothoz hozzátartozik a két vektor iránya is. Mindkét vektort tudjuk forgatni és nyújtani, de ha az egyiket nyújtjuk, a másik megrövidül.
Milyen térben mozog tehát a kvantumbit, vagyis mi azon pontok halmaza, amikben előfordulhat? (Megmérni persze továbbra is csak a már említett két ,,bójánál'' tudjuk, az 1 vagy a 0 állapotban.) Egy koordináta-rendszerben a két helyvektor végpontjai u=(x,y) és v=(z,w). Vagyis egy konkrét Ψ állapotot ezzel a 4 koordinátával ‐ x, y, z és w ‐ jellemezhetünk, tehát az állapot a négydimenziós tér egy pontja. De hogyan képzeljünk el egy négydimenziós teret? Erre nagyon sok lehetséges válasz van [1], de most számunkra a legpraktikusabb, ha úgy gondolunk rá, mint két síkbeli mutató összes lehetséges állására, amit persze térként elképzelni nem is olyan egyszerű.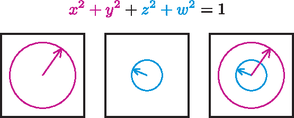
 
 


Azonban a mutatóknak nem minden állása megengedett, ugyanis az igen és a nem valószínűsége összesen 1 kell, hogy legyen. Tehát
|u|2+|v|2=1,
de tekintve, hogy a Pitagorasz-tétel szerint |u|2=x2+y2 és |v|2=z2+w2, azt kapjuk, hogy az x2+y2+z2+w2=1 egyenlőségnek kell teljesülnie.
Mit jelent ez? Miképpen a síkon x2+y2=1 egy origó középpontú 1 sugarú kör egyenlete ‐ hiszen azt fejezi ki, hogy az (x,y) pont az origótól 1 távolságra van ‐, a térben x2+y2+z2=1 az origó középpontú 1 sugarú gömbfelület egyenlete, x2+y2+z2+w2=1 a négy dimenziós térbeli ‐ szintén origó középpontú és 1 sugarú ‐ gömb egyenlete, vagyis azt fejezi ki, hogy az (x,y,z,w) pont az origótól 1 távolságra van.
Az a tó tehát, amelyben egy kvantumbit ψ állapota mozoghat, egy négydimenziós térbeli gömbfelület. A gömbök családja a körvonallal kezdődik, ez egydimenziós (1D gömb) és a háromdimenziós térbeli gömbfelülettel folytatódik, ami mint felület, kétdimenziós (2D gömb). A család következő tagja a négydimenziós térbeli gömbfelület, ő maga háromdimenziós (3D gömb) [1].
De van még egy csavar ‐ a szó szoros értelmében is ‐ a dologban! Ugyanis a fizikai tulajdonságok szempontjából csak a két mutató hosszúsága számít (ugye ezek határozzák meg a valószínűségeket) és az általuk bezárt szög. Azaz ha a két vektort egyszerre elforgatjuk ugyanazzal a szöggel, az fizikailag érdemben nem különböző eset. Mi lehet akkor a fizikailag releváns állapotok tere? Az összes lehetséges hossz a hozzájuk tartozó összes lehetséges közbezárt szöggel.
Egy konkrét állapot esetén fix az u és a v hossza, meg az általuk bezárt szög is. Még nem rögzített viszont ennek az egész rendszernek a helyzete a síkon. Minden állapotot el tudunk forgatni úgy, hogy az u mutató az x ‐ y síkon az x tengely pozitív irányába mutasson, és ilyenkor a fizikai állapotot meghatározza a v mutató állása ‐ hiszen az u hosszúságát meghatározza v hosszúsága, az irányát meg lefixáltuk. A v mutató az egységsugarú körlap bármelyik pontjába mutathat, tehát azt mondhatnánk, hogy a fizikailag releváns állapotok tere egy körlap. De vegyük észre, hogy ha a v hosszúsága 1, vagyis a körlap peremére mutat, akkor az u összemegy nullvektorrá.
 
 


Ilyenkor a két mutató egyszerre forgatásával igazából a v forog a körvonalon, ezek tehát fizikailag ugyanazt az állapotot jelölik, ez az állapot az egyik bója, a nem, hiszen az igen valószínűsége ilyenkor 0. Tehát a fizikailag releváns állapotok tere egy körlap, aminek a peremköre egyetlen pontnak számít. Olyan, mintha egy körlap alakú batyu peremét összehúznánk egy ponttá. Mit kapunk? Egy 2D gömbfelületet. Ezt talán könnyebb elképzelni, ha rátekintünk az ábrán levő térképre, amin a körlap teljes peremköre egyetlen pontot jelöl, a déli sarkot.
 
Tehát míg az összes állapotok tere a 3D gömbfelület, a fizikailag érdemben különböző állapotok tere a hagyományos 2D gömbfelület. A fizikusok ezt hívják Bloch-gömbnek. A két bója, az igen (v=(0,0)) és a nem (u=(0,0)), a gömbfelület két pólusa, erre utal az, hogy fel- vagy lefelé áll a spin. A köztük lévő szélességi körök egy-egy konkrét valószínűségnek felelnek meg, például az egyenlítő pontjaiban az igen és a nem valószínűsége egyaránt 50%.
 

Ha valaki jóban van a komplex számokkal ...
... annak ezt az egészet sokkal tömörebben is el lehet mondani. A mutatók az u=x+yi és v=z+wi komplex számok, maga az állapot pedig egy kétdimenziós komplex vektor:
Ψ=(u,v).
A fizikusok szeretik a két bázisvektort ‐ a bójákat ‐ így jelölni:
|1〉=(1,0)és|0〉=(0,1),
és így az állapot
Ψ=u|0〉+v|1〉.
Vagyis az állapot a kvantumbit 0 és 1 értékeinek szuperpozíciója, azaz komplex együtthatós lineáris kombinációja. Több állapotú rendszer esetén ugyanez történik, a mérhető állapotok szuperpozíciójaként egy megfelelő dimenziós komplex vektort kapunk.
A Bloch-gömbön a megfelelő pontot úgy kapjuk meg, ha az u és v komplex számokat átírjuk trigonometrikus alakba: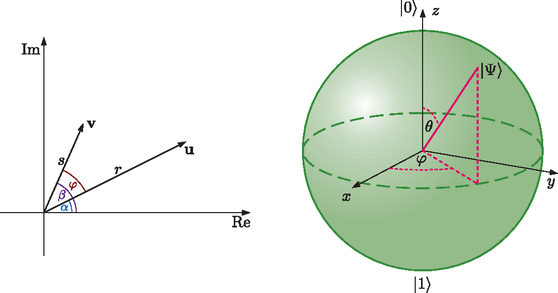
u=r(cosα+i⋅sinα)ésv=s(cosβ+i⋅sinβ),
majd a szögek különbségére bevezetjük a φ=β-α jelölést. Mivel r és s pozitív és r2+s2=1, ezért van olyan δ szög, amire α≤δ≤π/2 és r=cosδ és s=sinδ. Ekkor a Ψ állapothoz hozzárendelhetjük a gömbfelületnek azt a pontját, aminek φ a hosszúsági koordinátája, amelyre így teljesül, hogy 0≤φ≤2π, és θ=2δ a szélességi koordinátája, amire pedig a 0≤θ≤π egyenlőtlenség teljesül.
 

 
A két komplex szám szöge és hossza, és a Bloch-gömb koordinátái
 

Feladat: Ellenőrizzük, hogy így valóban egy jóldefiniált pontot adtunk meg a körvonalon, ami csak a Ψ-hez tartozó fizikailag releváns állapottól függ. Mutassuk meg, hogy ez ugyanaz a konstrukció, mint az u mutató beforgatása, majd a batyu peremének összehúzása.
 

A két mutató együttes körbeforgatása által minden fizikailag különböző állapothoz körvonalnyi sok tényleges állapot tartozik. Geometriailag ez azt jelenti, hogy a 2D gömbfelület minden pontjához tartozik egy körvonal a 3D gömbfelületen, és ezek a körök kitöltik a 3D gömbfelületet, azaz minden pont pontosan egy ilyen körön van rajta. Ezt nevezik Hopf-fibrálásnak: a 3D gömbfelület 2D gömbfelületnyi sok 1D gömbfelület ‐ azaz körvonal ‐ uniója. (Ezeket a köröket nevezik Hopf-köröknek.) Ezt persze nagyon nem könnyű elképzelni. Vajon meg tudjuk jeleníteni valahogy ezeket a köröket?
Elég reménytelennek tűnik, de meg lehet csinálni! A sztereografikus projekció segítségével egy 2D gömbfelületet egy pontjából ki tudjuk vetíteni a gömböt az átellenes pontjában érintő síkra, ahogy az ábra mutatja.
 

 
A sztereografikus projekció
 
 

Egyedül a vetítési pontnak nem lesz képe, vagy ha úgy tetszik, a végtelenbe vetül. Ugyanezen a módon a 3D gömbfelületet kivetíthetjük a háromdimenziós térbe egyik pontjából. Ezáltal a Hopf-körök képei egymással hurkolódó körök lesznek, a körök mindegyike egy-egy fizikailag releváns állapotot jelenít meg. A középső vízszintes kör az egyik bója (például az igen), a középpontján átmenő merőleges egyenes pedig a másik bója (a nem). A többiek egyre dagadtabb tóruszfelületeken ferdén futó körök, egyszer megkerülik a tóruszt a meridián irányban (megkerülik a tórusz csövét), és longitúdó irányban is (a tórusz középköre mentén körbe). Az egyre dagadtabb tóruszok felelnek meg a Bloch-gömb szélességi köreinek, tehát a konkrét valószínűségeknek.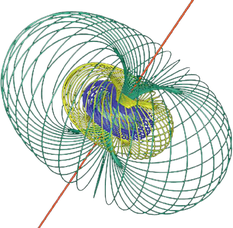
 
 
Hopf-fibrálás a térben
 

Ahogy a szélességi kör rászűkül a gömb egyik pólusára, a hozzá tartozó tórusz az igen-körré húzódik össze, a másik pólusnál pedig a végtelen méretűvé dagadó tórusz a nem egyenesére húzódik rá. Persze a 3D gömbben az összes Hopf-kör ugyanakkora méretű, és a nem egyenese is egy ugyanilyen kör, csak a térben a vetítés miatt különböző méretűek lettek, ahogy az árnyékok is megnyúlnak.
Összefoglalva, egy kvantumbit állapotait a Hopf-fibrálás szemléltetheti. A teljes állapotok a négydimenziós térbeli 3D gömbfelület pontjai, a fizikailag releváns állapotok a háromdimenziós térbeli 2D gömbfelület pontjai. A 2D gömbfelület minden pontjához tartozik egy kör a 3D gömbfelületen, ezen helyezkednek el az azonos fizikailag releváns állapotok.
Ezek a körök alkotják a Hopf-fibrálást, ami a sztereografikus projekció segítségével a háromdimenziós térben is megjeleníthető. Niles Johnson animációján jól követhetőek ezek a körök: https://youtu.be/AKotMPGFJYk.
 
Irodalom


[1]Pintér Gergő: Új világok teremtése ‐ Geometriai képzetek és képződmények, Typotex Kiadó (2020).

*http://atomcsill.elte.hu/NEW/

*A szerző Új világok teremtése című könyvében a témáról bővebben is olvashatunk.