Cím:	Megoldásvázlatok a 2022/9. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Kozma Katalin Abigél, Győr ,  Számadó László, Budapest
Füzet:	2023/január, 13 - 22. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Az $a_n$ számtani sorozat különbsége $4$, az első hét tagjának összege $105$. Adjuk meg a sorozat első tagját. (3 pont) $b)$ A $b_n$ mértani sorozat hányadosa $4$, az első hét tagjának összege $16383$. Adjuk meg a sorozat első tagját. (3 pont) $c)$ A $c_n$ sorozat minden tagja az $n$ elsőfokú függvénye. A sorozat második tagja $7$, a hetedik tagja $27$. Adjuk meg a sorozat első tagját. (5 pont)   Megoldás. $a)$ A szokásos jelölésekkel: $a_1+\left(a_1+4\right)+\left(a_1+8\right)+\left(a_1+12\right)+\left(a_1+16\right)+\left(a_1+20\right)+\left(a_1+24\right)=105$, amelyből ${7a}_1+84=105$, $a_1=3$. $b)$ A mértani sorozat összegképlete alapján:   $b_1\cdot \frac{q^n-1}{q-1}=16383$, behelyettesítés után $b_1\cdot \frac{4^7-1}{4-1}=16383$, amelyből megkapjuk, hogy $b_1=3$. $c)$ A feltételek alapján: $c_n=a\cdot n+b$, ahol $a$, $b$ valós számok, de $a\ne 0$. Továbbá, $c_2=a\cdot 2+b=7$ és $c_7=a\cdot 7+b=27$, így a következő egyenletrendszert kapjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2a+b}& {\displaystyle =\mathrm{7,}}\hfill \\ \hfill {\displaystyle 7a+b}& {\displaystyle =27.}\hfill \end{array}}$ Az egyenletrendszer megoldása: $a=4$, illetve $b=-1$, amelyből $c_1=4\cdot 1-1=3.$   2. $a)$ Oldjuk meg az alábbi egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle 5^{-x+1}-10\cdot 5^{-x-1}+6\cdot 5^{-x-2}=16\mathrm{,}2.}\end{array}$ (6 pont) $b)$ Igazoljuk, hogy $\begin{array}{c}{\displaystyle \text{lg}{3}^{2x}\cdot \text{lg}{7}^{2x}\le {\left(\text{lg}{3}^x+\text{lg}{7}^x\right)}^2}\end{array}$ minden valós $x$ esetén fennáll. (7 pont)   Megoldás. $a)$ A hatványozás azonosságait használva: $\begin{array}{c}{\displaystyle {5\cdot 5}^{-x}-2\cdot 5^{-x}+0\mathrm{,}24\cdot 5^{-x}=16\mathrm{,}\mathrm{2,}}\end{array}$ amelyből ${3\mathrm{,}24\cdot 5}^{-x}=16\mathrm{,}2$, ezért $5^{-x}=5^1$. Az $5$-ös alapú exponenciális függvény kölcsönösen egyértelmű, ezért $x=-1$. Ellenőrzés behelyettesítéssel vagy hivatkozás az ekvivalens átalakításokra. $b)$ A bizonyítandó állításban szereplő kifejezések minden valós $x$-re értelmezettek. Rendezzük $0$-ra, és hajtsunk végre néhány ekvivalens átalakítást: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0}& {\displaystyle \le {\left({\text{lg}3}^x+{\text{lg}7}^x\right)}^2-{\text{lg}3}^{2x}\cdot {\text{lg}7}^{2x}={\left({\text{lg}3}^x+{\text{lg}7}^x\right)}^2-\text{lg}{\left(3^x\right)}^2\cdot \text{lg}{\left(7^x\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle \le {\left({\text{lg}3}^x+{\text{lg}7}^x\right)}^2-4\cdot {\text{lg}3}^x\cdot {\text{lg}7}^x\mathrm{,}\text{amelyből}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle \le {\left({\text{lg}3}^x-{\text{lg}7}^x\right)}^2\mathrm{.}}\hfill \end{array}}$ A kapott egyenlőtlenség igaz, és ezzel állításunkat igazoltuk.   3. Egy üzemben $5$ milliméter vastagságú, $80$ centiméter oldalhosszúságú négyzet alakú acéllapokból a lehető legnagyobb, szabályos tizenkétszögeket vágnak ki úgy, hogy a tizenkétszögek két-két oldala illeszkedjen a négyzetlapok oldalára. Tudjuk, hogy az acél sűrűsége $7\mathrm{,}8\frac{\text{g}}{{\text{cm}}^3}$. $a)$ Mekkora lesz $75$ darab legyártott tizenkétszög tömege? (7 pont) A szabályos tizenkétszög csúcsait megszámozzuk sorban $1$-től $12$-ig. A sorszámozott csúcsok közül bármelyik három egy-egy háromszöget alkot. $b)$ Adjuk meg az így kapott derékszögű és nem derékszögű háromszögek számát. 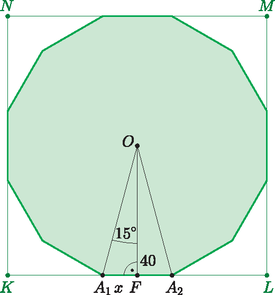(6 pont)   Megoldás. $a)$ Legyen a kiinduló négyzet a $KLMN$, és a tizenkétszög $A_1{A}_2$ oldala illeszkedjen a négyzet $KL$ oldalára. Legyen továbbá a négyzet átlóinak metszéspontja $O$, a $KL$ felezőpontja pedig $F$.     Használjuk az ábra jelöléseit. A szabályos tizenkétszög tulajdonságai és a megadott adatok alapján: $A_{1}O{A}_2\sphericalangle ={30}^{\circ }$, $OF=40$ cm, vagyis $A_{1}OF\sphericalangle ={15}^{\circ }$. Az $A_{1}OF$ derékszögű háromszögből kapjuk, hogy $x=40\cdot \text{tg}{15}^{\circ }$. A tizenkétszög területe (${\text{cm}}^2$-ben): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle =12\cdot T_{A_1{A}_{2}O}=12\cdot \frac{A_1{A}_2\cdot OF}{2}=12\cdot x\cdot OF=12\cdot \left(40\cdot \text{tg}{15}^{\circ }\right)\cdot 40=19200\cdot \text{tg}{15}^{\circ }\mathrm{.}}\hfill \end{array}}$ A megadott sűrűséggel a $75$ darab, $0\mathrm{,}5$ centiméter vastagságú tizenkétszög tömege $\begin{array}{c}{\displaystyle 75\cdot 19200\cdot \text{tg}{15}^{\circ }\cdot 0\mathrm{,}5\cdot 7\mathrm{,}8\approx 1504803\left(\text{gramm}\right)\mathrm{,}}\end{array}$ amely kerekítve $1505$ kilogramm. $b)$ A Thalész-tétel (megfordítása) miatt derékszögű háromszöget akkor kapunk, ha a háromszög leghosszabb oldala a tizenkétszög köré írt körének átmérője, tehát ennek az oldalnak a két végpontja a tizenkétszög két átellenes csúcsa. Ilyen módon két csúcsot hatféleképpen tudunk választani: $A_1{A}_7$, $A_2{A}_8$, $A_3{A}_9$, $A_4{A}_{10}$, $A_5{A}_{11}$, $A_6{A}_{12}$. A háromszög harmadik, a derékszögű csúcsa a maradék 10 csúcs közül bármelyik lehet. Ez mind a hat esetben $10$ lehetőséget jelent, vagyis a derékszögű háromszögek száma: $6\cdot 10=60$. Az összes háromszög számát úgy kapjuk, ha a $12$ csúcs közül az összes lehetséges módon kiválasztunk három darabot. Ezeknek a száma: $\left(\genfrac{}{}{0ex}{}{12}{3}\right)=\mathrm{220,}$ azaz a nem derékszögű háromszögek száma: $220-60=160$.   4. Magyarországon $2022$-ig a gépkocsik (nem egyedi) rendszáma három betűből és három számjegyből állt. Az ábécé $26$ betűje használható ezekben a rendszámokban. $a)$ Hány autó kaphat ilyen módon rendszámot? (4 pont) $b)$ Hány olyan rendszám lehet, amelyikben kétféle betű, és kétféle számjegy szerepel? (5 pont) $c)$ Az elképzelhető összes rendszámból véletlenszerűen választunk egy darabot. Mekkora a valószínűsége annak, hogy három különböző betűből és három különböző számjegyből áll ez a rendszám? (5 pont)   Megoldás. $a)$ Mivel többször is szerepelhetnek a betűk és a számjegyek is egy-egy rendszámban, ezért a három betű ${26}^3$, a három számjegy pedig ${10}^3$ darab lehet, az összes lehetőség ezek alapján: ${26}^3\cdot {10}^3=17576000$. $b)$ Legyen a rendszámban szereplő kétféle betű az A és a B. Ezek $6$-féleképpen fordulhatnak elő: AAB, ABA, BAA, ABB, BAB, BBA. Mivel a $26$ betű közül $\left(\genfrac{}{}{0ex}{}{26}{2}\right)$-féleképpen választhatunk ki két betűt, ezért minden választás esetén $6\cdot \left(\genfrac{}{}{0ex}{}{26}{2}\right)$, azaz $1950$ rendszám betűit tudjuk előállítani. A számjegyek esetén is hasonlóan gondolkodhatunk: $6\cdot \left(\genfrac{}{}{0ex}{}{10}{2}\right)=270$. Ezek alapján az összes megfelelő rendszám darabszáma: $1950\cdot 270=526500$. $c)$ Az összes elképzelhető rendszám száma: ${26}^3\cdot {10}^3$. Mivel most csak egyszer szerepelhetnek a betűk és a számjegyek is egy-egy rendszámban, ezért a három betű $26\cdot 25\cdot 24$, a három számjegy pedig $10\cdot 9\cdot 8$ darab lehet. A kedvező lehetőségek száma ezek alapján: $26\cdot 25\cdot 24\cdot 10\cdot 9\cdot 8$. A keresett valószínűséget a kedvező esetek számának és az összes eset számának hányadosa adja, vagyis annak a valószínűsége, hogy a kiválasztott rendszám három különböző betűből és három különböző számjegyből fog állni: $\begin{array}{c}{\displaystyle p=\frac{26\cdot 25\cdot 24\cdot 10\cdot 9\cdot 8}{{26}^3\cdot {10}^3}=\frac{25\cdot 24\cdot 9\cdot 8}{{26}^2\cdot {10}^2}\approx 0\mathrm{,}639.}\end{array}$   II. rész   5. Adott a következő két függvény: $\begin{array}{c}{\displaystyle f:\text{R}\to \text{R};f\left(x\right)=-x-\mathrm{1,}\text{és}g:\text{R}\to \text{R};g\left(x\right)=-x^2-10x-19.}\end{array}$ $a)$ Oldjuk meg az $f\left(x\right)=g\left(x\right)$ egyenletet a valós számok halmazán. (3 pont) $b)$ Írjuk fel az $y=f\left(x\right)$ és az $y=g\left(x\right)$ egyenletű alakzatok közös pontjaiban az $y=g\left(x\right)$ egyenletű görbéhez húzható érintők egyenletét. (7 pont) $c)$ Számítsuk ki az $y=f\left(x\right)$ és az $y=g\left(x\right)$ egyenletű alakzatok által közbezárt síkidom területét. (6 pont)   Megoldás. $a)$ Rendezés után a következő másodfokú egyenletet kell megoldanunk: $x^2+9x+18=0$. A másodfokú egyenlet megoldóképletének alkalmazásával látható, hogy $x_1=-3$, $x_2=-6$. $b)$ Adott pontban a függvénygrafikon érintőjének meredeksége egyenlő a függvény első deriváltjának értékével. Mivel $g\text{'}\left(x\right)=-2x-10$, ezért az $e_1$ érintő meredeksége $m_1=g\text{'}\left(-3\right)=-4$, az $e_2$ érintő meredeksége $m_2=g\text{'}\left(-6\right)=2.$ Az $e_1$ egyenes átmegy a $g\left(x\right)$ grafikonjának $P_1\left(-3;2\right)$ pontján, ezért $2=-4\cdot \left(-3\right)+b_1$, amelyből $b_1=-10$, így $e_1:y=-4x-10$. Hasonlóképpen, a $P_2\left(-6;5\right)$ pont illeszkedik az $e_2$ egyenesre, ezért $5=2\cdot \left(-6\right)+b_2$, ebből $b_2=17$, tehát $e_2:y=2x+17$. $c)$ A grafikonok által meghatározott síkidom területét a következő határozott integrál kiszámításával kaphatjuk meg: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\int }_{-6}^{-3}\left(g\left(x\right)-f\left(x\right)\right)\text{d}x}& {\displaystyle ={\int }_{-6}^{-3}\left(-x^2-9x-18\right)dx={\left[-\frac{x^3}{3}-4\mathrm{,}5x^2-18x\right]}_{-6}^{-3}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =22\mathrm{,}5-18=4\mathrm{,}5.}\hfill \end{array}}$ A síkidom területe $4\mathrm{,}5$ területegység.   6. 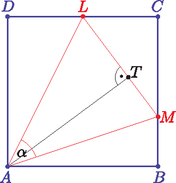Egy $600$ méter oldalhosszúságú, négyzet alakú parkot futópálya határol. A park egyik csúcsától indítja András, az edző a két futóatlétáját, akik egyszerre indulnak, de más irányban. András helyben marad, Lali $9\text{km/h}$, Máté $8\text{km/h}$ egyenletes sebességgel fut az edzésen. $6$ perc elteltével a három szereplő az $ALM$ háromszög csúcsaiban van, ahol a háromszög csúcsait a szereplők nevének a kezdőbetűjével jelöltük. $a)$ Milyen messze van ekkor Andrástól Lali és Máté? (4 pont) $b)$ Milyen messze van ekkor egymástól a két futó? (2 pont) $c)$ Igazoljuk, hogy ekkor András pontosan ${45}^{\circ }$-os szögben látja az $LM$ szakaszt. (5 pont) $d)$ A parkban az $L$ és $M$ között van egy egyenes sétaút is. Milyen messze van András ettől az úttól? (5 pont)   Megoldás. $a)$ $6$ perc, azaz $0\mathrm{,}1$ óra alatt Lali $900$ métert, Máté pedig $800$ métert fut. Ezek alapján: $AD+DL=600+300=900$ méter, $AB+BM=600+200=800$ méter. A Pitagorasz-tételt használva az $ADL$ derékszögű háromszögben András és Lali távolsága: ${AL}^2={AD}^2+{DL}^2={600}^2+{300}^2=450000$, amelyből $AL=\sqrt[]{450000}=300\sqrt[]{5}\approx 671$ méter.     A Pitagorasz-tételt használva az $ABM$ derékszögű háromszögben András és Máté távolsága: ${AM}^2={AB}^2+{BM}^2={600}^2+{200}^2=400000$, amely alapján $AM=\sqrt[]{400000}=200\sqrt[]{10}\approx 632$ méter. Andrástól Lali $671$ méterre, Máté pedig $632$ méterre van. $b)$ Mivel $DL=300$, ezért $LC=300$. Mivel $BM=200$, ezért $MC=400$. A Pitagorasz-tételt használva az $LCM$ derékszögű háromszögben Lali és Máté távolsága: $LM=\sqrt[]{{LC}^2+{MC}^2}=\sqrt[]{{300}^2+{400}^2}=500$ (méter). A két sportoló $500$ méterre van egymástól. $c)$ Az ALM háromszögre használjuk a koszinusztételt: $\begin{array}{c}{\displaystyle {LM}^2={AL}^2+{AM}^2-2\cdot AL\cdot AM\cdot \text{cos}\alpha \mathrm{.}}\end{array}$ A háromszög oldalainak hosszát már ismerjük, végezzük el a behelyettesítést, de az igazolás miatt csakis a pontos értékeket használhatjuk: $\begin{array}{c}{\displaystyle 250000=450000+400000-2\cdot 300\sqrt[]{5}\cdot 200\sqrt[]{10}\cdot \text{cos}\alpha \mathrm{,}}\end{array}$ amelyből azt kapjuk, hogy $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{450000+400000-250000}{2\cdot 300\sqrt[]{5}\cdot 200\sqrt[]{10}}=\frac{600000}{120000\cdot \sqrt[]{50}}=\frac{5}{5\sqrt[]{2}}=\frac{1}{\sqrt[]{2}}=\frac{\sqrt[]{2}}{2}\mathrm{.}}\end{array}$ Az $\alpha$ egy háromszög belső szöge, ezért a $\text{cos}\alpha =\frac{\sqrt[]{2}}{2}$ egyenlet megoldását a $\left]0^{\circ };{180}^{\circ }\right[$-on keressük. Az egyedüli megoldás $\alpha ={45}^{\circ }$, és ezzel az állítást igazoltuk. $d)$ Az $AT$ szakasz hosszát kell meghatároznunk. Írjuk fel az $ALM$ háromszög területét kétféleképpen: $\begin{array}{c}{\displaystyle T=\frac{LM\cdot AT}{2}=\frac{500\cdot AT}{2}=250\cdot AT\mathrm{,}}\end{array}$ illetve $\begin{array}{c}{\displaystyle T=\frac{AL\cdot AM\cdot \text{sin}\alpha }{2}=\frac{300\sqrt[]{5}\cdot 200\sqrt[]{10}\cdot \frac{\sqrt[]{2}}{2}}{2}=150000.}\end{array}$ Ebből következik, hogy $250\cdot AT=150000$, azaz $AT=600$ (m). András $600$ méterre van az úttól.   7. Boglárka érdekes számhármasokat gyűjtött, és a következőket állapította meg: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 3^2+4^2}& {\displaystyle =5^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 5^2+{12}^2}& {\displaystyle ={13}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 7^2+{24}^2}& {\displaystyle ={25}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 9^2+{40}^2}& {\displaystyle ={41}^2\mathrm{.}}\hfill \end{array}}$ $a)$ Béla meglátta Boglárka egyenleteit és elgondolkodott azon, hogy lehet-e egy ilyen tulajdonságú számhármas legkisebb eleme a $2023$. Segítsünk Bélának, határozzuk meg $k\in \text{Z}$ értékét, ha ${2023}^2+k^2={\left(k+1\right)}^2$. (4 pont) $b)$ Bálint azt állítja, hogy a végtelenségig folytatható az egyenlőségek sorozata, azaz minden $2n+1$ $\left(n\in \text{N}\right)$ alakú páratlan szám négyzetéhez hozzáadva a $2n\left(n+1\right)$ négyzetét, éppen a következő négyzetszámot kapjuk. Igazoljuk Bálint állítását. (6 pont) $c)$ Bizonyítsuk be, hogy $1^{2023}+2^{2023}+3^{2023}+4^{2023}+5^{2023}$ osztható $5$-tel. (6 pont)   Megoldás. $a)$ Bontsuk fel a zárójelet, majd az egyenlet mindkét oldalából vonjunk ki $k^2$-t: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {2023}^2+k^2}& {\displaystyle =k^2+2k+\mathrm{1,}}\hfill \\ \hfill {\displaystyle {2023}^2}& {\displaystyle =2k+1.}\hfill \end{array}}$ Ebből rendezés után azt kapjuk, hogy $\begin{array}{c}{\displaystyle k=\frac{{2023}^2-1}{2}=2046264.}\end{array}$ Ellenőrzés: ${2023}^2+2046{264}^2=4187200450225=2046{265}^2$. $b)$ Bálint állítása a következő: Minden $n\in \text{N}$-re igaz, hogy $\begin{array}{c}{\displaystyle {\left(2n+1\right)}^2+{\left(2n\left(n+1\right)\right)}^2={\left(2n\left(n+1\right)+1\right)}^2\mathrm{.}}\end{array}$ Az egyenlet bal oldalából kiindulva, azonos átalakításokat végzünk: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 4n^2+4n+1+4n^2\left(n^2+2n+1\right)=4n^2\left(n^2+2n+1\right)+4n\left(n+1\right)+1=}\hfill \\ \hfill {\displaystyle ={\left(2n\left(n+1\right)\right)}^2+2\cdot 2n\left(n+1\right)+1={\left(2n\left(n+1\right)+1\right)}^2\mathrm{,}}\hfill \end{array}}$ így éppen a jobb oldalon álló kifejezést kapjuk. Ezzel a bizonyítás végére értünk, megmutattuk, hogy Bálint állítása igaz. $c)$ I. megoldás. Az $1^{2023}=1$, a $2$ pozitív egész kitevőjű hatványainak végződései négyesével ismétlődnek ($\mathrm{2,4,8,6,2,}\text{...}$), és $2023=505\cdot 4+3$, ezért a $2^{2023}$ utolsó számjegye $8$. A $3$ pozitív egész kitevőjű hatványainak végződései is négyesével ismétlődnek ($\mathrm{3,9,7,1,3,}\text{...}$), ezért a $3^{2023}$ utolsó számjegye $7$. A $4$ pozitív egész kitevőjű hatványainak végződései kettesével ismétlődnek ($\mathrm{4,6,4,}\text{...}$), tehát páratlan kitevő esetén $4$-re végződnek, ezért a $4^{2023}$ utolsó számjegye $4$. Az $5$ pozitív egész kitevőjű hatványainak végződése mindig $5$, tehát az $5^{2023}$ utolsó jegye $5$. Ezek alapján az öttagú összeg utolsó jegye $5$, vagyis osztható $5$-tel. Ezzel a bizonyítás kész. II. megoldás. Mivel az $5$ bármelyik pozitív egész kitevőjű hatványa osztható $5$-tel, így elég megmutatnunk, hogy $1^{2023}+2^{2023}+3^{2023}+4^{2023}$ osztható $5$-tel. A kifejezés tagjait alkalmasan csoportosítjuk: $\begin{array}{c}{\displaystyle 1^{2023}+4^{2023}+2^{2023}+3^{2023}\mathrm{,}}\end{array}$ majd alkalmazzuk az $\begin{array}{c}{\displaystyle a^n+b^n=\left(a+b\right)\left(a^{n-1}-a^{n-2}b+a^{n-3}{b}^2\text{...}\pm \text{...}-a{b}^{n-2}+b^{n-1}\right)}\end{array}$ azonosságot, amelyben $n$ pozitív, páratlan szám: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \left(1^{2023}+4^{2023}\right)+\left(2^{2023}+3^{2023}\right)=}\hfill \\ \hfill {\displaystyle =\left(1+4\right)\cdot \text{(egész szám)}+\left(2+3\right)\cdot \text{(egész szám)}=5\cdot \text{(egész szám)}\mathrm{,}}\hfill \end{array}}$ azaz beláttuk, hogy a kifejezés osztható $5$-tel.   8. Egy vállalkozás olyan négyzet alapú egyenes gúlákat rendel reklámajándéktárgyként, amelyeknek az oldallapjai az alaplappal ${60}^{\circ }$-os szöget zárnak be, és az alapéleinek a hossza $12$ centiméter. A négy kiemelkedő termékük reklámját szeretnék elhelyezni a gúla egy-egy oldallapján. $a)$ Határozzuk meg mekkora területű részre kell megtervezni egy termék reklámját. (3 pont) $b)$ Mekkora a gúla térfogata? (3 pont) $c)$ Mekkora szöget zárnak be a gúla oldalélei az alaplappal? (4 pont) $d)$ A gúla alakú dobozok belsejében egy-egy (gömb alakú) ajándék labdát is elhelyeznek, amelyek mind a négy oldallapot és az alaplapot is érintik. Mekkora a labda sugara? 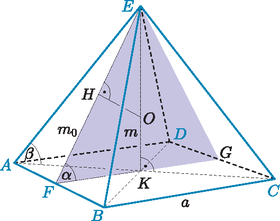(6 pont)   Megoldás. $a)$ Legyen az $AC$ és a $BD$ átló metszéspontja $K$, a gúla testmagassága $EK=m$. Az $AB$ él felezőpontja $F$, így $FE=m_0$ az $ABE$ oldallap magassága, és $KFE\sphericalangle =\alpha ={60}^{\circ }$ az alaplap és az oldallapok bezárt szöge. A $KFE$ derékszögű háromszögből $\begin{array}{c}{\displaystyle m_0=\frac{a}{2\cdot \text{cos}{60}^{\circ }}=\frac{12}{2\cdot \text{cos}{60}^{\circ }}=12\left(\text{cm}\right)\mathrm{.}}\end{array}$     Ezt felhasználva a gúla egy oldallapjának a területe, ahová egy terméknek a reklámját kell megtervezni: $\begin{array}{c}{\displaystyle T_{\text{oldallap}}=\frac{a\cdot m_0}{2}=\frac{12\cdot 12}{2}=72{\text{cm}}^2\mathrm{.}}\end{array}$ $b)$ A $KFE$ derékszögű háromszögből $\begin{array}{c}{\displaystyle m=\frac{a}{2}\cdot \text{tg}{60}^{\circ }=\frac{12}{2}\cdot \text{tg}{60}^{\circ }=6\cdot \sqrt[]{3}\text{cm}\mathrm{.}}\end{array}$ A gúla térfogata: $\begin{array}{c}{\displaystyle V=\frac{a^2\cdot m}{3}=\frac{{12}^2\cdot 6\cdot \sqrt[]{3}}{3}=288\cdot \sqrt[]{3}\approx 498\mathrm{,}8\left({\text{cm}}^3\right)\mathrm{.}}\end{array}$ $c)$ A gúla forgásszimmetrikus, ezért az oldalélek az alaplappal ugyanakkora szöget zárnak be. Az $EA$ oldalél alaplappal alkotott $\beta$ szögét az $EAK$ derékszögű háromszögből határozhatjuk meg: $\begin{array}{c}{\displaystyle \text{tg}\beta =\frac{EK}{KA}=\frac{\frac{\sqrt[]{3}}{2}\cdot 12}{\frac{\sqrt[]{2}}{2}\cdot 12}=\sqrt[]{\frac{3}{2}}\mathrm{,}}\end{array}$ innen $\beta \approx 50\mathrm{,}{77}^{\circ }$. $d)$ A gúla beírt gömbjének sugarát kell meghatároznunk. Ez a gömb az oldallapokat azok lapmagasságain, az alaplapot a négyzet átlóinak metszéspontjában érinti. Legyen a $CD$ él felezőpontja $G$, a gúlának egy alaplapra merőleges síkmetszete a $GFE$ háromszög. A beírt gömb $O$ középpontja az $EK$ tengelyre illeszkedik, ezért a $GFE$ sík egy olyan főkört metsz ki a gömbből, amely egyúttal a $GFE$ háromszög beírt köre. A $GFE$ háromszögben $FO$ szögfelező, ezért $OFK\sphericalangle ={30}^{\circ }$. A gömb sugara: $\begin{array}{c}{\displaystyle r=KO=KF\cdot \text{tg}{30}^{\circ }=6\cdot \frac{\sqrt[]{3}}{3}=2\cdot \sqrt[]{3}\approx 3\mathrm{,}5.}\end{array}$ A gúla alakú dobozokban $3\mathrm{,}5$ cm sugarú labdákat helyeztek el.   Megjegyzés. A $GFE$ háromszög beírt körének $r$ sugara többféleképpen is meghatározható. Alkalmazhattuk   volna az $r=\frac{t}{s}$ képletet, de hasonlósággal is célt lehetne érni. Ha a kör az $EF$ szakaszt $H$-ban érinti, akkor az $EHO$ és az $EKF$ háromszögek hasonlók.   9. $a)$ Egy matematikatanár tanít a 12. A és a 12. B osztályban is. Íratott egy közös dolgozatot, amelyben $120$ pont volt az elérhető legmagasabb pontszám. Az A osztályban $84$ pont, a B osztályban $74$ pont lett az átlag. Az A osztályos fiúk átlagosan $81$, a B osztályos fiúk pedig $71$ pontot értek el. Az A osztályban a lányok átlagosan $90$, míg a B osztályban a lányok átlagosan $76$ pontos dolgozatot írtak. Tudjuk továbbá, hogy az összes fiú átlaga $79$ pont lett. Mennyi a két osztályban az összes lány átlagpontszáma? (8 pont) $b)$ Az A osztályban tanuló Andrásnak hat jegye van matematikából, és a hat jegynek a mediánja $4$. Mit mondhatunk a B osztályban tanuló Benedek matematikajegyeinek mediánjáról, ha hat jegye pontosan megegyezik András jegyeivel, de neki van még ezen túl egy hetedik jegye, amely $5$-ös? (4 pont) $c)$ Három barátnő, Anna, Bea és Cili matematikából, fizikából és kémiából elért félévi eredményeiket vizsgálta. I. Kiszámolták mindegyiküknek az átlagát, majd ezeknek az átlagoknak vették az átlagát. II. Kiszámolták a három tantárgy átlagát, majd ezen átlagok átlagát vették. Mutassuk meg, hogy a kétféle módon kapott átlag egyenlő egymással. (4 pont)   Megoldás. $a)$ A következő táblázat tartalmazza az ismert átlagokat, az összes lány átlagpontszámát jelölje $x$:   ${\displaystyle \begin{array}{|cccc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{ fiúk átlaga }}\hfill & \hfill {\displaystyle \text{ lányok átlaga }}\hfill & \hfill {\displaystyle \text{ osztály átlaga }}\hfill \\ \hfill {\displaystyle \text{12. A }}\hfill & \hfill {\displaystyle \text{ 81 }}\hfill & \hfill {\displaystyle \text{ 90 }}\hfill & \hfill {\displaystyle \text{ 84 }}\hfill \\ \hfill {\displaystyle \text{12. B }}\hfill & \hfill {\displaystyle \text{ 71 }}\hfill & \hfill {\displaystyle \text{ 76 }}\hfill & \hfill {\displaystyle \text{ 74 }}\hfill \\ \hfill {\displaystyle \text{átlag }}\hfill & \hfill {\displaystyle \text{ 79 }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math> }}\hfill & \hfill {\displaystyle }\hfill \\ \hline\end{array}}$   A 12. A osztályban $a$ fiú, a 12. B osztályban $b$ fiú, a 12. A osztályban $c$ lány, a 12. B osztályban $d$ lány van. A táblázat első sora alapján a következő egyenletet írhatjuk fel: $81a+90c=84\left(a+c\right)$, amelyből $a=2c$. A táblázat második sora alapján pedig a következő: $71b+76d=74\left(b+d\right)$, amelyből $d=1\mathrm{,}5b$. A táblázat első oszlopa alapján: $81a+71b=79\left(a+b\right)$, ebből $a=4b$. A táblázat második oszlopa alapján: $90c+76d=x\left(c+d\right)$,   vagyis $x=\frac{90c+76d}{c+d}$. Mivel $a=2c$ és $a=4b$, ezért $2c=4b$, vagyis $c=2b$. Alkalmazzuk az $x$-re kapott összefüggésben a $c=2b$ és a korábban kapott $d=1\mathrm{,}5b$ helyettesítést: $\begin{array}{c}{\displaystyle x=\frac{90\cdot 2b+76\cdot 1\mathrm{,}5b}{2b+1\mathrm{,}5b}=\frac{180+114}{3\mathrm{,}5}=84.}\end{array}$ A két osztályban az összes lány átlagpontszáma $84$. $b)$ Legyen András hat jegye: $a\le b\le c\le d\le e\le f$. Mivel ezeknek az érdemjegyeknek a mediánja $4$, és   páros darabszámú jegyről van szó, ezért $\frac{c+d}{2}=4$. Benedek hét jegyével kapcsolatban három eset lehetséges. Ha $c=3$ és $d=5$, akkor a sorrend: $a\mathrm{,}b\mathrm{,}c\mathrm{,5,}d\mathrm{,}e\mathrm{,}f\mathrm{,}$ vagyis a medián $5$. Ha $c=4$ és $d=4$, akkor a sorrend: $a\mathrm{,}b\mathrm{,}c\mathrm{,}d\mathrm{,}\text{...}\mathrm{,}$ vagyis a medián $d=4$-gyel egyenlő. Ezek alapján, ha a hat érdemjegyhez hozzáveszünk egy $5$-öst, akkor a hét számnak a mediánja, azaz Benedek matematikajegyeinek mediánja vagy $4$, vagy $5$ lesz. $c)$ A megfelelő félévi jegyet a következő táblázatban rögzítettük $\left(a\mathrm{,}b\mathrm{,}\text{...}\mathrm{,}i\in \left\{1;2;3;4;5\right\}\right)$: ${\displaystyle \begin{array}{|cccc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{ matematika }}\hfill & \hfill {\displaystyle \text{ fizika }}\hfill & \hfill {\displaystyle \text{ kémia }}\hfill \\ \hfill {\displaystyle \text{Anna }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math> }}\hfill \\ \hfill {\displaystyle \text{Bea }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>e</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi></math> }}\hfill \\ \hfill {\displaystyle \text{Cila }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>g</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>h</mi></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>i</mi></math> }}\hfill \\ \hline\end{array}}$   Anna átlaga: $\frac{a+b+c}{3}$, Bea átlaga: $\frac{d+e+f}{3}$, Cili átlaga: $\frac{g+h+i}{3}$. A három tanuló átlagának az átlaga: $\begin{array}{c}{\displaystyle \frac{\frac{a+b+c}{3}+\frac{d+e+f}{3}+\frac{g+h+i}{3}}{3}=\frac{a+b+c+d+e+f+g+h+i}{9}\mathrm{.}}\end{array}$ A matematika átlaga: $\frac{a+d+g}{3}$, a fizika átlaga: $\frac{b+e+h}{3}$, a kémia átlaga: $\frac{c+f+i}{3}$. A három tantárgy átlagának az átlaga: $\begin{array}{c}{\displaystyle \frac{\frac{a+d+g}{3}+\frac{b+e+h}{3}+\frac{c+f+i}{3}}{3}=\frac{a+b+c+d+e+f+g+h+i}{9}\mathrm{.}}\end{array}$ Láthatjuk, hogy a három tanuló átlagának az átlaga és a három tantárgy átlagának az átlaga egyenlő.