Cím:	Kunfalvi Rezső Olimpiai Válogatóverseny 1. elméleti forduló
Füzet:	2022/szeptember, 368 - 369. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Kunfalvi Rezső Olimpiai Válogatóverseny 1. elméleti forduló 2022. március 21. 15:00   Figyelem!${}^{*}$0 A versenyen nem-grafikus számológépen, író- és rajzeszközökön kívül semmilyen más segédeszköz (pl. könyv, füzet, táblázatok, internet) nem használható. A feladatok megoldását kézírással, papírra kell elkészíteni, minden feladat megoldása új oldalon kezdődjön. Az első oldalon szerepeljen a versenyző neve, évfolyama, felkészítő tanárainak és iskolájának neve. Törekedni kell a jól áttekinthető külalakra, az olvasható kézírásra, a megoldások fizikai alapjainak ismertetésére, valamint a magyaros, világos és tömör fogalmazásra. Minden feladat azonos pontszámot ér. A verseny időtartama 3 óra, amelynek lejárta után további 30 perc áll rendelkezésre a megoldások digitalizálására és elküldésére. A megoldásokat egyetlen pdf-dokumentumban a verseny napján (2022. március 21.) 18:30-ig kell elküldeni az iphoteamhun@gmail.com címre. A későn érkezett dolgozatokat nem tudjuk elfogadni. A pdf-dokumentum készülhet például mobiltelefonos alkalmazással vagy szkennerrel. 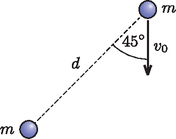  F1. Az ábrán látható két pontszerű, szabad elmozdulásra képes test között csak a tömegvonzás hat. Kezdetben a testek távolsága $d$, az egyik $m$ tömegű test nyugalomban van, a másik (ugyancsak $m$ tömegű) test pedig $v_0=k\sqrt[]{\gamma m/d}$ sebességgel mozog az ábrán látható irányban, ahol $k$ paraméter, $\gamma$ pedig a gravitációs állandó.     $a)$ Legalább mekkora $k$ értéke, ha a testek hosszú idő után egymástól nagyon messzire (,,végtelen'' távolra) kerülnek? $b)$ Mekkora a testek közötti legnagyobb távolság 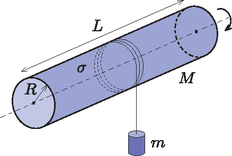$k=1$ esetén?   F2. Egy szigetelőanyagból készült, $R$ sugarú, $L$ hosszúságú ($L\gg R$), vékony falú, $M$ tömegű cső egyenletesen fel van töltve $\sigma$ felületi töltéssűrűséggel. A cső rögzített szimmetriatengelye körül súrlódásmentesen foroghat. A csőre fonalat csévélünk, melynek végére $m$ tömegű kis testet rögzítünk. Mekkora gyorsulással mozog a kis test, ha elengedjük?       F3. Az ábrán látható áramkörben a telepek, a dióda és a tekercs ideális. A K kapcsoló hosszú ideje zárva van. Adatok: $L=150$ mH, $C=200$ nF, $R=500\Omega$, $U_0=9\mathrm{,}0$ V. $a)$ Mekkora maximális $U_{\text{<span style="font-weight: normal;font-style: normal;">max</span>}}$ feszültségre töltődik fel a kondenzátor, miután a kapcsolót kinyitjuk? $b)$ A kapcsoló kinyitása után mennyi idővel éri el a kondenzátor feszültsége az $U_{\text{<sp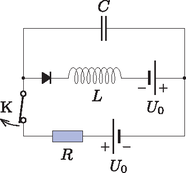an style="font-weight: normal;font-style: normal;">max</span>}}$ értéket?     F4. A pozitron egyszeresen pozitív töltésű elemi részecske, melynek tömege egyenlő az elektron $m_0$ tömegével. Egy állónak tekinthető elektronnak $3m_0{c}^2$ mozgási energiájú pozitront ütköztetünk, melynek következtében annihiláció következik be és az energia két foton formájában sugárzódik szét. $a)$ Feltéve, hogy a két foton ellentétes irányban repül szét, mekkora a fotonok hullámhosszának aránya? $b)$ Mekkora a két foton kirepülési iránya által bezárt szög lehetséges legkisebb értéke? 0 ${}^{*}$ A versenyzőknek szóló technikai információk itteni közlésével a későbbi, hasonló stílusban megrendezendő versenyek résztvevőit szeretnénk segíteni. (A Szerk.)