Cím:	Megoldásvázlatok a 2021/8. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Fridrik Richárd, Szeged
Füzet:	2021/december, 524 - 533. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg az alábbi egyenlőtlenséget a valós számok halmazán: $\begin{array}{c}{\displaystyle {\left(\frac{1}{3}\right)}^{x-1}+{\left(\frac{1}{3}\right)}^x+{\left(\frac{1}{3}\right)}^{x+1}<\frac{13}{27}\mathrm{.}}\end{array}$ (5 pont) $b)$ Oldjuk meg az alábbi egyenletet a $[\frac{\pi }{2};\frac{5\pi }{2}]$ intervallumon: $\begin{array}{c}{\displaystyle 1+4\text{sin}x-4\text{cos}{}^{2}x=0.}\end{array}$ (6 pont)   Megoldás. $a)$ Alkalmazzuk a hatványozás azonosságait: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(\frac{1}{3}\right)}^{x-1}+{\left(\frac{1}{3}\right)}^x+{\left(\frac{1}{3}\right)}^{x+1}=\frac{(\frac{1}{3}{)}^x}{\frac{1}{3}}+{\left(\frac{1}{3}\right)}^x+\frac{1}{3}\cdot {\left(\frac{1}{3}\right)}^x=\frac{13}{3}\cdot {\left(\frac{1}{3}\right)}^x<\frac{13}{27}\iff {\left(\frac{1}{3}\right)}^x<\frac{1}{9}\mathrm{.}}\hfill \end{array}}$ Tehát $(\frac{1}{3}{)}^x<\frac{1}{9}=(\frac{1}{3}{)}^2$. Az $f\left(x\right)=(\frac{1}{3}{)}^x$ függvény szigorúan monoton csökkenő, ezért a nagyobb értéket a kisebb helyen veszi fel, azaz a megoldás $x>2$. $b)$ Használjuk fel, hogy $\text{cos}{}^{2}x=1-\text{sin}{}^{2}x$. Ekkor $\begin{array}{c}{\displaystyle 1+4\text{sin}x-4\cdot \left(1-\text{sin}{}^{2}x\right)=0\Rightarrow 4{\text{sin}}^{2}x+4\text{sin}x-3=0.}\end{array}$ Ez $\text{sin}x$-ben egy másodfokú egyenlet, megoldásai: $\text{sin}x=\frac{-3}{2}$ vagy $\text{sin}x=\frac{1}{2}$. 1. eset: Ha $\text{sin}x=\frac{-3}{2}$. Ennek nincs megoldása, mert $\forall x\in \text{R}$ esetén $-1\le \text{sin}x\le 1$. 2. eset: Ha $\text{sin}x=\frac{1}{2}$. Mivel $x\in [\frac{\pi }{2};\frac{5\pi }{2}]$, ezért $x_1=\frac{5\pi }{6}$ és $x_2=\frac{13\pi }{6}$. Tehát a megoldások $x_1=\frac{5\pi }{6}$ és $x_2=\frac{13\pi }{6}$. Ellenőrzés vagy ekvivalenciára való hivatkozás.   2. $a)$ Kata és Máté nemrég tanulták az iskolában az osztókat. Kitaláltak egy játékot. A játékot Kata kezdi és felváltva mondanak az $n$ pozitív egész szám osztói közül egyet úgy, hogy olyan osztót nem mondhatnak, amely korábban már elhangzott. Az veszít, aki már nem tud újabb osztót mondani. Hány olyan $n$ pozitív egész szám van az $\left\{1;2;3;\text{...};25\right\}$ halmazban, amely esetén Kata nyer? (4 pont) $b)$ Hány olyan $n$ pozitív egész szám van a $\left\{1;2;3;\text{...};2021\right\}$ halmazban, amelyre igaz, hogy $2^{n+3}+2^n$ négyzetszám? (5 pont) $c)$ Adjuk meg a $p$ valós paraméter lehetséges értékeit, ha az alábbi polinom összevont alakjában a másodfokú tag együtthatója $-3$: $\begin{array}{c}{\displaystyle {\left(x-1\right)}^2\cdot {\left(p+2x\right)}^2\mathrm{.}}\end{array}$ (5 pont)   Megoldás. $a)$ I. megoldás. Kata pontosan akkor nyer, ha az osztók száma páratlan. Egy szám osztói osztópárokba rendezhetők. Ha az osztók száma páratlan, akkor valamely osztónak önmaga a párja. Tehát a szám négyzetszám. Az $\left\{1;2;3;\text{...};25\right\}$ halmazban a négyzetszámok: 1; 4; 9; 16; 25. Ezek száma 5. Tehát 5 olyan szám van, amely esetén Kata nyer. II. megoldás. Kata pontosan akkor nyer, ha az osztók száma páratlan. Ha az $n$ szám kanonikus alakja $n=p_1^{{\alpha }_1}\cdot p_2^{{\alpha }_2}\cdot \text{...}\cdot p_k^{{\alpha }_k}$, akkor osztóinak száma $\begin{array}{c}{\displaystyle \left({\alpha }_1+1\right)\cdot \left({\alpha }_2+1\right)\cdot \text{...}\cdot \left({\alpha }_k+1\right)\mathrm{.}}\end{array}$ Az osztók száma páratlan, ezért ${\alpha }_1;{\alpha }_2;\text{...};{\alpha }_k$ mindegyike páros. Tehát $n=p_1^{{2\beta }_1}\cdot p_2^{2{\beta }_2}\cdot \text{...}\cdot p_k^{2{\beta }_k}=(p_1^{{\beta }_1}\cdot p_2^{{\beta }_2}\cdot \text{...}\cdot p_k^{{\beta }_k}{)}^2$, azaz négyzetszám. Az $\left\{1;2;3;\text{...};25\right\}$ halmazban a négyzetszámok: 1; 4; 9; 16; 25. Ezek száma 5. Tehát 5 olyan szám van, amely esetén Kata nyer.   Megjegyzés. Akár végig is lehet próbálni az összes számot és a végére juthatunk így is a feladatnak.   $b)$ I. megoldás. Mivel $2^{n+3}+2^n=8\cdot 2^n+2^n=9\cdot 2^n$ és a $9$ négyzetszám, ezért a kifejezés pontosan akkor lesz négyzetszám, ha $2^n$ négyzetszám. Ez akkor teljesül, ha $n$ páros szám. Az $\left\{1;2;3;\text{...};2021\right\}$ halmazban $1010$ darab páros szám van. II. megoldás. Ha $n=1$, akkor a kifejezés értéke 18, ami nem négyzetszám. Ha $n=2$, akkor a kifejezés értéke 36, ami négyzetszám. Vegyük észre, hogy ha $n$ értékét egyesével növeljük, akkor a kifejezés értéke mindig a kétszeresére növekszik, ugyanis $\begin{array}{c}{\displaystyle 2^{n+4}+2^{n+1}=2\cdot 2^{n+3}+2\cdot 2^n=2\cdot \left(2^{n+3}+2^n\right)\mathrm{.}}\end{array}$ Tehát, ha valamely $n$-re a kifejezés négyzetszám, akkor $\left(n+2\right)$-re is négyzetszám. És nyilván, ha valamely $n$-re a kifejezés nem négyzetszám, akkor $\left(n+2\right)$-re sem négyzetszám. Ezért a számunkra megfelelő értékek $n\in \left\{2;4;6;\text{...};2020\right\}$. Tehát 1010 megoldás van, amely megfelel nekünk. $c)$ Bontsuk fel a zárójeleket és rendezzük a polinomot a változó csökkenő hatványai szerint: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle g\left(x\right)}& {\displaystyle ={\left(x-1\right)}^2\cdot {\left(p+2x\right)}^2=\left(x^2-2x+1\right)\cdot \left(4x^2+4px+p^2\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =4x^4+\left(4p-8\right)x^3+\left(p^2-8p+4\right)x^2+\left(4p-2p^2\right)x+p^2\mathrm{.}}\hfill \end{array}}$ A másodfokú tag együtthatója $p^2-8p+4$, ezért meg kell oldjuk az $p^2-8p+4=-3$ egyenletet. Ennek a megoldásai: $p_1=1$ és $p_2=7$.   Megjegyzés. Nem feltétlenül kellett volna összeszorozni minden tagot minden taggal, hiszen másodfokú tag csak úgy keletkezhet, ha másodfokút konstanssal vagy elsőfokút elsőfokúval szorzunk.   3. $a)$ Egy dobozban van $7$ különböző pár kesztyű. A dobozból egyesével, visszatevés nélkül húzunk ki kesztyűket mindaddig, amíg nem kapunk egy pár kesztyűt. Mennyi annak a valószínűsége, hogy ehhez legfeljebb $3$-szor kell húzzunk a dobozból? (7 pont) $b)$ Az iskola $11.$-es és $12.$-es legjobb $12$ matekos diákjának nemek szerinti és évfolyam szerinti eloszlását a táblázat tartalmazza. ${\displaystyle \begin{array}{|ccc|}\hline \multicolumn{1}{c}{{\displaystyle }}& \hfill {\displaystyle \text{11.-es}}\hfill & \hfill {\displaystyle \text{12.-es}}\hfill \\ \hfill {\displaystyle \text{Fiúk}}\hfill & \hfill {\displaystyle \text{4}}\hfill & \hfill {\displaystyle \text{3}}\hfill \\ \hfill {\displaystyle \text{Lányok}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{3}}\hfill \\ \hline\end{array}}$ A tanáruk véletlenszerűen választott közülük diákokat a körzeti matekversenyre. A verseny szabályzata szerint egy csapatban ketten indulnak $($a csapattagok között nincs kitüntetettség$)\mathrm{,}$ akik közül legalább az egyikük lány $($akár mindkettő résztvevő lehet lány$)$ és a két résztvevő nem lehet ugyanarról az évfolyamról. Mennyi annak a valószínűsége, hogy a tanáruk a versenyszabályzatnak megfelelő nevezést adott le? Eredményünket $3$ tizedesjegyre kerekítve adjuk meg. (5 pont)   Megoldás. $a)$ Két olyan eset van, amikor legfeljebb 3 húzásból lesz egy pár kesztyű a kihúzottak között. 1. eset: Ha második húzásra egy pár kesztyű lesz nálunk. Ennek a valószínűsége $\begin{array}{c}{\displaystyle \frac{14\cdot 1}{14\cdot 13}=\frac{1}{13}\mathrm{,}}\end{array}$ ugyanis elsőre még bármit húzhatunk, másodikra pedig csak annak a párját tudjuk húzni. 2. eset: Ha a harmadik húzásra lesz meg az első pár kesztyű. Ennek a valószínűsége $\begin{array}{c}{\displaystyle \frac{14\cdot 12\cdot 2}{14\cdot 13\cdot 12}=\frac{2}{13}\mathrm{,}}\end{array}$ ugyanis elsőre bármit húzhatunk, másodikra nem húzhatjuk annak a párját, tehát 12 közül húzhatunk, majd harmadikra az egyik már kihúzott kesztyűnek kell a párját kihúzni. Tehát a keresett valószínűség $\begin{array}{c}{\displaystyle P\left(\text{legfeljebb 3 húzás elég}\right)=\frac{1}{13}+\frac{2}{13}=\frac{3}{13}\mathrm{.}}\end{array}$ Megjegyzés. Az első esetnél azonnal tudtuk volna mondani az $\frac{1}{13}$ valószínűséget, ugyanis az első kesztyű még bármi lehet és marad 13 kesztyű a dobozban. Ez a 13 az összes eset száma és csak 1 kedvező van: ha az először kihúzottnak a párját húzzuk másodiknak. $b)$ Az összes eset száma $\left(\genfrac{}{}{0ex}{}{12}{2}\right)=66$. Az alábbi összeállítások esetén ad le jó nevezést a tanár: 1. eset: 11.-es lány és 12.-es lány. Ekkor a kedvező esetek száma $2\cdot 3=6$. 2. eset: 11.-es lány és 12.-es fiú. Ekkor a kedvező esetek száma $2\cdot 3=6$. 3. eset: 12.-es lány és 11.-es fiú. Ekkor a kedvező esetek száma $3\cdot 4=12$. $P\left(\text{jó a nevezés}\right)=\frac{6+6+12}{66}=\frac{4}{11}$, ami 3 tizedesjegyre kerekítve 0,364.   4. Adott az $x^2+y^2+18x-4y+45=0$ egyenletű $k$ kör. $a)$ Igazoljuk, hogy a $k$ kör középpontjának koordinátái $K\left(-9;2\right)$. (2 pont) $b)$ Határozzuk meg a $k$ kör $P\left(-7;8\right)$ pontjába húzható érintőjének egyenletét. (3 pont) $c)$ Adottak az $A\left(1;1\right)$, $B\left(10;4\right)$, $C\left(2;8\right)$ pontok. Mutassuk meg, hogy a három pont által meghatározott háromszög köré írható körének középpontja illeszkedik az $x+3y=17$ egyenletű egyenesre. (9 pont)   Megoldás. $a)$ Teljes négyzetté alakítást hajtunk végre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x^2+y^2+18x-4y+45}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle {\left(x+9\right)}^2-81+{\left(y-2\right)}^2-4+45}& {\displaystyle =0.}\hfill \end{array}}$ Azaz ${\left(x+9\right)}^2+{\left(y-2\right)}^2=40$. Innen a kör középpontja leolvasható: $K\left(-9;2\right)$. $b)$ Az érintőnek adott a $P\left(-7;8\right)$ pontja. Ez valóban pontja a körnek, amiről a koordináták behelyettesítésével meggyőződhetünk. Egy normálvektora a $\overrightarrow{KP}\left(2;6\right)$ vektor. Az érintő egyenlete $\begin{array}{c}{\displaystyle 2x+6y=2\cdot \left(-7\right)+6\cdot \mathrm{8,}}\end{array}$ azaz egyszerűsítve $x+3y=17$. $c)$ A háromszög köré írt körének középpontját az oldalfelező merőlegesek metszéspontjaként kapjuk meg. Elég két oldalfelezési pont: $F_a\left(6;6\right)$ és $F_c(\frac{11}{2};\frac{5}{2})$. Az $F_a$ ponton áthaladó $e$ oldalfelező merőleges egy normálvektora ${\overrightarrow{n}}_e=\overrightarrow{CB}\left(8;-4\right)$, egyenlete $2x-y=6$. Az $F_c$ ponton áthaladó $f$ oldalfelező merőleges egy normálvektora $\begin{array}{c}{\displaystyle {\overrightarrow{n}}_f=\overrightarrow{AB}\left(9;3\right)\mathrm{,}}\end{array}$ egyenlete $3x+y=19$. Legyen $O$ a háromszög köré írt kör középpontja. Ekkor $e\cap f=\left\{O\right\}$, azaz meg kell oldani az alábbi egyenletrendszert: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2x-y}& {\displaystyle =\mathrm{6,}}\hfill \\ \hfill {\displaystyle 3x+y}& {\displaystyle =19.}\hfill \end{array}}$ Ennek megoldása $x=5$; $y=4$. Tehát $O\left(5;4\right)$. Ez a pont valóban illeszkedik az $x+3y=17$ egyenletű egyenesre, ugyanis $5+3\cdot 4=17$.   II. rész     5. Egy derékszögű háromszög oldalaiból álló minta terjedelme $18$ egység, a medián $24$ egység. $a)$ Igazoljuk, hogy a háromszög oldalainak hossza $7$; $24$ és $25$ egység. (5 pont) $b)$ Adjuk meg a háromszög beírt és köré írt körének középpontjának távolságát. (7 pont) A fenti háromszög befogóin megjelöljük azokat a belső osztópontokat, amelyek a derékszögű csúcstól egész egység távolságra helyezkednek el. $c)$ Hány olyan háromszög adható meg, melyeknek csúcsai ezen belső osztópontok közül kerülnek ki? (4 pont)   Megoldás. $a)$ A háromszög három oldala legyen nagyság szerint rendezve $a\le b<c$. Mivel a medián 24, ezért $b=24$. Mivel a terjedelem 18, ezért $c=a+18$. Pitagorasz tétele szerint $a^2+{24}^2={\left(a+18\right)}^2$. Ezt megoldva kapjuk, hogy $a=7$. Tehát a háromszög oldalainak hossza valóban 7; 24 és 25 egység. $b)$ I. megoldás. Az $ABC$ háromszög területe $T=\frac{7\cdot 24}{2}=84$. Félkerülete $s=28$, ezért beírt körének sugara $r=\frac{T}{s}=3$. Az $OECD$ négyszög négyzet, ezért $CD=3$, így $BD=4$. Külső pontból körhöz húzott érintőszakaszok hossza egyenlő, ezért $BF=BD=4$. Thálész tételének megfordítása miatt a háromszög köré írt kör középpontja az átfogó felezőpontja és a kör sugara $R=\frac{c}{2}=12\mathrm{,}5$. Mivel $BK=12\mathrm{,}5$ és $BF=4$, ezért $KF=8\mathrm{,}5$. A $KFO$ háromszög derékszögű, ezért Pitagorasz tétele szerint 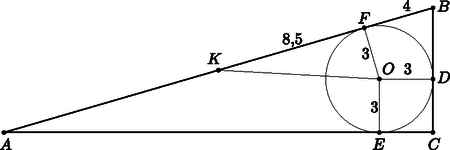$\begin{array}{c}{\displaystyle {KO}^2={8\mathrm{,}5}^2+3^2\Rightarrow KO=\frac{\sqrt[]{325}}{2}\approx 9\mathrm{,}01.}\end{array}$   Megjegyzés. A háromszög beírt köre sugarának hosszát megkaphattuk volna a csak derékszögű háromszögekre érvényes $r=\frac{a+b-c}{2}$ képlettel is. Ekkor szintén $\begin{array}{c}{\displaystyle r=\frac{7+24-25}{2}=3}\end{array}$ adódik.     II. megoldás. Helyezzük el a háromszöget derékszögű koordinátarendszerben, a csúcsok legyenek $A\left(0;0\right)$, $B\left(24;7\right)$, $C\left(24;0\right)$. Thalész tételének megfordítása miatt a háromszög köré írt kör középpontja az átfogó felezőpontja, azaz $K(12;\frac{7}{2})$. Az $ABC$ háromszög területe $T=\frac{7\cdot 24}{2}=84$. Félkerülete $s=28$, ezért beírt körének sugara $r=\frac{T}{s}=3$, és így a beírt kör középpontjának koordinátái $O\left(21;3\right)$. A feladat kérdése az $KO$ távolság meghatározása: 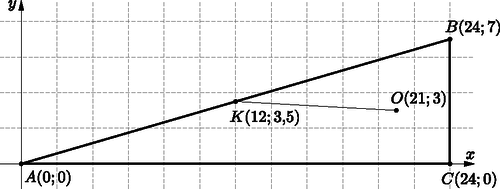$KO=\frac{\sqrt[]{325}}{2}\approx 9\mathrm{,}01$.     $c)$ I. megoldás. A hosszabb befogón 23 darab, a rövidebb befogón pedig 6 osztópont található. Háromszög akkor jön létre, ha az egyik befogó pontjai közül kettőt és a másik befogó pontjai közül egyet kiválasztunk. A háromszögek száma $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{23}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{6}{1}\right)+\left(\genfrac{}{}{0ex}{}{23}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{6}{2}\right)=1518+345=1863.}\end{array}$ II. megoldás. A hosszabb befogón 23 darab, a rövidebb befogón pedig 6 osztópont található. Komplementer módszerrel dolgozunk. Az összes ponthármasok száma $\left(\genfrac{}{}{0ex}{}{29}{3}\right)=3654$. A rossz esetek jelenleg azt jelentik, hogy a kiválasztott 3 pont egy egyenesre illeszkedik. Ezek száma $\left(\genfrac{}{}{0ex}{}{23}{3}\right)+\left(\genfrac{}{}{0ex}{}{6}{3}\right)=1771+20=1791$. A háromszögek száma $\begin{array}{c}{\displaystyle 3654-1791=1863.}\end{array}$   6. $a)$ Ottónak $55$ emelt matekos diákja van, akikkel tesztet írat koordinátageometriából. A teszten $3$ kérdés van és minden egyes kérdésre $3$ válaszlehetőség, melyek közül pontosan $1$ helyes válasz van. Mutassuk meg, hogy van legalább $3$ olyan diák, akik pontosan ugyanúgy töltötték ki a tesztet. (Két tesztkitöltést akkor tekintünk azonosnak, ha az egyes kérdésekre adott válasz minden egyes esetben megegyezik.) (5 pont) $b)$ A fenti $55$ diák közül András, Bogi, Csaba, Dani, Emese, Feri, Gizi és Huba úgy töltötték ki a teszt első kérdését, hogy minden egyes válaszlehetőség legalább egyszer előfordult a válaszaik között $(3$ válaszlehetőség volt minden egyes kérdésre$)$. Hányféle különböző kitöltést tud adni a $8$ tanuló csak az első kérdésre, ha csak az számít, hogy az egyes válaszlehetőségeket hányan jelölték meg? (6 pont) $c)$ A diákok közül Ilona, József, Kati, Laci, Marci és Nóri nagyon rosszul teljesítettek a teszten, ezért Ottó úgy döntött, hogy a jobb teljesítés érdekében alakítsanak ki tanulópárokat $($azaz $2$ diákból álló csoportokat$)$. Hányféleképpen alakíthat ki a $6$ diák tanulópárokat, ha az egyes tanulópárok között és a tanulópárokon belül sincs kitüntetettség a diákok között? (5 pont)   Megoldás. $a)$ Mindhárom kérdésre egymástól függetlenül háromféleképpen válaszolhatnak a diákok, ezért a tesztet $3^3=27$ különböző módon lehet kitölteni. Mivel $55=2\cdot 27+1$, ezért a skatulyaelv szerint biztosan lesz legalább 3 olyan diák, akik pontosan ugyanúgy töltötték ki a tesztet. $b)$ I. megoldás. A feladat feltétele szerint mindegyik válaszlehetőséget legalább egy diák megjelölte, ezért lényegében az a feladatunk, hogy a maradék 5 diákot osszuk szét. Az alábbi esetek adódnak: 1. eset: $5+0+0$, ebből 3 lehetőségünk van. 2. eset: $4+1+0$, ebből 6 lehetőségünk van. 3. eset: $3+2+0$, ebből 6 lehetőségünk van. 4. eset: $3+1+1$, ebből 3 lehetőségünk van. 5. eset: $2+2+1$, ebből 3 lehetőségünk van. Tehát összesen 21 különböző kitöltést tud adni a 8 diák. II. megoldás. Az egyes válaszlehetőségekre érkezzen rendre $x$; $y$; $z$ válasz. Ekkor $x$; $y$; $z$ olyan pozitív egész számok, amelyekre $x+y+z=8$. Képzeljük el azt, hogy 8 almát (az ábrán a pöttyök szemléltetik az almákat) osztunk szét három gyerek között, akik mindegyike kap legalább egy almát. Annyiféleképpen tudjuk felbontani a 8-at három összeadandóra, ahányféleképpen a köztük lévő 7 résnél elhelyezünk két összeadás jelet. Ezek száma 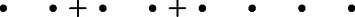$\left(\genfrac{}{}{0ex}{}{7}{2}\right)=21$.     $c)$ I. megoldás. A rosszul teljesítő diákok legyenek $A$; $B$; $C$; $D$; $E$; $F$. Először keressünk tanulópárt $A$-nak. A többi 5 diák közül akármelyik lehet a párja, ez 5 lehetőség, legyen pl. $B$. Most keressünk tanulópárt $C$-nek. A többi 3 diák közül akármelyik lehet a párja, ez 3 lehetőség, legyen pl. $D$. A maradék két diák pedig egy párt alkot. Az összes lehetőségek száma $5\cdot 3\cdot 1=15$. II. megoldás. Először a 6 diákból kijelölünk egy párt. Ezt $\left(\genfrac{}{}{0ex}{}{6}{2}\right)=15$-féle módon tehetjük meg. A maradék 4 diákból kiválasztunk egy másik párt, ezt $\left(\genfrac{}{}{0ex}{}{4}{2}\right)=6$ különböző módon tehetjük meg. A megmaradt 2 tanuló pedig egy párt fog alkotni. Ekkor minden párt $3!=6$-szor számoltunk meg, ezért az összes lehetőségek száma $\frac{15\cdot 6}{6}=15$.   Megjegyzés. Ha 6 helyett $2n$ számú diákot kellene párokba rendezni, akkor azt az első megoldás alapján $1\cdot 3\cdot 5\cdot \text{...}\cdot \left(2n-1\right)$-féle módon tehetnénk meg. A második megoldás alapján pedig $\begin{array}{c}{\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{2}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{4}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{6}{2}\right)\cdot \text{...}\cdot \left(\genfrac{}{}{0ex}{}{2n}{2}\right)}{n!}}\end{array}$ féle módon. Ebből adódik, hogy tetszőleges pozitív egész $n$ esetén: $\begin{array}{c}{\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{2}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{4}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{6}{2}\right)\cdot \text{...}\cdot \left(\genfrac{}{}{0ex}{}{2n}{2}\right)}{n!}=1\cdot 3\cdot 5\cdot \text{...}\cdot \left(2n-1\right)\mathrm{.}}\end{array}$   7. Szorgalmas Szonja elhatározza, hogy koordinátageometriai hiányosságait szorgos gyakorlással orvosolja. Ezért minden egyes nap megold $20$ ilyen jellegű feladatot. Még nem megy neki olyan jól, ugyanis minden nap csak $5$ feladatot tud helyesen megoldani. Egy héten át minden egyes nap megkéri Lusta Lujzát, hogy ellenőrizze le mind a $20$ feladatot. Lujza nem nézi végig az összes feladatot. Minden egyes nap csak $3$, általa véletlenszerűen kijelöltet ellenőriz le. $a)$ Mutassuk meg, hogy három tizedesjegyre kerekítve 0,601 annak a valószínűsége, hogy az adott napon a $3$ ellenőrzött feladatból lesz helyesen megoldott feladata Szonjának. (4 pont) $b)$ Mennyi annak a valószínűsége, hogy a $7$ nap alatt legfeljebb egyszer fordul elő az, hogy lesz helyesen megoldott feladata Szonjának? Válaszunkat $4$ tizedesjegyre kerekítve adjuk meg. (5 pont) $c)$ Legalább hány napon keresztül kell Lujzának átnéznie a feladatokat az ő sajátos módszerével, hogy legalább $99\mathrm{,}99\%$-os valószínűséggel legyen olyan nap, amikor van helyesen megoldott feladata Szonjának? (7 pont)   Megoldás. $a)$ Komplementer módszerrel fogunk dolgozni. $\begin{array}{c}{\displaystyle P\left(\text{lesz jó feladat}\right)=1-P\left(\text{mindhárom rossz}\right)=1-\frac{\left(\genfrac{}{}{0ex}{}{15}{3}\right)}{\left(\genfrac{}{}{0ex}{}{20}{3}\right)}=\frac{137}{228}\mathrm{,}}\end{array}$ ami 3 tizedesjegyre kerekítve 0,601. $b)$ Mivel $P\left(\text{lesz jó feladat}\right)\approx 0\mathrm{,}601$, ezért $P\left(\text{mindegyik rossz}\right)\approx 0\mathrm{,}399$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle P\left(\text{legfeljebb egyszer lesz jó feladat}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =P\left(\text{7 csak rossz}\right)+P\left(\text{1 van jó és 6 csak rossz}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={0\mathrm{,}399}^7+\left(\genfrac{}{}{0ex}{}{7}{1}\right)\cdot 0\mathrm{,}601\cdot {0\mathrm{,}399}^6\approx 0\mathrm{,}018\mathrm{58,}}\hfill \end{array}}$ ami 4 tizedesjegyre kerekítve 0,0186. $c)$ Lujza a feladatokat $n$ napon keresztül nézze át. Ekkor a feltétel szerint $\begin{array}{c}{\displaystyle P\left(\text{van jó feladatos nap}\right)\ge 0\mathrm{,}9999\Rightarrow 1-P\left(\text{<span style="font-weight: normal;font-style: normal;">mindegyik rossz</span>}\right)\ge 0\mathrm{,}\mathrm{9999,}}\end{array}$ azaz $0\mathrm{,}0001\ge P\left(\text{mindegyik rossz}\right)={0\mathrm{,}399}^n$. Tehát meg kell oldjuk a $0\mathrm{,}0001\ge {0\mathrm{,}399}^n$ egyenlőtlenséget. Vegyük mindkét oldal 10-es alapú logaritmusát és vegyük figyelembe, hogy ez szigorúan monoton növekvő függvény. Alkalmazzuk a logaritmus azonosságot: $\begin{array}{c}{\displaystyle 0\mathrm{,}0001\ge {0\mathrm{,}399}^n\Rightarrow \text{lg}0\mathrm{,}0001\ge \text{lg}{0\mathrm{,}399}^n\Rightarrow -4\ge n\cdot \text{lg}0\mathrm{,}399.}\end{array}$ Mivel $\text{lg}0\mathrm{,}399<0$, ezért az osztáskor fordul a relációsjel iránya. $\frac{-4}{\text{lg}0\mathrm{,}399}\le n\mathrm{,}$ azaz $10\mathrm{,}02\le n$. Tehát Lujzának legalább 11 napon keresztül kell átnéznie Szonja feladatait a feltétel teljesüléséhez.   8. $a)$ Egy számtani sorozat első $9$ tagjának összege $198$. Mekkora a sorozat első tagja és differenciája, ha az első $18$ tagjának összege $639?$ (4 pont) $b)$ Egy mértani sorozat hányadosa $2$. A sorozat $n$-edik tagja $16$ és az első $n$ tag összege $31\mathrm{,}75$. Határozzuk meg $n$ értékét. (5 pont) $c)$ Igazoljuk, hogy az $a_n=\frac{1}{n+1}+\frac{1}{n+2}+\text{...}+\frac{1}{2n}$ sorozat szigorúan monoton növekedő. (5 pont) $d)$ Adjuk meg az $a_n=\frac{1}{n+1}+\frac{1}{n+2}+\text{...}+\frac{1}{2n}$ sorozat legkisebb tagját. (2 pont)   Megoldás. $a)$ Ismert, hogy $S_n=\frac{2a_1+\left(n-1\right)\cdot d}{2}\cdot n$, ezért $S_9=\frac{2a_1+8d}{2}\cdot 9$ és $S_{18}=\frac{2a_1+17d}{2}\cdot 18$. Tehát a feladat szövege szerint $2a_1+8d=44$ és $2a_1+17d=71$. Ez egy elsőfokú, lineáris egyenletrendszer, melyet pl. megoldhatunk úgy, hogy kivonjuk egymásból a két egyenletet. Kapjuk, hogy $\left(2a_1+17d\right)-\left(2a_1+8d\right)=71-44$, azaz $d=3$. Innen $a_1=10$ adódik. Ellenőrzés a feladat szövege alapján. $b)$ I. megoldás. Felhasználjuk, hogy $a_n=a_1\cdot q^{n-1}$ és $q\ne 1$ esetén $S_n=a_1\cdot \frac{q^n-1}{q-1}$. Tehát $a_1\cdot 2^{n-1}=16$ és $a_1\cdot \frac{2^n-1}{2-1}=31\mathrm{,}75$. Azaz $a_1\cdot 2^n=32$ és $a_1\cdot \left(2^n-1\right)=31\mathrm{,}75$. Innen kapjuk, hogy $a_1\cdot 2^n-a_1=31\mathrm{,}75$, tehát $32-a_1=31\mathrm{,}75\Rightarrow a_1=0\mathrm{,}25$. Adódik, hogy $0\mathrm{,}25\cdot 2^{n-1}=16$. Ez az exponenciális egyenlet átírható $2^{-2}\cdot 2^{n-1}=2^4$ alakba, ahonnan már könnyen adódik, hogy $n=7$. Ellenőrzés a feladat szövege alapján. II. megoldás. Mivel $a_n=16$ és $q=2$, ezért $a_{n-1}=8$; $a_{n-2}=4$; $a_{n-3}=2$ stb. Nyilván mindig pozitív tagokat kapunk, ezért elég azt megnézni, hogy meddig kell összeadni visszafelé ezeket a tagokat, hogy megkapjuk az $S_n=31\mathrm{,}75$ értéket. Mivel $16+8+4+2+1+0\mathrm{,}5+0\mathrm{,}25=31\mathrm{,}75$, ezért $n=7$. Ellenőrzés a feladat szövege alapján. $c)$ Feladatunk megmutatni, hogy minden $n\in {\text{N}}^{+}$ esetén teljesül, hogy $a_{n+1}>a_n$. Ez ekvivalens azzal, hogy minden $n\in {\text{N}}^{+}$ esetén teljesül, hogy $a_{n+1}-a_n>0$. Ha $\begin{array}{c}{\displaystyle a_n=\frac{1}{n+1}+\frac{1}{n+2}+\cdots +\frac{1}{2n}\mathrm{,}\text{akkor}{a}_{n+1}=\frac{1}{n+2}+\cdots +\frac{1}{2n}+\frac{1}{2n+1}+\frac{1}{2n+2}\mathrm{.}}\end{array}$ Ekkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle a_{n+1}-a_n=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(\frac{1}{n+2}+\cdots +\frac{1}{2n}+\frac{1}{2n+1}+\frac{1}{2n+2}\right)-\left(\frac{1}{n+1}+\frac{1}{n+2}+\cdots +\frac{1}{2n}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}=\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{2}{2n+2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2n+1}-\frac{1}{2n+2}=\frac{1}{\left(2n+1\right)\left(2n+2\right)}>0.}\hfill \end{array}}$ Tehát megmutattuk, hogy a sorozat szigorúan monoton növekedő. $d)$ Mivel a $c)$ feladatrész szerint a sorozat szigorúan monoton növekedő, ezért a legkisebb tagja éppen $a_1=\frac{1}{2}$.   9. Adott az $3$; $4$; $5$; $x+7$; $11-x$ öt elemből álló minta. $a)$ Mutassuk meg, hogy a minta szórásnégyzete $\frac{2x^2-8x+40}{5}$. (A minta szórásnégyzete a minta szórásának a négyzete.) (5 pont) $b)$ Írjuk fel az $f\left(x\right)=\frac{2x^2-8x+40}{5}$ függvénynek az $x_0=7$ abszcisszájú pontjába húzható érintőjének az egyenletét. (Abszcissza: a pont első koordinátája.) (5 pont) $c)$ Mekkora területet zár közre az $x$ tengely, az $x=0;$ $x=6$ egyenes és az $f\left(x\right)=\frac{2x^2-8x+40}{5}$ függvény? (6 pont)   Megoldás. $a)$ I. megoldás. Az átlaguk $\overline{x}=\frac{3+4+5+\left(x+7\right)+\left(11-x\right)}{5}=6$. A szórásnégyzet ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\sigma }^2}& {\displaystyle =\frac{{\left(\overline{x}-x_1\right)}^2+\text{...}+{\left(\overline{x}-x_5\right)}^2}{5}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{{\left(6-3\right)}^2+{\left(6-4\right)}^2+{\left(6-5\right)}^2+{\left[6-\left(x+7\right)\right]}^2+{\left[6-\left(11-x\right)\right]}^2}{5}\mathrm{.}}\hfill \end{array}}$ Azaz $\begin{array}{c}{\displaystyle {\sigma }^2=\frac{9+4+1+\left(x^2+2x+1\right)+\left(x^2-10x+25\right)}{5}=\frac{2x^2-8x+40}{5}\mathrm{.}}\end{array}$ II. megoldás. Az átlaguk $\overline{x}=\frac{3+4+5+\left(x+7\right)+\left(11-x\right)}{5}=6$. A szórásnégyzet ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\sigma }^2}& {\displaystyle =\frac{x_1^2+x_2^2+x_3^2+x_4^2+x_5^2}{5}-{\overline{x}}^2=\frac{3^2+4^2+5^2+{\left(x+7\right)}^2+{\left(11-x\right)}^2}{5}-6^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{9+16+25+\left(x^2+14x+49\right)+\left(x^2-22x+121\right)}{5}-36=\frac{2x^2-8x+40}{5}\mathrm{.}}\hfill \end{array}}$ $b)$ Mivel $f\left(7\right)=\frac{2{\cdot 7}^2-8\cdot 7+40}{5}=16\mathrm{,}4$ és $f\text{'}\left(x\right)=\frac{4x-8}{5}\Rightarrow f\text{'}\left(7\right)=\frac{4\cdot 7-8}{5}=4$, ezért az érintő egyenlete az $y-f\left(x_0\right)=f\text{'}\left(x_0\right)\cdot \left(x-x_0\right)$ iránytényezős egyenlet alapján $y-16\mathrm{,}4=4\cdot \left(x-7\right)$, azaz $y=4x-11\mathrm{,}6$. $c)$ A függvénynek nincs valós zérushelye. Ezt a megoldóképletből kapjuk vagy abból, hogy az $a)$ feladat szerint egy nem állandó mintának a szórásnégyzetéről van szó. Használjuk a Newton‐Leibniz tételt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle ={\int }_0^{6}f\left(x\right)\text{d}x={\int }_0^6\frac{2x^2-8x+40}{5}dx={\left[\frac{2}{15}{x}^3-\frac{4}{5}{x}^2+8x\right]}_0^6=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(\frac{2}{15}\cdot 6^3-\frac{4}{5}{\cdot 6}^2+8\cdot 6\right)-\left(0\right)=48.}\hfill \end{array}}$