Cím:	Megoldásvázlatok a 2021/7. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Kozma Katalin Abigél, Győr
Füzet:	2021/november, 465 - 475. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. A karát egy viszonyszám, amely megmutatja, hogy mekkora az aranyötvözetben az arany tömegaránya. $a)$ Hány gramm ezüstöt tartalmaz egy $10$ karátos 0,06 kg tömegű nyaklánc, amely csak aranyat és ezüstöt tartalmaz, ha a színarany $24$ karátos? (2 pont) $b)$ Hány gramm aranyat olvasszon a nyaklánchoz az ötvös, ha $18$ karátos ötvözetet szeretne létrehozni? (4 pont) $c)$ Az ötvösmester pontosan $25$ éve hordja az egyik aranygyűrűjét, és megállapította, hogy időközben a gyűrű aranytartalmának tömege 0,012 milligrammal csökkent. Számítsuk ki, hogy naponta hány aranyatom vált le a gyűrűről, ha 197 gramm arany hozzávetőlegesen $6\cdot {10}^{23}$ darab aranyatomot tartalmaz. (Feltételezzük, hogy a kopás egyenletesen ment végbe, és tudjuk, hogy ezen időszakban $5$ szökőév volt.) (6 pont)   Megoldás. $a)$ A tízkarátos ötvözet tömegének $\frac{10}{24}$ része arany, $\frac{14}{24}$ része ezüst, tehát a nyaklánc ezüsttartalma $60\cdot \frac{14}{24}=35$ gramm. $b)$ 1. megoldás. Ha $x$ gramm aranyat olvasztunk hozzá, akkor a teljes tömeg $60+x$ gramm, az arany tömege pedig $25+x$ grammra nő, amely az össztömeg $\frac{18}{24}$ része. Ezek alapján felírhatjuk a következő egyenletet: $\begin{array}{c}{\displaystyle \left(60+x\right)\cdot \frac{18}{24}=25+x\mathrm{.}}\end{array}$ Rendezés és ekvivalens átalakítások után $x=80$, az ötvösnek $80$ g aranyat kell hozzáolvasztani a nyaklánchoz. 2. megoldás. Ha aranyat olvasztunk hozzá, akkor az ezüsttartalom tömege változatlanul 35 g. 18 karátos ötvözet esetén ez a teljes tömeg $\frac{6}{24}=\frac{1}{4}$ része, tehát az ötvözet tömege $35\cdot 4=140$ g. Eredetileg 60 g volt, így $140-60=80$ gramm aranyat kell hozzáolvasztani. $c)$ Az adott időszakban 20 szokásos és 5 szökőév volt, így összesen $20\cdot 365+5\cdot 366=9130$ nap telt el. Összesen a gyűrűről $\begin{array}{c}{\displaystyle \frac{0\mathrm{,}012\cdot {10}^{-3}}{197}\cdot 6\cdot {10}^{23}=3\mathrm{,}65\cdot {10}^{16}}\end{array}$ darab aranyatom vált le, amelyet a napok számával elosztva megkapjuk, hogy egyenletes kopás esetén naponta $4\cdot {10}^{12}$ (négyezer-milliárd, azaz négybillió) darab aranyatom távozott az ékszerről.   2. Egy derékszögű háromszög egyik befogójának hossza egyenlő a másik két oldalhossz számtani közepével, kerülete 276 egység. $a)$ Mekkora a háromszög köréírt körének a területe? (8 pont) $b)$ Mekkora a háromszög beírt körének a kerülete? (4 pont)   Megoldás. $a)$ A derékszögű háromszög nem egyenlő szárú, mert akkor a két befogó ugyanolyan hosszú lenne, így nem teljesülne a feladat első feltétele. Ekkor a két befogó hosszát $a$-val, illetve $b$-vel, az átfogó hosszát $c$-vel jelölve, feltehetjük, hogy $0<a<b<c$. Az első feltétel alapján felírhatjuk a következő egyenletet: $b=\frac{a+c}{2}$, amelyből $2b=a+c$. A háromszög kerülete: $K=a+b+c=276$, amelybe $a+c$ helyére $\left(2b\right)$-t helyettesítve azt kapjuk, hogy $3b=276$, azaz $b=92$ egység. $a+c=2b$ alapján $a+c=184$, amelyből kifejezzük az egyik ismeretlent: $a=184-c$. Pitagorasz tétele alapján felírhatjuk az $a^2+b^2=c^2$ egyenletet, amelybe a fentieket behelyettesítve: ${\left(184-c\right)}^2+{92}^2=c^2$, majd a zárójelet felbontva és rendezve azt kapjuk, hogy $\begin{array}{c}{\displaystyle c=\frac{{184}^2+{92}^2}{368}=115\text{egység.}}\end{array}$ A köréírt kör sugarának hossza $R=\frac{c}{2}=57\mathrm{,}5$ egység. A háromszög köréírható körének területe: $T_{\text{kör}}=R^2\pi =57\mathrm{,}{5}^2\cdot \pi \approx 10386\mathrm{,}9$ területegység. $b)$ 1. megoldás. A háromszög területe: $T=\frac{ab}{2}=3174$ területegység, félkerülete $s=\frac{K}{2}=138$ egység. Most a háromszög területére vonatkozó $T=r\cdot s$ képletből kifejezzük a háromszögbe írt kör sugarának hosszát: $\begin{array}{c}{\displaystyle r=\frac{T}{s}=\frac{3174}{138}=23\text{egység.}}\end{array}$ A háromszög beírt körének sugara $23$ egység hosszúságú. A beírt kör kerülete: $K_{\text{<span style="font-weight: normal;font-style: normal;">kör</span>}}=2r\pi =46\pi \text{<span style="font-weight: normal;font-style: normal;"> egység</span>}\approx 144\mathrm{,}5\text{<span style="font-weight: normal;font-style: normal;"> egység</span>}$. 2. megoldás. Ismert, hogy a derékszögű háromszögbe írható kör sugarának hossza kiszámítható a háromszög oldalhosszainak segítségével a következőképpen: $\begin{array}{c}{\displaystyle r=\frac{a+b-c}{2}=\frac{69+92-115}{2}=23\text{egység.}}\end{array}$ A beírt kör kerülete: $K_{\text{kör}}=2r\pi =46\pi \approx 144\mathrm{,}5\text{<span style="font-weight: normal;font-style: normal;"> egység</span>}$.   3. $a)$ Melyik az a legkisebb pozitív egész szám, amelynek négyzete osztható $504$-gyel? (3 pont) $b)$ Az első $504$ természetes szám közül véletlenszerűen kiválasztunk egyszerre négy különböző számot. Mekkora a valószínűsége, hogy legalább az egyik nagyobb $400$-nál? (5 pont) $c)$ Melyik számrendszerben írtuk fel a háromjegyű $352$ számot, ha értéke egyenlő lett a hatos számrendszerben felírt $504$ értékével? (6 pont)   Megoldás. $a)$ A szám prímtényezős felbontása: $504=2^3\cdot 3^2\cdot 7$, amelyben szerepelnek páratlan kitevők, így ez nem négyzetszám. A páratlan kitevőket a náluk nagyobb páros számok közül a legkisebbre cserélve olyan négyzetszámot kapunk, amely osztható 504-gyel, és az ilyen négyzetszámok közül a legkisebb: $2^4\cdot 3^2\cdot 7^2$. Ez a szám a $2^2\cdot 3\cdot 7=84$ négyzete. Megmutattuk, hogy a $84$ a legkisebb olyan pozitív egész szám, amelynek négyzete osztható 504-gyel. $b)$ 504 különböző elemből kiválasztunk egyszerre négyet, így összesen $\left(\genfrac{}{}{0ex}{}{504}{4}\right)$ eset van. Az első természetes számnak a nullát tekintve, az ötszáznegyedik természetes szám az 503 lesz. Ezek közül 103 darab szám nagyobb, 401 darab szám pedig nem nagyobb 400-nál. Számítsuk ki a komplementer esemény bekövetkezésének valószínűségét! Ez azt jelenti, hogy a kiválasztott számok egyike sem nagyobb 400-nál, azaz mind a négy kisebb vagy egyenlő, mint 400, így az esetek száma $\left(\genfrac{}{}{0ex}{}{401}{4}\right)$. Ekkor $\begin{array}{c}{\displaystyle p\text{'}=\frac{\left(\genfrac{}{}{0ex}{}{401}{4}\right)}{\left(\genfrac{}{}{0ex}{}{504}{4}\right)}\approx 0\mathrm{,}\mathrm{4,}}\end{array}$ ami a komplementer eseményre vonatkozik. A keresett valószínűség: $p=1-p\text{'}=0\mathrm{,}6$. $c)$ A feladat feltételei alapján felírhatjuk a következő egyenletet: ${352}_x={504}_6$, ahol $x>5$ egész szám. Az egyenlet mindkét oldalán a helyiértékek segítségével felírjuk a számjegyek valódi értékét, melyek összege az adott szám értékével egyenlő: $3\cdot x^2+5\cdot x^1+2\cdot x^0=5\cdot 6^2+0\cdot 6^1+4\cdot 6^0$, amelyből a kijelölt műveletek elvégése, majd rendezés után a $3x^2+5x-182=0$ másodfokú egyenletet kapjuk. Ennek gyökei $x_1=7$, illetve $x_2=-\frac{26}{3}$, ezek közül csak az első megoldás elégíti ki a feltételeket, tehát a kérdéses számot a hetes számrendszerben írtuk fel.   4. A KöMaL Facebook oldalán minden bejegyzésnél pontosan $2$ vagy pontosan $3$ (különböző) szerepel az előre meghatározott $10$-féle hashtagből, melyek között megtalálható a #ankét és a #kömalpóló is. Az adminisztrátorok megállapodtak, hogy amennyiben egy bejegyzésnél szerepel a #ankét, akkor szerepel a #kömalpóló is. $a)$ Hány poszt jelenhet meg októberben úgy, hogy bármely kettőben különbözzön a hashtagek halmaza, ha ősszel minden posztban szerepel a #kömalpóló? (3 pont) $b)$ Az adminisztrátorok eredeti megállapodásának betartásával hány poszt jelenhet meg úgy, hogy bármely kettőben különbözzön a hashtagek halmaza, ha más megállapodás nincs? (4 pont) $c)$ A két adminisztrátort megkérdezték, hogy összesen hányan kedvelték a szeptemberi bejegyzéseket. Az egyik így válaszolt: ,,Minden szeptemberi bejegyzést ugyanannyian lájkoltak. Ha $2$-vel kevesebb bejegyzés lett volna és mindegyiket $42$-vel többen kedvelték volna, akkor $744$-gyel több lájkot gyűjtöttünk volna.'' A másik adminisztrátor válasza így hangzott: ,,Ha $3$-mal többször posztoltunk volna, de mindegyiket félszázzal kevesebben kedvelték volna, akkor $976$-tal kevesebb lájkunk lett volna.'' Összesen hány lájkot gyűjtöttek szeptemberben? (6 pont)   Megoldás. $a)$ A #kömalpóló mellé a másik 9 darab hashtagből kell választani még egyet, illetve kettőt, így összesen $\left(\genfrac{}{}{0ex}{}{9}{1}\right)+\left(\genfrac{}{}{0ex}{}{9}{2}\right)=9+36=45$ különböző eset van, így legfeljebb 45 poszt jelenhet meg októberben, amely megfelel a feltételeknek. $b)$ 1. eset. Ha szerepel a #ankét, akkor a #kömalpóló is ott van, ezért a maradék 8 hashtagből már nem kell egy sem, vagy egy kell közülük, így ekkor $\left(\genfrac{}{}{0ex}{}{8}{0}\right)+\left(\genfrac{}{}{0ex}{}{8}{1}\right)=1+8=9$ különböző eset van. 2. eset. Ha nem szerepel a #ankét, akkor a másik 9 darab hashtagből kell mindkettőt, illetve mindhármat kiválasztani, ezért ekkor $\left(\genfrac{}{}{0ex}{}{9}{2}\right)+\left(\genfrac{}{}{0ex}{}{9}{3}\right)=36+84=120$ különböző eset van. Összesen $9+120=129$ poszt jelenhet meg úgy, hogy bármely kettőben különbözzön a hashtagek halmaza, ha más megállapodás nincs. $c)$ A szeptemberi bejegyzések számát $x$-szel, az egy-egy bejegyzést kedvelők számát $y$-nal jelölve, a szeptemberi kedvelések száma összesen $x\cdot y$, ekkor a feladatban megadott adatok alapján felírhatjuk a következő egyenletrendszert: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left(x-2\right)\left(y+42\right)}& {\displaystyle =x\cdot y+\mathrm{744,}}\hfill \\ \hfill {\displaystyle \left(x+3\right)\left(y-50\right)}& {\displaystyle =x\cdot y-\mathrm{976,}}\hfill \end{array}}$ amelyből a műveletek elvégzése és rendezés után azt kapjuk, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 42x-2y}& {\displaystyle =\mathrm{828,}}\hfill \\ \hfill {\displaystyle -50x+3y}& {\displaystyle =-826.}\hfill \end{array}}$ Ezt többféleképpen megoldhatjuk, például az egyenlő együtthatók módszerével úgy, hogy az első egyenletet 3-mal, a másodikat 2-vel megszorozzuk, majd a kapott egyenleteket összeadva a $26x=832$ egyenlethez jutunk. Ebből $x=32$, amelyet behelyettesítve az eredeti egyenletek bármelyikébe, kiszámoljuk, hogy $y=258$. Szeptemberben összesen $32\cdot 258=8256$ lájkot kaptak. Ellenőrzés: Ha $32-2=30$ bejegyzés lett volna, és minden bejegyzésre $258+42=300$ kedvelés érkezett volna, akkor $30\cdot 300=9000$ lájk gyűlt volna össze, ami valóban 744-gyel több, mint a 8256. Ha pedig $32+3=35$ bejegyzés lett volna, és mindegyiket $258-50=208$ fő lájkolta volna, akkor $35\cdot 208=7280$ lájk jött volna összesen, ami tényleg 976-tal kevesebb, mint a 8256.   II. rész     5. Adott a $k$ kör, amelynek egyenlete $x^2+y^2=20x-21y$ és a $P(-\frac{1}{2};p)$ pont, ahol $p$ valós paraméter. $a)$ Határozzuk meg a $p$ valós paraméter összes értékét, amelyre $P$ a $k$ körön kívül helyezkedik el. (5 pont) Legyen az $AB$ szakasz a $k$ kör azon átmérője, amelyre illeszkedik a $Q\left(5;-5\mathrm{,}25\right)$ pont. $b)$ Számítsuk ki az $A$ és a $B$ pont koordinátáit! (5 pont) A $k$ körön belül véletlenszerűen rábökünk egy pontra. $c)$ Adjuk meg annak a valószínűségét, hogy a kiválasztott pont nincs messzebb a $k$ kör középpontjától, mint a $Q$ pont! (6 pont)   Megoldás. $a)$ Az egyenlet valóban egy kör egyenlete. Ezt az egyenlet teljes négyzetté alakításával igazolhatjuk: $\begin{array}{c}{\displaystyle {\left(x-10\right)}^2+{\left(y+\frac{21}{2}\right)}^2=\frac{841}{4}\mathrm{.}}\end{array}$ A $P$ pont akkor és csak akkor van a körön kívül, ha a kör középpontjától mért távolsága nagyobb, mint a kör sugara, azaz koordinátái kielégítik az alábbi egyenlőtlenséget: $\begin{array}{c}{\displaystyle {\left(x-10\right)}^2+{\left(y+\frac{21}{2}\right)}^2>\frac{841}{4}\mathrm{.}}\end{array}$ Ezt átrendezve az $x^2+y^2>20x-21y$ egyenlőtlenséghez jutunk. A $P$ pont koordinátáit behelyettesítjük az egyenlőtlenség megfelelő változóinak helyére: $\begin{array}{c}{\displaystyle {\left(-\frac{1}{2}\right)}^2+p^2>20\cdot \left(-\frac{1}{2}\right)-21p\mathrm{,}}\end{array}$ majd elvégezzük a kijelölt műveleteket és nullára redukálunk: $\begin{array}{c}{\displaystyle p^2+21p+\frac{41}{4}>0.}\end{array}$ A kapott egyenlőtlenség megoldása: $p<-\frac{41}{2}$ vagy $p>-\frac{1}{2}$, ezen értékek megfelelnek a feltételeknek, így a megoldáshalmaz a következő: $\begin{array}{c}{\displaystyle p\in \left]-\infty ;-\frac{41}{2}\right[\cup \left]-\frac{1}{2};\infty \right[\mathrm{.}}\end{array}$ $b)$ A kör középpontja illeszkedik az átmérőre, ezért a kör középponti egyenletéből kiolvassuk a $K$ középpont koordinátáit és a sugár hosszát: $K(10;-\frac{21}{2})$, $\begin{array}{c}{\displaystyle r=\sqrt[]{\frac{841}{4}}=\frac{29}{2}\text{egység.}}\end{array}$ Az $AB$ átmérőre illeszkedik a $Q$ és a $K$ pont is, így egyenesének egyenlete felírható a két pont koordinátáinak segítségével: $\begin{array}{c}{\displaystyle d:\left(10-5\right)\left(y-\left(-5\mathrm{,}25\right)\right)=\left(-10\mathrm{,}5-\left(-5\mathrm{,}25\right)\right)\left(x-5\right)\mathrm{,}}\end{array}$ amelyből ekvivalens átalakítások után a  $d:y=-\frac{21}{20}x$ egyenletet kapjuk. Az $A$ és a $B$ pont egyaránt illeszkedik a $k$ körre és a $d$ egyenesre, így koordinátáikat az alábbi egyenletrendszer megoldásaiként kapjuk meg: ${\displaystyle \begin{array}{c}\hfill {\displaystyle x^2+y^2=20x-21y\mathrm{,}}\hfill \\ \hfill {\displaystyle y=-\frac{21}{20}x\mathrm{.}}\hfill \end{array}}$ Az első egyenletben $y$ helyett $(-\frac{21}{20}x)$-et írva, majd rendezve, a $\begin{array}{c}{\displaystyle \frac{841}{400}{x}^2-\frac{841}{20}x=0}\end{array}$ hiányos másodfokú egyenlethez jutunk, amelyet szorzattá alakítva az $x_1=0$ és $x_2=20$ gyököket kapjuk. A kapott értékeket visszahelyettesítve a második egyenletbe: $y_1=0$ és $y_2=21$, így a keresett két pont az $A\left(0;0\right)$ és a $B\left(20;-21\right)$. $c)$ A keresett valószínűség megegyezik a $K$ középpontú, $KQ$ sugarú kör területének és a $k$ kör területének hányadosával, ami éppen a megfelelő sugárhosszak arányának négyzetével egyenlő: $r_k=14\mathrm{,}5$ egység, $|KQ|=\sqrt[]{5^2+5\mathrm{,}{25}^2}=7\mathrm{,}25$ egység, $\begin{array}{c}{\displaystyle p={\left(\frac{7\mathrm{,}25}{14\mathrm{,}5}\right)}^2=\frac{1}{4}\mathrm{.}}\end{array}$   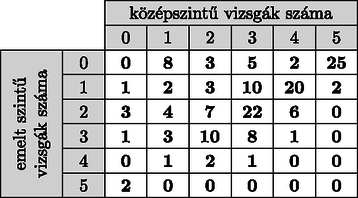6. Nevesincs szigeten felmérést végeztek az idén érettségiző $152$ diák megkérdezésével. Az első kérdés arra vonatkozott, hogy ki hány tárgyból vizsgázik közép-, illetve emelt szinten. A válaszokat az alábbi táblázat mutatja:     Például $20$ olyan diák van, aki $4$ tárgyból középszintű, $1$ tárgyból pedig emelt szintű vizsgára jelentkezett, ugyanakkor $5$ tanuló $3$ tárgyból középszinten vizsgázik, emelt szintű vizsgát pedig idén nem tesz. $a)$ Összesen hány emelt szintű vizsgát terveznek a diákok? (3 pont) $b)$ Hányan érettségiznek pontosan $5$ tárgyból? (3 pont) $c)$ Határozzuk meg a legfeljebb $4$ tárgyból vizsgázók között a középszintű vizsgák számának leggyakoribb értékét, illetve mediánját! (5 pont) $d)$ Számítsuk ki az egy főre jutó átlagos vizsgaszámot! (5 pont)   Megoldás. $a)$ Az emelt szintű vizsgák száma: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle 0\cdot \left(8+3+5+2+25\right)+1\cdot \left(1+2+3+10+20+2\right)+2\cdot \left(3+4+7+22+6\right)+}\hfill \\ \hfill {\displaystyle }& {\displaystyle +3\cdot \left(1+3+10+8+1\right)+4\cdot \left(1+2+1\right)+5\cdot 2=0+38+84+69+16+10=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =217\text{darab.}}\hfill \end{array}}$ $b)$ Pontosan 5 tárgyból vizsgázik, aki $•$ 5 középszintű vizsgát tesz, és nem vizsgázik emelt szinten (a táblázat utolsó oszlopának a legfelső sorában szerepel): 25 fő, $•$ 4 középszintű és 1 emelt szintű vizsgát tesz (utolsó előtti oszlop második sorában): 20 fő, $•$ 3 középszintű és 2 emelt szintű vizsgát tesz (negyedik oszlop harmadik sorában): 22 fő, $•$ 2 középszintű és 3 emelt szintű vizsgát tesz (harmadik oszlop negyedik sorában): 10 fő, $•$ 1 középszintű és 4 emelt szintű vizsgát tesz (második oszlop ötödik sorában): 1 fő, $•$ 5 emelt szintű vizsgát tesz, és nem tesz középszintű érettségit (első oszlop utolsó sorában): 2 fő. Összesen: 80 fő tesz pontosan öt tárgyból érettségit idén. $c)$ A legfeljebb négy tantárgyból vizsgázók a táblázatban éppen a $b)$ részben szereplő (pontosan 5 tantárgyból vizsgázók) fölött vannak, tehát az 1. oszlop felső 5 sorában, a 2. oszlop felső 4 sorában, és így tovább, mindig 1-gyel kevesebb sorban, amíg eljutunk az uolsó oszlopba, ahol nincs ilyen tanuló. Oszloponként összeadva a létszámot, megkapjuk, hogy középszinten hányan tesznek egy adott számú vizsgát. Táblázatba foglalva:   ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{középszintű vizsgák száma }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4}}\hfill \\ \hfill {\displaystyle \text{vizsgázók száma (a legfeljebb 4 tárgyból vizsgázók közül) }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 17 }}\hfill & \hfill {\displaystyle \text{ 13 }}\hfill & \hfill {\displaystyle \text{ 15 }}\hfill & \hfill {\displaystyle \text{ 2}}\hfill \\ \hline\end{array}}$   Az így kapott adathalmaz módusza az 1, mediánja pedig a 2, tehát a legfeljebb 4 tárgyból vizsgázók között a középszintű vizsgák számának leggyakoribb értéke az 1 (darab) vizsga, mediánja pedig a 2 (darab) vizsga. $d)$ Az egy főre jutó átlagos vizsgaszámot úgy számítjuk ki, hogy a vizsgák számát elosztjuk a létszámmal. A $b)$ feladatrészben láttuk, hogy a pontosan egy adott számú vizsgát tevő diákok a táblázatban átlósan találhatóak, így összeadjuk a számokat és megszorozzuk a vizsgák számával. Az így kapott szorzatokat összeadva kapjuk a vizsgák számát: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 7\cdot \left(1+1\right)+6\cdot \left(2+6+8+2\right)+5\cdot 80+4\cdot \left(2+10+7+3+0\right)+}\hfill \\ \hfill {\displaystyle +3\cdot \left(5+3+4+1\right)+2\cdot \left(3+2+3\right)+1\cdot \left(8+1\right)=674.}\hfill \end{array}}$ Átlagosan $\frac{674}{152}=4\mathrm{,}43$ darab vizsgát tesznek fejenként a tanulók.     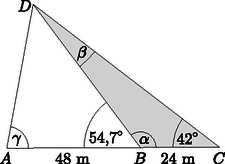7. Olaszországi kirándulása során Zéta méréssel meghatározta a pisai ferde torony épületének hosszát. A torony talpától először kimért 48 métert abba az irányba, amerre a torony dől, és innen a torony teteje 54,7 fokos szögben látszott. Ezután ugyanabban az irányban még 24 métert ment, ahonnan a torony teteje már csak 42 fokos szögben látszott.     $a)$ Határozzuk meg a torony hosszát Zéta mérési eredményei alapján, majd adjuk meg annak százalékos eltérését a torony valódi hosszúságától, amely 56,3 méter. (6 pont) $b)$ Mekkora szöget zár be az épület a vízszintes talajjal? (3 pont) $c)$ Zéta öccse, Zétény felment a toronyba és közben megszámolta a lépcsőket. Felérve megállapította, hogy a lépcsőfokok száma egy olyan mértani sorozat harmadik eleme, amelyhez hozzáadva a második elemet 336-ot kapunk összegként. Ugyanezen sorozat ötödik eleméből kivonva a harmadik elemet, a különbség $14112$. Hány lépcsőfok van a pisai ferde toronyban? (7 pont)   Megoldás. $a)$ Az ábra jelöléseit használva: $\begin{array}{c}{\displaystyle \alpha ={180}^{\circ }-54\mathrm{,}{7}^{\circ }=125\mathrm{,}{3}^{\circ }\text{és}\beta ={180}^{\circ }-125\mathrm{,}{3}^{\circ }-{42}^{\circ }=12\mathrm{,}{7}^{\circ }\mathrm{.}}\end{array}$     A $BCD$ háromszögben alkalmazva a szinusztételt, felírhatjuk a $\begin{array}{c}{\displaystyle \frac{24}{\text{sin}{12\mathrm{,}7}^{\circ }}=\frac{BD}{\text{sin}{42}^{\circ }}}\end{array}$ egyenletet, amelyből $BD\approx 73$ méter. Most alkalmazzuk a koszinusztételt az $ABD$ háromszögben az $AD$ oldalhossz meghatározására: $A{D}^2={48}^2+{73}^2-2\cdot 48\cdot 73\cdot \text{cos}54\mathrm{,}{7}^{\circ }=3583\mathrm{,}37$, ebből $AD\approx 59\mathrm{,}9$ méter. $\frac{59\mathrm{,}9}{56\mathrm{,}3}\approx 1\mathrm{,}064$, tehát a mérések alapján meghatározott érték 6,4%-kal nagyobb a torony valódi hosszánál. $b)$ A koszinusztételt felhasználhatjuk az $ABD$ háromszögben a dőlésszög nagyságának meghatározására is: $\begin{array}{c}{\displaystyle \text{cos}\gamma =\frac{59\mathrm{,}{9}^2+{48}^2-{73}^2}{2\cdot 59\mathrm{,}9\cdot 48}\mathrm{,}\text{így}\gamma \approx 84\mathrm{,}{4}^{\circ }\mathrm{.}}\end{array}$ A torony a vízszintes talajjal hozzávetőlegesen $84\mathrm{,}{4}^{\circ }$ nagyságú szöget zár be. $c)$ Legyen $q\left(\ne 0\right)$ a mértani sorozat hányadosa, $a_n\left(\ne 0\right)$ pedig a sorozat $n$-edik tagja. Ekkor a feladat szövege alapján felírhatjuk a következő egyenletrendszert: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_3+a_2}& {\displaystyle =\mathrm{336,}}\hfill \\ \hfill {\displaystyle a_5-a_3}& {\displaystyle =14112.}\hfill \end{array}}$ Az első egyenletben két egymást követő tag pozitív összeget ad, így a hányados nem lehet $-1$ sem. Az $a_n=a_1\cdot q^{n-1}$ képlet többszöri alkalmazásával átalakítjuk az egyenletrendszert:   ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_1\cdot q^2+a_1\cdot q}& {\displaystyle =\mathrm{336,}}\hfill \\ \hfill {\displaystyle a_1\cdot q^4-a_1\cdot q^2}& {\displaystyle =14112.}\hfill \end{array}}$ Az első egyenletből $\left(a_1\cdot q\right)$-t, a másodikból $\left(a_1\cdot q^2\right)$-t kiemelve, majd a megfelelő (nemnulla) oldalakat elosztva egymással, a bal oldalon $\left(a_1\cdot q\right)$-val, míg a jobb oldalon $336$-tal egyszerűsítünk: $\frac{q\left(q^2-1\right)}{q+1}=42$, ahol $q\ne -1$. Tudjuk, hogy $q^2-1=\left(q-1\right)\left(q+1\right)$, így $\left(q+1\right)$-gyel is egyszerűsíthetünk, így a $q\left(q-1\right)=42$ egyenlethez jutunk, amelynek gyökei $q_1=7$ és $q_2=-6$. A kapott értékeket az $a_1\cdot q^2+a_1\cdot q=336$ egyenletbe helyettesítve $a_{1_1}=6$ és $a_{1_2}=11\mathrm{,}2$, ebből $a_{3_1}=6\cdot 7^2=294$, ugyanakkor $a_{3_2}=11\mathrm{,}2\cdot {\left(-6\right)}^2=403\mathrm{,}2$, az utóbbi nem egész szám, ezért nem felel meg a feladat feltételeinek. A pisai ferde toronyban 294 lépcső van.   8. Adott a valós számok lehető legbővebb részhalmazán értelmezett $\begin{array}{c}{\displaystyle f\left(x\right)=\text{log}{}_{\frac{1}{3}}x\text{és}g\left(x\right)=3x+1}\end{array}$ függvény. $a)$ Írjuk fel az $u=f\circ g$ és a $v=g\circ f$ függvények hozzárendelési szabályát, határozzuk meg értelmezési tartományukat és értékkészletüket. (8 pont) $b)$ Adjuk meg az $f\left(x\right)$, illetve a $g\left(x\right)$ függvény egy-egy olyan leszűkítését, amelynek értékkészlete $•$ $\left]-3;5\right]$; $•$ a természetes számok halmaza; $•$ a racionális számok halmaza. (8 pont)   Megoldás. $a)$ $u\left(x\right)=f\left(g\left(x\right)\right)=\text{log}{}_{\frac{1}{3}}\left(3x+1\right)$, ahol $3x+1>0$, $x>-\frac{1}{3}$, ezért $D_u=]-\frac{1}{3};\infty [$, $R_u=\text{R}$. $v\left(x\right)=g\left(f\left(x\right)\right)=3\cdot \text{log}{}_{\frac{1}{3}}\left(x\right)+1$, ahol $x>0$, ezért $D_v=\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>R</mi></mrow><mrow><mo stretchy="false">+</mo></mrow></msup></mrow></math>}$, $R_v=\text{R}$. $b)$ Az $f\left(x\right)$ függvény folytonossága és szigorú monoton csökkenése miatt elegendő a megadott értékkészlet végpontjainak megfelelően vizsgálatokat végezni, azaz megoldani a következő két egyenlőtlenséget: $\text{log}{}_{\frac{1}{3}}x>-3$, amelyből $x<27$; illetve $\text{log}{}_{\frac{1}{3}}x\le 5$, amelyből $x\ge \frac{1}{243}$, így a megfelelő leszűkítés a következő: $\begin{array}{c}{\displaystyle f{\left(x\right)}_1:\left[\frac{1}{243};27\right[\to \left]-3;5\right]\mathrm{.}}\end{array}$ A másik két leszűkítésnél a logaritmus alapjának megfelelő hatványai alkotják az értelmezési tartományt, így a kérdezett leszűkítések rendre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle f{\left(x\right)}_2}& {\displaystyle :\left\{x|x={\left(\frac{1}{3}\right)}^n;n\in \text{N}\right\}\to \text{N};\text{illetve}}\hfill \\ \hfill {\displaystyle f{\left(x\right)}_3}& {\displaystyle :\left\{x|x={\left(\frac{1}{3}\right)}^q;q\in \text{Q}\right\}\to \text{Q}\mathrm{.}}\hfill \end{array}}$ A $g\left(x\right)$ függvény leszűkítéseit a fentiekhez hasonlóan határozhatjuk meg. Ezek rendre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle g{\left(x\right)}_1}& {\displaystyle :\left]-\frac{4}{3};\frac{4}{3}\right]\to \left]-3;5\right];}\hfill \\ \hfill {\displaystyle g{\left(x\right)}_2}& {\displaystyle :\left\{x|x=\frac{1}{3}\left(n-1\right);n\in \text{N}\right\}\to \text{N};\text{illetve}g{\left(x\right)}_3:\text{Q}\to \text{Q}\mathrm{.}}\hfill \end{array}}$   9. Egy 7 dm hosszúságú szakaszt felosztunk két részre. $a)$ Bizonyítsuk be, hogy az így kapott egyik szakaszhossz köbének és a másik szakaszhossz négyzetének szorzata akkor a legnagyobb, ha az egyik szakasz hossza 42 cm. (8 pont) $b)$ Hány olyan különböző háromszög van, amelynek két oldala az $a)$ részben kapott két szakasz, és a harmadik oldalának hossza is centiméterben mérve egész szám? (3 pont) $c)$ Mekkora lehet a legnagyobb belső szöge annak a háromszögnek a fentiek közül, amelynek oldalhosszai számtani sorozatot alkotnak? (5 pont)   Megoldás. $a)$ Legyen az eredeti szakasz egyik részének hossza $x$ cm ($0<x<70)$, ekkor a másik rész hossza $70-x$ cm. Keressük az $f\left(x\right)=x^3\cdot {\left(70-x\right)}^2$ függvény lokális maximumát az adott intervallumon. $\begin{array}{c}{\displaystyle f\left(x\right)=x^5-140x^4+4900x^3\mathrm{,}}\end{array}$ ennek deriváltfüggvénye $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=5x^4-560x^3+14700x^2\mathrm{.}}\end{array}$ A függvénynek ott lehet lokális szélsőértéke, ahol a deriváltja nulla: $5x^4-560x^3+14700x^2=0$. A kapott egyenlet mindkét oldalát elosztva az $x^2$ pozitív értékű kifejezéssel másodfokú egyenletet kapunk: $5x^2-560x+14700=0$, amelynek gyökei $x_1=70$ és $x_2=42$. Az első megoldás nem eleme az értelmezési tartománynak, a második megoldás eleme. Ellenőrizzük, hogy $x=42$-nél valóban lokális maximuma van a függvénynek. Ezt többféleképpen is megtehetjük, például a második derivált segítségével: $\begin{array}{c}{\displaystyle f\text{'}\text{'}\left(42\right)=20\cdot {42}^3-1680\cdot {42}^2+29400\cdot 42=-246\mathrm{960,}}\end{array}$ azaz itt a második deriváltfüggvény értéke negatív, tehát valóban lokális maximumhelyet találtunk, így a feladat állítását beláttuk. $b)$ A háromszög két oldalának hossza $28$ és $42$ cm, a harmadiké legyen $z$ cm $\left(z\in {\text{Z}}^{+}\right)$. A háromszög-egyenlőtlenséget alkalmazva: $28+z>42$ és $42+28>z$, amiből $14<z<70$. 55 ilyen egész szám van, tehát 55 különböző háromszög létezik, amely megfelel a feltételeknek. $c)$ Három esetet kell megvizsgálnunk aszerint, hogy $z$ oldal 1) a legrövidebb, 2) a leghosszabb, vagy 3) 28 és 42 cm között van. 1. eset. $z;28;42$ számtani sorozat egymást követő elemeiként igaz, hogy $28=\frac{z+42}{2}$; ebből $z=14$, ami a háromszög-egyenlőtlenség miatt nem lehet, így nincs ilyen háromszög. 2. eset. $28;42;z$, ekkor $42=\frac{28+z}{2}$; ebből $z=56$ cm. A háromszög oldalai 28; 42 és 56 centiméteresek, a legnagyobb belső szög a leghosszabb oldallal szemben fekszik. A koszinusztételt alkalmazva, a keresett szöget $\phi$-vel jelölve: $\begin{array}{c}{\displaystyle \text{cos}\phi =\frac{{28}^2+{42}^2-{56}^2}{2\cdot 28\cdot 42}=-\frac{1}{4};\phi \approx 104\mathrm{,}{5}^{\circ }\mathrm{.}}\end{array}$ 3. eset. $28;z;42$, ekkor $z=\frac{28+42}{2}=35$ cm, így a legnagyobb belső szög a 42 centiméteres oldallal szemközt található, jelöljük $\omega$-val. A 2. esetben látott módon meghatározzuk $\omega$ nagyságát, $\begin{array}{c}{\displaystyle \omega =\frac{{28}^2+{35}^2-{42}^2}{2\cdot 28\cdot 35}=\frac{1}{8};\omega \approx 82\mathrm{,}{8}^{\circ }\mathrm{.}}\end{array}$ A feltételeknek megfelelő háromszög legnagyobb belső szögének nagysága $82\mathrm{,}{8}^{\circ }$ vagy $104\mathrm{,}{5}^{\circ }$ lehet.