Kezdőlap


Cím:	Gyakorló feladatsor emelt szintű matematikai érettségire
Szerző(k):	Kozma Katalin Abigél, Győr
Füzet:	2021/október, 392 - 395. oldal	PDF \| MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az első néhány számban a feladatsorok nem fedik le teljes egészében a hivatalos követelményrendszert, hogy a már tanult ismereteket kelljen csak felhasználni a megoldáshoz. Igyekszünk a feladatsorok nehézségét az éles sorokhoz igazítani, vagyis ‐ az előző évekhez képest ‐ könnyebbek lesznek.

I. rész

1. A karát egy viszonyszám, amely megmutatja, hogy mekkora az aranyötvözetben az arany tömegaránya.

a)

Hány gramm ezüstöt tartalmaz egy 10 karátos 0,06 kg tömegű nyaklánc, amely csak aranyat és ezüstöt tartalmaz, ha a színarany 24 karátos?

(2 pont)

b)

Hány gramm aranyat olvasszon a nyaklánchoz az ötvös, ha 18 karátos ötvözetet szeretne létrehozni?

(4 pont)

c)

Az ötvösmester pontosan 25 éve hordja az egyik aranygyűrűjét, és megállapította, hogy időközben a gyűrű aranytartalmának tömege 0,012 milligrammal csökkent. Számítsuk ki, hogy naponta hány aranyatom vált le a gyűrűről, ha 197 gramm arany hozzávetőlegesen

6 \cdot 10^{23}

darab aranyatomot tartalmaz. (Feltételezzük, hogy a kopás egyenletesen ment végbe, és tudjuk, hogy ezen időszakban 5 szökőév volt.)

(6 pont)

2. Egy derékszögű háromszög egyik befogójának hossza egyenlő a másik két oldalhossz számtani közepével, kerülete 276 egység.

a)

Mekkora a háromszög köréírt körének a területe?

(8 pont)

b)

Mekkora a háromszög beírt körének a kerülete?

(4 pont)

a)

Melyik az a legkisebb pozitív egész szám, amelynek négyzete osztható 504-gyel?

(3 pont)

b)

Az első 504 természetes szám közül véletlenszerűen kiválasztunk egyszerre négy különböző számot. Mekkora a valószínűsége, hogy legalább az egyik nagyobb 400-nál?

(5 pont)

c)

Melyik számrendszerben írtuk fel a háromjegyű 352 számot, ha értéke egyenlő lett a hatos számrendszerben felírt 504 értékével?

(6 pont)

4. A KöMaL Facebook oldalán minden bejegyzésnél pontosan 2 vagy pontosan 3 (különböző) szerepel az előre meghatározott 10-féle hashtagből, melyek között megtalálható a #ankét és a #kömalpóló is. Az adminisztrátorok megállapodtak, hogy amennyiben egy bejegyzésnél szerepel a #ankét, akkor szerepel a #kömalpóló is.

a)

Hány poszt jelenhet meg októberben úgy, hogy bármely kettőben különbözzön a hashtagek halmaza, ha ősszel minden posztban szerepel a #kömalpóló?
(3 pont)

b)

Az adminisztrátorok eredeti megállapodásának betartásával hány poszt jelenhet meg úgy, hogy bármely kettőben különbözzön a hashtagek halmaza, ha más megállapodás nincs?

(4 pont)

c)

A két adminisztrátort megkérdezték, hogy összesen hányan kedvelték a szeptemberi bejegyzéseket. Az egyik így válaszolt: ,,Minden szeptemberi bejegyzést ugyanannyian lájkoltak. Ha 2-vel kevesebb bejegyzés lett volna és mindegyiket 42-vel többen kedvelték volna, akkor 744-gyel több lájkot gyűjtöttünk volna.'' A másik adminisztrátor válasza így hangzott: ,,Ha 3-mal többször posztoltunk volna, de mindegyiket félszázzal kevesebben kedvelték volna, akkor 976-tal kevesebb lájkunk lett volna.'' Összesen hány lájkot gyűjtöttek szeptemberben?

(6 pont)

II. rész

5. Adott a

k

kör, amelynek egyenlete

x^{2} + y^{2} = 20 x - 21 y

és a

P (- \frac{1}{2}; p)

pont, ahol

p

valós paraméter.

a)

Határozzuk meg a

p

valós paraméter összes értékét, amelyre

P

k

körön kívül helyezkedik el.

(5 pont)

Legyen az

A B

szakasz a

k

kör azon átmérője, amelyre illeszkedik a

Q (5; - 5, 25)

pont.

b)

Számítsuk ki az

A

és a

B

pont koordinátáit!

(5 pont)

k

körön belül véletlenszerűen rábökünk egy pontra.

c)

Adjuk meg annak a valószínűségét, hogy a kiválasztott pont nincs messzebb a

k

kör középpontjától, mint a

Q

pont!

(6 pont)

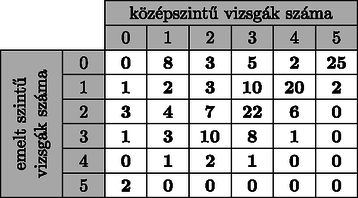
6. Nevesincs szigeten felmérést végeztek az idén érettségiző 152 diák megkérdezésével. Az első kérdés arra vonatkozott, hogy ki hány tárgyból vizsgázik közép-, illetve emelt szinten. A válaszokat az alábbi táblázat mutatja:

Például 20 olyan diák van, aki 4 tárgyból középszintű, 1 tárgyból pedig emelt szintű vizsgára jelentkezett, ugyanakkor 5 tanuló 3 tárgyból középszinten vizsgázik, emelt szintű vizsgát pedig idén nem tesz.

a)

Összesen hány emelt szintű vizsgát terveznek a diákok?

(3 pont)

b)

Hányan érettségiznek pontosan 5 tárgyból?

(3 pont)

c)

Határozzuk meg a legfeljebb 4 tárgyból vizsgázók között a középszintű vizsgák számának leggyakoribb értékét, illetve mediánját!

(5 pont)

d)

Számítsuk ki az egy főre jutó átlagos vizsgaszámot!

(5 pont)

7. Olaszországi kirándulása során Zéta méréssel meghatározta a pisai ferde torony épületének hosszát. A torony talpától először kimért 48 métert abba az irányba, amerre a torony dől, és innen a torony teteje 54,7 fokos szögben látszott. Ezután ugyanabban az irányban még 24 métert ment, ahonnan a torony teteje már csak 42 fokos szögben látszott.

a)

Határozzuk meg a torony hosszát Zéta mérési eredményei alapján, majd adjuk meg annak százalékos eltérését a torony valódi hosszúságától, amely 56,3 méter.

(6 pont)

b)

Mekkora szöget zár be az épület a vízszintes talajjal?

(3 pont)

c)

Zéta öccse, Zétény felment a toronyba és közben megszámolta a lépcsőket. Felérve megállapította, hogy a lépcsőfokok száma egy olyan mértani sorozat harmadik eleme, amelyhez hozzáadva a második elemet 336-ot kapunk összegként. Ugyanezen sorozat ötödik eleméből kivonva a harmadik elemet, a különbség

14 112

. Hány lépcsőfok van a pisai ferde toronyban?

(7 pont)

8. Adott a valós számok lehető legbővebb részhalmazán értelmezett

\begin{matrix} f (x) = log_{\frac{1}{3}} x és g (x) = 3 x + 1 \end{matrix}

függvény.

a)

Írjuk fel az

u = f \circ g

és a

v = g \circ f

függvények hozzárendelési szabályát, határozzuk meg értelmezési tartományukat és értékkészletüket.

(8 pont)

b)

Adjuk meg az

f (x)

, illetve a

g (x)

függvény egy-egy olyan leszűkítését, amelynek értékkészlete

$•$	$] - 3; 5]$ ;

$•$	a természetes számok halmaza;

$•$	a racionális számok halmaza.

(8 pont)

9. Egy 7 dm hosszúságú szakaszt felosztunk két részre.

a)

Bizonyítsuk be, hogy az így kapott egyik szakaszhossz köbének és a másik szakaszhossz négyzetének szorzata akkor a legnagyobb, ha az egyik szakasz hossza 42 cm.

(8 pont)

b)

Hány olyan különböző háromszög van, amelynek két oldala az

a)

részben kapott két szakasz, és a harmadik oldalának hossza is centiméterben mérve egész szám?

(3 pont)

c)

Mekkora lehet a legnagyobb belső szöge annak a háromszögnek a fentiek közül, amelynek oldalhosszai számtani sorozatot alkotnak?

(5 pont)