Cím:	Gyakorló feladatsor emelt szintű matematika érettségire
Szerző(k):	Kozma Katalin Abigél, Győr
Füzet:	2021/január, 16 - 19. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor, Matematika

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Az $f$ függvény olyan, hogy minden $x\in \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>R</mi></mrow><mrow><mo stretchy="false">+</mo></mrow></msup></mrow></math>}$-re $f\left(x\right)=\sqrt[]{2+\sqrt[]{\text{log}{}_2^{2}x}}$. Hol veszi fel a függvény a 2 értéket? (6 pont) $b)$ Adott egy $g$ függvény úgy, hogy minden $x\in D_g$-re $g\left(x+1\right)=\frac{2g\left(x\right)+1}{2}$ és $g\left(2021\right)=2021$. Mennyi $g\left(2020\right)$? (4 pont)   2. $a)$ Huba a bolhapiacon szeretné eladni az okostelefonját. Tapasztalatból tudja, hogy az ár $\frac{1}{5}$ részét lealkudják a vásárlók, ezért a megállapított érték $\frac{1}{4}$ részével többet kér, így az alku után éppen annyit kap, amennyit szeretne. Ezúttal azonban a telefon értékének 90%-ával tért haza. Hányadrészét kapta meg Huba a telefon piacon kihirdetett árának? (5 pont) $b)$ Vacsora után Huba $n=1$-től $100$-ig sorban felírta az $n$ után következő pozitív egész szám négyzetének és $n$ négyzetének a különbségét. Testvére, Luca meglátta a számsort és elölről kezdve bekarikázott 24 prímszámot. Meglepve látta, hogy az utolsó bekarikázott szám a sorban éppen annyiadik helyen áll, ahány gyertya volt aznap édesanyja születésnapi tortáján. Hány éves Huba anyukája? (8 pont)   3. $a)$ Mennyi az alábbi táblázatban szereplő számok összege? (8 pont)     $b)$ Hétfőn Gabi vett néhány részvényt, másnap 10 százalékot veszítettek értékükből, ám szerdán nőtt az értékük 10 százalékkal. Ez így folytatódott azon a héten és még a következő héten is. Hogyan változott Gabi részvényeinek értéke a második hét utolsó napjára? (5 pont)   4. Adott az $A\left(2020;2021\right)$, $B\left(2027;2025\right)$, $C\left(2022;2027\right)$ és a $D\left(2026;2022\right)$ pont a Descartes-féle koordinátarendszerben. Legyen az $E$ pont az $AB$ és a $CD$ szakasz metszéspontja. $a)$ Határozzuk meg az $AE$ és az $EB$ szakaszhosszak arányát. (7 pont) $b)$ Számítsuk ki a négy adott pont által meghatározott négyszög kerületét és területét. (8 pont)   II. rész     5. $a)$ Az $A$ halmaz az $a{x}^2-bx+c=0$ egyenlet $(a\mathrm{,}b\mathrm{,}c\in \text{R}\setminus \left\{0\right\}$ és $b^2-4ac\ge 0)$ összes valós gyökének reciprokát tartalmazza. Fejezzük ki az $A$ halmaz elemeinek összegét az $a$, $b$, $c$ paraméterek segítségével. (6 pont) $b)$ Öten beszélgetnek a pozitív egész számokat tartalmazó $B$ halmazról. Tudják, hogy $B$-ben van legalább egy olyan elem, ami nagyobb 1-nél és ha a $B$ halmaz tartalmaz egy $n$ számot, akkor az összes $n$-nél nagyobb számot is tartalmazza, kivéve esetleg az $n$ néhány többszörösét. A következő állítások hangzanak el a beszélgetés során: Andi: ,,$B$ számossága véges.'' Bulcsú: ,,Végtelen sok olyan pozitív egész szám van, ami nincs benne $B$-ben, és végtelen sok olyan, ami benne van.'' Cecília: ,,Szerintem az összes pozitív prímszám benne van a $B$ halmazban.'' Dani: ,,$B={\text{Z}}^{+}$.'' Emőke: ,,Létezik egy olyan $m$ pozitív egész szám, hogy $B$ tartalmazza az összes $m$-nél nagyobb egész számot.'' Ki(k)nek van biztosan igaza? Indokoljuk válaszunkat. (6 pont) $c)$ Később az intervallumok is szóba kerülnek. Adott két valós szám: $x$ és $y$, amelyekre igaz, hogy $0<x<y<1$. Melyik intervallumban van $x\sqrt[]{y}$? Andi: ,,$\left]0;x\right[$.'' Bulcsú: ,,$\left]x;y\right[$.'' Cecília: ,,$\left]x;1\right[$.'' Dani: ,,$\left]y;1\right[$.'' Emőke: ,,$\left]1;\infty \right[$.'' Ki(k)nek van igaza és miért? (4 pont)   6. $a)$ Győr idén ünnepli várossá válásának 750. évfordulóját. Erre az alkalomra egy építész három kör alakú szökőkutat tervezett úgy, hogy közülük kettő egybevágó, sugaruk hossza 12 méter, kívülről érintik egymást és egy fasort is, amely egy egyenest határoz meg. Milyen hosszú a harmadik szökőkút sugara, ha az kívülről érinti a másik kettőt és a fasor egyenesét is? (A szökőkutak a fasornak ugyanazon az oldalán vannak.) (8 pont) $b)$ Egy másik építész egy hatalmas teret álmodott meg, amelyet tíz, egymást kívülről érintő kör határol. A körök középpontjai egy 121 méter kerületű tízszöget alkotnak. Számítsuk ki a legnagyobb kör $r_1$ sugarát, ha tudjuk, hogy két-két darab $r_2=\frac{1}{3}{r}_1$; $r_3=\frac{1}{3}{r}_2$; $r_4=\frac{1}{3}{r}_3$ és $r_5=\frac{1}{3}{r}_4$ sugarú kör van, a tizedik kör sugara pedig $r_6=\frac{1}{3}{r}_5$. (8 pont)   7. $a)$ Nevesincs-sziget lakói minden számot kétféle kavics sorozatával ábrázolnak. A $▵$ alakú kavics 1-gyel növeli az előtte álló kavicsok által meghatározott számot, a $\otimes$ pedig 7-tel való szorzást jelent. Például a $▵▵▵\otimes ▵\otimes ▵▵$ a 156-os számot jelenti. Legalább hány kavics kell a 2021 kirakásához? (5 pont) $b)$ Janka összegyűjtötte a 2021 kirakásához minimálisan szükséges számú kavicsot, és véletlenszerűen lerakta sorban egymás mellé az összeset. Hány különböző módon történhetett ez meg, ha csak az számít, hogy az adott helyen milyen formájú kavics áll? (5 pont) $c)$ Ezután Janka találomra kivett egy kavicsot a 20-ból, megmutatta barátnőjének, majd visszatette. Ezt még kétszer megismételte. Írjuk fel a $▵$ alakú kavicsok számának eloszlását és határozzuk meg a várható értéket. 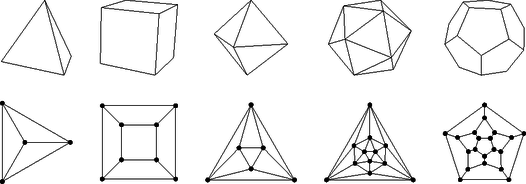(6 pont)   8. $a)$ Az öt szabályos testet a következő síkbeli gráfok segítségével ábrázoltuk. Lehetséges-e bármelyiket a ceruzánk felemelése nélkül megrajzolni úgy, hogy minden élen pontosan egyszer húzzuk át a ceruzát? (6 pont)     $b)$ Marika egységnyi élhosszúságú, pirosra festett kockákból szeretne összeragasztani egy $5\times 5\times 5$-ös nagyobb kockát. Hány gramm ragasztóra van szüksége összesen, ha két kis kocka 1-1 lapját 250 milligramm ragasztóval lehet stabilan összeragasztani? (4 pont) $c)$ Az összeragasztás során kiderült, hogy összesen 150 kiskocka állt Marika rendelkezésére. A kiskockák 8 százaléka cinkből készült, a többi alumíniumból. Marika véletlenszerűen válogatta ki a szükséges kockákat. Legyen az $A$ esemény az, hogy a nagyobb kocka nem lett cinkelt (azaz nem tartalmaz cinket), a $B$ esemény pedig az, hogy a nagyobb kocka az összes cinkből készült kiskockát tartalmazza. Az $A$ vagy a $B$ esemény bekövetkezésének valószínűsége a nagyobb? (6 pont)   9. $a)$ Fricinek 14 nap múlva lesz a szalagavatója, és addigra minél hosszabb szakállat szeretne növeszteni. Most naponta fél millimétert nő a szakálla és éppen ma borotválkozott. A boltban vásárolt egy olyan balzsamot, amelyet közvetlenül borotválkozás után a teljesen sima bőrre kenve, a szakállnövekedés sebessége az előző napi másfélszeresére nő. Legfeljebb milyen hosszú lehet Frici szakálla a szalagavató napján, ha egyik napon sem borotválkozik 1-nél többször? (7 pont) $b)$ Legyen $\alpha$ egy szabályos sokszög külső szögének nagysága és tudjuk, hogy az $(1+\frac{1}{\text{sin}{}^2\alpha })(1+\frac{1}{\text{cos}{}^2\alpha })$ kifejezés értéke a lehető legkisebb. Határozzuk meg a szabályos sokszög csúcsainak számát. (9 pont)