Cím: Kacifántos kerítés - II. rész
Szerző(k):  Schmieder László 
Füzet: 2020/december, 541 - 546. oldal  PDF  |  MathML 
Témakör(ök): Számítástechnika, informatika, Szakmai cikkek, Programozás, algoritmusok

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az első részben az idei Közép-Európai Informatikai Diákolimpia (CEOI) Kacifántos kerítés című feladatát oldottuk meg egy egyszerű, de nem elég hatékony algoritmussal. A megoldás a kerítésen keresett téglalapokat úgy, hogy végighaladt a kerítéselemeken és minden lehetséges bal felső csúcs magasságához megkereste a legtávolabbi jobb alsó csúcsot, majd egy kombinatorikai képlettel megadta az ebben a részben lévő téglalapokat.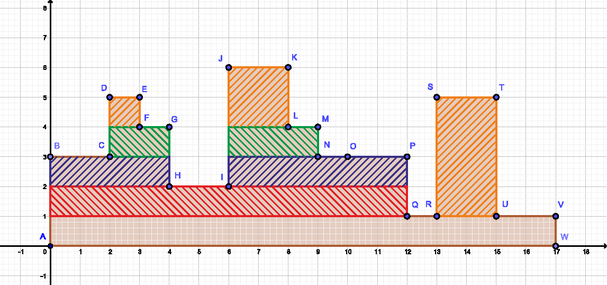
A megoldás hatékonyságának növelése érdekében a kerítés egy más felosztását kellett találnunk, ahol nincs szükség keresésre. Ez a felosztás a kerítés alakjából következik: azok a csúcsok egy kerítéselemen, amelyek y koordinátája nagyobb mindkét szomszédos kerítéselem magasságánál csak olyan téglalapok csúcsai lehetnek, amelyek abban a kerítéselemben vannak. Az ezekből választott bal felső csúcsok jobb alsó párja a kerítéselem jobb alsó csúcsa, tehát azonnal adódik, keresésre nincs szükség.
Nézzük például a hátsó belső borítón megtalálható 1. ábrán a (6,4),L,K,J négyszöget.

 

 

A rajta található téglalapok y>4 koordinátájú bal felső csúcsaihoz csak olyan jobb alsó csúcsok tartozhatnak, amelyek csak ezen a kerítéselemen lehetnek, a legtávolabbi jobb alsó csúcs a (8,0). Ugyanakkor az is látszik, hogy az y≥4 koordinátájú csúcsok csak olyan téglalapok jobb alsó csúcsai lehetnek, amelyek bal felső csúcsa ebben a kerítéselemben van, és a bal felső csúcs y koordinátája 4-nél nagyobb.
Miután megszámoltuk az y>4 bal felső csúcsokhoz tartozó téglalapokat, ezeket a pontokat elhagyhatjuk, mivel jobb alsó csúcsként is már megszámoltuk őket. Tehát a számolás után a kerítés egyszerűsíthető: a szomszédai közül kiemelkedő kerítéselem mindkét szomszédjánál magasabban fekvő csúcsai elhagyhatók. Így egy olyan kerítéselemünk marad, amely valamelyik szomszédjával azonos magasságú. Az előbbi példában a J és K csúcsokkal határolt kerítéselem felső vonalát a továbbiakban a (6,4) és L csúcsok alkotják.
Az előző lépés tovább folytatható: a (6,3),N,M,(6,4) téglalap (amely már két kerítéselem része) y>3 csúcsaival képzett téglalapok megszámolása után az y>3 csúcsok elhagyhatók. Folytatásként az I,(12,2),P,(6,3) téglalap, majd a (0,1),Q,(12,2),(0,2) téglalap következik. Ez az utolsó lépés természetesen csak akkor következhet, ha a (0,2) és HGFEDBC csúcsok által határolt részben lévő téglalapokat már megszámoltuk. Ezek az elhagyások addig folytathatók, amíg végül egy téglalap marad a kerítésből. Az ezen található téglalapok megszámolása az előzőekhez hasonlóan történhet.
A bemutatott eljárás minden lépésében egy ,,kiemelkedő'' téglalapot kapunk, amelynek alsó és jobb oldala kivételével minden pontja olyan téglalapok bal felső csúcsa, melyekhez csak az adott kiemelkedésben és alatta találhatóak a számolásnál figyelembe veendő jobb alsó csúcsok. Az előbbi példában bemutatott (6,4),L,K,J téglalap esetében a (b,f) bal felső csúcsok koordinátáira igaz, hogy 6≤b<8 és 4<f≤6, és a hozzájuk tartozó (j,a) jobb alsó csúcsok koordinátáira teljesül, hogy b<j≤8 és 0≤a<f.
Nézzük általánosan, tehát legyen egy, az eljárásban talált téglalap bal felső csúcsa (bal,fent) és jobb alsó csúcsa (jobb,lent). Az elhagyása előtt megszámolandó téglalapok (b,f) bal felső csúcsának koordinátáira teljesül, hogy bal≤b<jobb és lent<f≤fent, míg (j,a) jobb alsó csúcsainak koordinátáira igaz, hogy b<j≤jobb és 0≤a<f. Egy adott (b,f) bal felső csúcshoz tartozó téglalapok száma tehát (jobb-b)⋅(f-0). Ezeket összegezve a lehetséges (b,f) csúcsokra a téglalapok száma:
∑b=baljobb-1∑f=lent+1fent(jobb-b)⋅(f-0).

Ebben az összegben minden előforduló (jobb-b) tényezőt megszorzunk minden f értékkel. A szorzás és az összeadás asszociativitása következében ezt úgy is végezhetjük, hogy először összegezzük a tényezőket külön-külön, majd az így kapott mennyiségeket szorozzuk össze. Tehát a kifejezés kevesebb szorzással fölírva:
∑b=baljobb-1(jobb-b)⋅∑f=lent+1fentf.
Ebben két számtani sorozat szorzata szerepel, tehát az összegképlet alapján az eredmény:
(jobb-bal+1)⋅(jobb-bal)2⋅(lent+1+fent)⋅(fent-lent)2.
A téglalapok megszámolását tehát megkapjuk a fenti eredmény alapján. Most már csak az a kérdés, hogy miként találjuk meg az ,,elhagyható'' kerítésrészeket, amelyek a szomszédos kerítésrészeknél magasabbak. Az algoritmus nem végezhet a kerítéselemeken átnyúló keresést, tehát például a kerítéselemek eredeti sorrendjében kellene haladnia.
 

1. feladat: Vizsgáljuk meg az 1. ábrát, és vegyük észre, hogy milyen jellemző tulajdonságok alapján találjuk meg a keresett kiemelkedéseket!
 

Haladjunk a kerítés felső vonalán. Az első kiemelkedés a (2,3),F,E,D, amelyet az F csúcs zár. Ezt a részt elhagyva és a kerítés vonalán lefelé haladva a (4,3) pontban érünk a C csúcs magasságába, így a C,(4,3),G,(2,4) téglalapot találjuk. Ennek levágása után a kerítés vonalán tovább menve a H csúcsban érünk egy kiemelkedés legjobboldalibb és legalsó pontjához, így elhagyhatjuk a (0,2),H,(4,v3),B téglalapot.
Megfigyelhető, hogy a kerítés vonalán egy csúcstól az alatta lévő csúcsig haladva találunk olyan pontot, amely egy kiemelkedés jobb alsó sarka. A megtaláláshoz csak azt kell tudnunk, hogy a vizsgált kerítésrész jobb oldalához melyik bal oldal tartozik. Nézzük a borítón lévő 2. ábrát.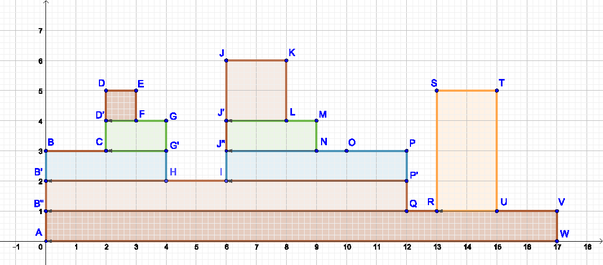
 

 

Az első lefelé haladás az EF szakaszon történik, ahol az F csúcs egy jobb alsó sarok, melynek bal alsó párja a kiemelkedés bal oldalán, a CD szakaszon található. Számoljuk meg a talált kerítésrészhez tartozó téglalapokat, majd hagyjuk el a D és E csúcsokat, és vegyünk föl egy új csúcsot, D'-t. A kerítés vonalán a következő lefelé haladás a GH szakaszon történik, a bal oldal pedig továbbra is a CD' szakaszra esik, így a G'C szakasz feletti rész téglalapjai megszámolandók és a D', F, G csúcsok elhagyhatók. Az ábrán a kiemelkedések jobb alsó csúcsától a bal alsó csúcsáig egy-egy nyíl mutat.
Továbbhaladva a kerítés vonalán lefelé a H pontba jutunk, azonban a hozzá tartozó bal oldal már nem a CD egyenesre esik, hanem az attól balra eső AB szakaszra. Ez éppen az a rész, ahol a CD szakaszt megelőzően fölfelé haladtunk. Így látható, hogy a kerítés vonalán a fölfelé és lefelé haladó mozgások szakaszai párba állíthatók. Ha továbbhaladunk a kerítés vonalán, akkor megfigyelhetjük ezeket a párokat az IJKLMNOPQ részen haladva is. Itt az utolsó szakaszon lefelé mozogva a Q ponthoz tartozó bal alsó csúcs ismét az AB szakaszra esik, miután az P'I fölötti kerítésrészt is elhagytuk.
 

2. feladat: Adjuk meg, hogyan lehetne könnyen megtalálni egy-egy ,,kiemelkedés'' jobb alsó csúcsához a bal alsó csúcsot, tehát a 2. ábrán jelölt nyilak végpontját!
 

Induljunk el a kerítés bal alsó csúcsától fölfelé és haladjunk végig a kerítés vonalán annak jobb oldali legalsó csúcsáig. Minden fölfelé haladásnak megvan a lefelé haladás párja a kerítés vonalán való mozgás során. Ezek a párok alkotják a kiemelkedések bal és jobb oldali szakaszát. A párok úgy következnek a kerítés vonalán, mint egy kifejezés nyitó és csukó zárójelei, vagyis egymásba ágyazva. Ha egy felfelé mozgás megelőz egy másikat, akkor a hozzá tartozó lefelé haladás később jön, a másikhoz tartozó lefelé mozgás után. Ez egy helyesen zárójelezett kifejezésnél is pontosan így van. Amikor egy kifejezést kiértékelünk, akkor a legbelső zárójelben lévő részt számoljuk ki, majd a zárójeleket elhagyva folytatjuk a számolást. Itt pontosan ugyanezt kell tennünk, csak a kifejezés helyett a téglalapok megszámolását végezzük el, majd a kiemelkedő részt elhagyjuk, ahogyan a kifejezésnél a zárójeleket.
Az egymásba ágyazás, a belső párok elhagyása azt sugallja, hogy használjunk vermet a bal oldali szakaszok tárolására. A verem tetején mindig az a szakasz lesz, amelynek jobb oldali párja elsőként következik. A kerítés vonalán való haladás során minden felfelé mozgás egy új pár bal oldalát helyezi a veremre, míg a lefelé haladás egy párt vesz majd ki a veremből. Illetve ez csak akkor teljesül, ha a felfelé és lefelé haladás ugyanolyan magasról indult, tehát például a 2. ábrán az RSTU kiemelkedésnél. Általában kicsit összetettebb a helyzet. Például az I csúcstól fölfelé mozogva először tegyük a verem tetejére az IJ szakaszt, majd a KL szakaszon lefelé haladva a verem tetején lévő szakaszt cseréljük az IJ' szakaszra. Továbbhaladva a kerítésen az MN szakaszon lefelé változtassuk a verem tetején lévő szakaszt I''J-re. Innen továbblépve a PP' szakaszon lefelé haladva vesszük ki az IJ'' szakaszt a veremből. Figyelnünk kell tehát, hogy a lefelé mozgások során a verem tetején lévő szakasz alsó csúcsa és a lefelé mozgás szakaszának alsó csúcsa hogyan viszonyul egymáshoz. Innen látszik, hogy elegendő a veremben a felfelé haladó szakaszok alsó csúcsát elhelyezni, a felső csúcsra nincs szükség.
A program elkészítéséhez először be kell olvasnunk az adatokat, majd azokból meg kell adnunk a kerítés vonalán haladáskor érintett csúcsokat. Az 1. ábrán ezeket a csúcsokat betűkkel jelöltük, melyeken ABC rendben fogunk végighaladni. Ezek a csúcsok a bemenetként kapott kerítéselemek magasságából és szélességéből számíthatók, a bemenet sorrendjében követik egymást. Így a bemenet feldolgozásakor egy lineáris futásidejű algoritmussal megadhatjuk a csúcsokat. Ennek a programrésznek az elkészítését az olvasóra bízzuk. Feltételezzük a továbbiakban, hogy a következő programrészek futása előtt már rendelkezésünkre áll egy 2N+2 méretű pont[0..2N+1] tömb, amely sorrendben tartalmazza a kerítés vonalán érintett csúcsok (x,y) koordinátáit.
Ezen előkészítés után következzen a kerítés vonalának bejárása. Vegyünk föl egy v vermet, amely a pont[ ] tömb csúcsainak sorszámát tárolja, azaz a futás során legföljebb 2N+1 csúcs indexét. Helyezzünk a verem tetejére egy 0-t, az első csúcs sorszámát. Amikor ez a csúcs kikerül a verem tetejéről, akkor bejártuk a kerítés teljes vonalát, tehát az üres verem jelzi a műveletsor végét. A bal és jobb változók mutatják, hogy a bejárás melyik csúcsokat vizsgálja. Kezdetben az első kerítéselem két felső pontjának sorszámát tartalmazzák.
 


1. Függvény KacifantosKerites2(N,h[0..N-1],w[0..N-1]) : Egész
2. BeolvasasCsucsepites(N,h,w,pont)
3. darab := 0
4. v.Verembe(0)
5. bal := 1
6. jobb := 2
7. Ciklus amíg nem v.Üres( )

 

A végeredményt adó függvényt több részletben írjuk le, tehát az algoritmusrészletek és magyarázatok felváltva követik egymást. A jobb érthetőség érdekében a függvény sorait számozzuk. A ciklusmagban egy elágazás szerepel, amelyben először megállapítjuk, hogy a kerítésen történő mozgás a jobb és az utána következő csúcs között milyen irányú. Ha felfelé haladunk a kerítés vonalán, akkor vermeljük a jobb oldali alsó csúcsot, vagyis megjegyezzük, hogy itt van egy kerítésrész bal oldali alsó csúcsa, majd továbblépünk a következő kerítéselemre. Ha azonos magasságú kerítéselemek vannak egymás mellett, akkor egyszerűen átmegyünk a következőre.
 


8.  Ha pont[jobb].y < pont[jobb+1].y akkor
9.  v.Verembe(jobb)
10.  bal := jobb+1
11.  jobb := jobb+2
12.  egyébként ha pont[jobb].y = pont[jobb+1].y akkor
13.  jobb := jobb+2
14.  egyébként

 

Az elágazás utolsó része a leginkább összetett, vagyis amikor lefelé haladunk a kerítés vonalán, tehát amikor pont[jobb]>pont[jobb+1]. Ekkor három esetet különböztetünk meg aszerint, hogy a verem tetején lévő csúcs milyen magasan van a jobb után következő csúcshoz képest.
 


15.  Ha pont[v.Felső( )].y > pont[jobb+1].y akkor
16.  szamol(darab,pont[v.Felső( )].x, pont[jobb].y, pont[jobb].x, pont[v.Felső( )].y)
17.  pont[jobb].y := pont[v.Felső( )].y
18.  v.Veremből( )
19.  bal := v.Felső( )+1

 

Amikor a verem tetejéhez tartozó csúcs van magasabban, akkor csak az ő magasságáig lévő téglalapot mint kiemelkedést számoljuk meg és hagyjuk el. A példában ilyen eset a GH szakaszon történő lefelé mozgás. Ekkor a veremben az A és a C csúcs indexe van, a tetején a C csúcs sorszáma. Mivel a C csúcs magasabban van, mint a G csúcs, ezért a jobb indexnél lévő G csúcsot módosítjuk G'-re (ezzel hagytuk el a kiemelkedést), majd kivesszük a veremből a C csúcs sorszámát, ahol most egyedül az A csúcs indexe van. Ezután megadjuk a bal változóban a bal oldali felfelé menő rész felső csúcsának indexét, a példában a B csúcsot. Így a folytatásként szóba jöhető kiemelkedés a bal oldala az AB szakasz, jobb oldala a G'H szakasz.
 


20.  egyébként ha pont[v.Felső( )].y = pont[jobb+1].y akkor
21.  szamol(darab, pont[v.Felső( )].x, pont[jobb].y, pont[jobb].x, pont[v.Felső( )].y)
22.  v.Veremből( )
23.  Ha nem v.Üres( ) akkor
24.  bal := v.Felső( )+1
25.  jobb := jobb+2
26.  Elágazás vége

 

Amikor a verem legfelső eleme által hivatkozott csúcs azonos magasságban van a lefelé mozgás alsó csúcsával, akkor a kiemelkedés megszámolása után elhagyjuk ezt a kerítésrészt, vagyis kivesszük a veremből a tetején lévő elemet és továbblépünk előre a jobb változóval. Természetesen ezt csak akkor tehetjük meg, ha nem a 0-ás csúcsot vettük ki a veremből, hiszen azzal már befejeztük a bejárást. Az ábrán például az RSTU kiemelkedésnél az R csúcsra mutat a verem felső száma és a TU szakaszon mozgunk lefelé. Ekkor a számolás után a verem tetején az A csúcs sorszáma található, a bal változó a B'' csúcsra, míg a jobb a V csúcsra hivatkozik.
 


27.  egyébként
28.  szamol(darab, pont[v.Felső( )].x, pont[jobb].y, pont[jobb].x, pont[jobb+1].y)
29.  pont[bal].y := pont[jobb+1].y
30.  jobb := jobb + 2
31.  Elágazás vége
32.  Elágazás vége
33. Ciklus vége
34. KacinfatosKerates2 := darab
35. Függvény KacifantosKerites2 vége

 

A harmadik eset az a lehetőség, amikor a verem teteje által mutatott csúcs magassága kisebb, mint a lefelé mozgás alsó csúcsának magassága. Ekkor szintén megszámoljuk a kiemelkedő téglalaprészben lévő téglalapokat, majd a bal oldali szakasz felső csúcsának magasságát állítjuk a jobb oldali szakasz alsó csúcsának magasságára. Ez történik a példában, amikor az MN szakaszon mozgunk lefelé, és a J' csúcsból a J'' csúcsba lépünk.
A megoldást adó függvény a ciklus befejezése után nem tesz mást, mint a megszámolt téglalapok darab változóban lévő értékét visszaadja. Ehhez az algoritmusban többször is szereplő szamol(darab,bal,fent,jobb,lent) függvényt hívja meg minden kiemelkedő rész elhagyása előtt. A függvényben csak szorzás és 2-vel való osztás szerepel a korábban kiszámított képlet alapján. Csupán arra kell ügyelnünk, hogy a kifejezésben lévő mennyiségek szorzata igen nagy lehet, ezért túlcsordulás történhet. Ennek elkerülésére a mennyiségek 1 000 000 007-tel vett maradékait kell szoroznunk, illetve a szorzat maradékát hozzáadnunk a darab eddigi értékéhez. Ennek a függvénynek a megírását is az olvasóra bízzuk azzal a megjegyzéssel, hogy a 2-vel való maradékos osztásnál figyeljünk arra, hogy a szorzatok tényezői közül csak a párosakat osszuk.
Ezen algoritmus lépésszáma a bemenet N elemszámával arányos, tehát a program lineáris futásidejű, így a versenyen is megállta volna a helyét hatékonyság szempontjából is.
 Schmieder László