Cím:	Megoldások a 2020/8. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Bíró Bálint, Eger
Füzet:	2020/december, 519 - 536. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Mely $x$ valós számokra értelmezhető az $\begin{array}{c}{\displaystyle f\left(x\right)=\sqrt[]{\frac{1-\sqrt[]{x-3}}{\text{log}{}_2\left(x-2\right)}}}\end{array}$ függvény? (5 pont) $b)$ Adjunk meg legalább két olyan valós számot, amelyekkel a $\begin{array}{c}{\displaystyle \sqrt[]{x-2}+\sqrt[]{2x+3}=\sqrt[]{3x+7}}\end{array}$ és a $\begin{array}{c}{\displaystyle {16}^x\cdot 8^{2x}\cdot 4^{6x}\cdot \sqrt[]{2}=64}\end{array}$ egyenletek valós gyökei valamilyen sorrendben egy-egy számtani sorozat egymás utáni tagjai lehetnek. (6 pont)   Megoldás. $a)$ A logaritmus értelmezése miatt $x-2>0$, azaz $x>2$. Ugyanakkor $\text{log}{}_2\left(x-2\right)\ne 0$, tehát $x-2\ne 1$, vagyis $x\ne 3$. A négyzetgyök értelmezéséből $x-3\ge 0$, illetve $x\ge 3$ következik. Ez az előző eredménnyel együtt azt jelenti, hogy $\begin{array}{c}{\displaystyle x>3.}\end{array}$ (1) Ugyancsak a négyzetgyök értelmezése szerint $\begin{array}{c}{\displaystyle \frac{1-\sqrt[]{x-3}}{\text{log}{}_2\left(x-2\right)}\ge 0.}\end{array}$ (2) Ez kétféleképpen lehetséges: $•$ vagy $1-\sqrt[]{x-3}\ge 0$ és $\text{log}{}_2\left(x-2\right)>0$, $•$ vagy pedig $1-\sqrt[]{x-3}\le 0$ és $\text{log}{}_2\left(x-2\right)<0$. Az első esetből egyrészt azt kapjuk, hogy $1\ge \sqrt[]{x-3}$, innen pedig azt, hogy $x\le 4$. Másrészt $\text{log}{}_2\left(x-2\right)>0$, vagy másként $\text{log}{}_2\left(x-2\right)>\text{log}{}_{2}1$ és a $g\left(x\right)=\text{log}{}_2\left(x-2\right)$ függvény szigorúan monoton növekedése miatt $x-2>1$, tehát $x>3$. Eredményeinket összevetve azt kapjuk, hogy a (2) egyenlőtlenség a $\left]3;4\right]$ halmazon teljesül. Ha pedig $1-\sqrt[]{x-3}\le 0$, akkor ebből $x\ge 4$ adódik, a $\text{log}{}_2\left(x-2\right)<0$ egyenlőtlenségnek eleget tevő valós számokra $x<3$ áll fenn. Ez azonban ellentmond az (1) feltételnek. Az $f\left(x\right)$ függvény értelmezési tartománya ezért a $D_f=\left]3;4\right]$ számhalmaz. $b)$ A négyzetgyökös egyenletben szereplő első négyzetgyök értelmezése miatt $x-2\ge 0$, azaz $x\ge 2$, ezekre a valós számokra a másik két gyökös kifejezés is értelmezett, hiszen $x\ge 2$ esetén $2x+3>0$ és $3x+7>0$ érvényes. Az egyenlet mindkét oldalát négyzetre emelve rendezés után a $\begin{array}{c}{\displaystyle \sqrt[]{\left(x-2\right)\cdot \left(2x+3\right)}=3}\end{array}$ egyenletet kapjuk. Ennek mindkét oldalát ismét négyzetre emelhetjük, ahonnan rendezéssel a $2x^2-x-15=0$ másodfokú egyenletet kapjuk, amelynek gyökei: $x_1=3$, $x_2=-2\mathrm{,}5$. Az $x_2=-2\mathrm{,}5$ ellentmond az $x\ge 2$ feltételnek, ezért nem megoldás. Az $x_1=3$ megoldása a négyzetgyökös egyenletnek, ezt egyszerű számolással ellenőrizhetjük. Tekintsük ezután az exponenciális egyenletet. Ez átírható: $\begin{array}{c}{\displaystyle 2^{4x}\cdot 2^{6x}\cdot 2^{12x}\cdot 2^{\frac{1}{2}}=2^{22x+\frac{1}{2}}=2^6\mathrm{,}}\end{array}$ ahonnan az exponenciális függvény kölcsönösen egyértelmű tulajdonsága miatt $\begin{array}{c}{\displaystyle 22x+\frac{1}{2}=6.}\end{array}$ Ennek gyöke az $x=\frac{1}{4}$ valós szám, ez az exponenciális egyenlet megoldása. Olyan valós számokat kell megadnunk, amelyekkel együtt az egyenletek megoldásai egy-egy számtani sorozat szomszédos tagjai lesznek. Például a megoldások számtani közepét véve: $\begin{array}{c}{\displaystyle a=\frac{3+\frac{1}{4}}{2}=\frac{13}{8}\mathrm{,}}\end{array}$ ekkor az $\frac{1}{4}$, $\frac{13}{8}$, 3 számok egy számtani sorozat szomszédos tagjai. Lehetséges az is, hogy $\begin{array}{c}{\displaystyle \frac{\frac{1}{4}+b}{2}=\mathrm{3,}}\end{array}$ ahonnan $b=\frac{23}{4}$, így az $\frac{1}{4}$, 3, $\frac{23}{4}$ számok egy másik számtani sorozat szomszédos tagjai.   Megjegyzés. Számtani sorozatot alkotnak a $-\frac{5}{2}$, $\frac{1}{4}$, 3 számok is, ahol a sorozat első tagját a $\begin{array}{c}{\displaystyle \frac{c+3}{2}=\frac{1}{4}}\end{array}$ egyenletből kaptuk.     2. Az Agatha Christie műveiből készült Poirot-novellák című tv-sorozat ,,A csokoládésdoboz'' című epizódjának egyik jelenetében két szereplő, egy férfi és egy nő, egy operaelőadás hallgatása közben egy doboz belga csokoládét kóstolgatott. A dobozt a jelenet kezdetén bontották fel, és a dobozban kezdetben $7$-féle csokoládéfigura volt, mindegyikből $4$ darab az ábra szerint.     A női szereplő kedvence a korona alakú csokoládé. Kóstolgatás közben az udvariasság szabályai szerint mindig a hölgy választ először, aztán a férfi, majd újra a hölgy, aztán a férfi és így tovább. A férfi tudja, hogy a hölgy kedvence a koronás csokoládé, ezért ő sosem választ magának ilyet. Ezek figyelembevételével először elfogyasztanak $7$ csokoládét, mindegyik fajtából egyet-egyet, mégpedig úgy, hogy a hölgy először a kedvencéből választ. $a)$ Hányféle sorrendben fogyaszthatnák el a $7$ csokoládét? (6 pont) $b)$ Ha a megmaradt $21$ csokoládéból a hölgy egyesével, véletlenszerűen és visszatevés nélkül kiválasztana 6 darabot, akkor mennyi lenne a valószínűsége, hogy azok között legalább $2$ koronás csokoládét talál? (6 pont)   Megoldás. $a)$ A nő először a koronás csokoládéból választ, ezt $4$-féleképpen teheti meg, hiszen mindegyik csokoládéból 4-4 darab van. Ebből már nem választ egyikük sem az első 7 csokoládé kóstolása során. Ezután a férfi a megmaradt $6$-féle csokoládéból választ egy fajtát és kivesz belőle egyet, ezt $6\cdot 4=24$ különböző módon teheti meg. Ezt követően ismét a hölgy választ egy csokoládét, mégpedig $5$-féléből, de bármelyiket is választja a $5$ fajta közül, mindegyikből $4$ választási lehetősége van, ezért $5\cdot 4=20$-féleképpen választhat. Ennek alapján könnyen látható, hogy a férfi további választási lehetőségeinek száma $4\cdot 4=16$, $4\cdot 2=8$, a nő további csokoládé-kiválasztási lehetőségeinek száma pedig $3\cdot 4=12$, $1\cdot 4=4$. A jelenetben szereplő nő és férfi tehát az első $7$ csokoládét $4\cdot 24\cdot 20\cdot 16\cdot 12\cdot 8\cdot 4=11796480$ különböző sorrendben fogyaszthatná el. $b)$ Egyszerűbb először a komplementer esemény valószínűségét kiszámolni, vagyis azt, hogy a kiválasztottak közül egy sem lesz, illetve egy darab lesz koronás csokoládé. Legyen ezek valószínűsége $p_0$, illetve $p_1$. Mivel egyesével és visszatevés nélkül választ a hölgy, ezért alkalmazhatjuk a hipergeometrikus eloszlási formulát. Tudjuk, hogy $3$ darab koronás csokoládé maradt meg, ezért $p_0$ kiszámításához a kedvező esetek száma $\left(\genfrac{}{}{0ex}{}{3}{0}\right)\cdot \left(\genfrac{}{}{0ex}{}{18}{6}\right)=18564$, az összes eset száma pedig $\left(\genfrac{}{}{0ex}{}{21}{6}\right)=54264$, és így $\begin{array}{c}{\displaystyle p_0=\frac{18564}{54264}=0\mathrm{,}3421.}\end{array}$ Ha $p_1$-et szeretnénk kiszámítani, akkor a kedvező esetek száma $\left(\genfrac{}{}{0ex}{}{3}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{18}{5}\right)=25704$, az összes eset száma ugyanannyi, mint az előbb, ezért $\begin{array}{c}{\displaystyle p_1=\frac{25704}{54264}=0\mathrm{,}4737.}\end{array}$ Annak az $A$ eseménynek a valószínűsége tehát, hogy a jelenet női szereplője a kiválasztási feltételek figyelembevételével a $6$ csokoládé között legalább $2$ koronásat talál: $p\left(A\right)=1-\left(p_0+p_1\right)=0\mathrm{,}1842$.   3. Anna és Boglárka unokatestvérek, az egyik megyeszékhely különböző iskoláiba járnak. Anna kilenc évvel idősebb Boglárkánál. Jelöljük Anna jelenlegi életkorát $A$-val, Boglárka jelenlegi életkorát $B$-vel $(A$ és $B$ pozitív egész számok$)\mathrm{.}$ $a)$ Lehetséges-e, hogy $n$ $(n$ pozitív egész$)$ év múlva Anna éppen háromszor olyan idős lesz, mint Boglárka? Hány év múlva fordulhat elő, hogy Anna kétszer olyan idős lesz, mint Boglárka? $($Válaszunkat indokoljuk.$)$ (4 pont) Anna és Boglárka is nagyon ügyesek matematikából. Órai teljesítményük, eddigi versenyeredményeik alapján a tanáraik benevezték őket egy matematikaversenyre. Anna matematika szakkörön is készül a versenyre. A szakkörre $21$ tanuló jár, $9$ lány és $12$ fiú. A csoport diákjai mindannyian jó képességűek. A tanáruk úgy szeretné összeállítani a versenyre utazó $14$ fős csapatot, hogy azon belül a nemek aránya azonos legyen a szakkörön belüli arányukkal. $b)$ Hányféleképpen állíthatja össze a versenyre utazó csapatot Anna szakkörének tanára? (3 pont) Anna a matematika területein belül legjobban a geometriát szereti. Egyszer rajzolt Boglárkának egy derékszögű trapézt és elmagyarázta unokatestvérének a trapéz tulajdonságait. Anna rajza az $ABCD$ trapéz, amelyben a $DA$ szár merőleges az $AB$ alapra. $c)$ Lehetséges-e, hogy a $CD$, $DA$, $AB$, $BC$ szakaszok hossza ebben a sorrendben egy mértani sorozat négy szomszédos tagja? (Válaszunkat indokoljuk.) (7 pont)   Megoldás. $a)$ Az első kérdésre az $A+n=3\cdot \left(B+n\right)$ egyenlet tanulmányozása után válaszolhatunk. Az egyenlet rendezése után azt kapjuk, hogy $A-B=2B+2n$. Tudjuk, hogy $A-B=9$, tehát ha lehetséges volna, hogy $n$ év múlva Anna éppen háromszor olyan idős legyen, mint Boglárka, akkor teljesülnie kellene a $9=2B+2n$ egyenletnek. Ez azonban nem lehetséges, mert az egyenlet bal oldala páratlan, míg a jobb oldal páros pozitív egész szám. A második kérdés megválaszolásához az $A+m=2\cdot \left(B+m\right)$ egyenlet megoldhatóságát vizsgáljuk, ahol $m$ pozitív egész szám. Ismét felhasználva az $A-B=9$ feltételt, a $9=B+m$ egyenletet kapjuk. A feladat szövege szerint Boglárka már iskolába jár, ezért $B\ge 6$. Ugyanakkor $B<9$, hiszen $B\ge 9$ esetén nem teljesülne a $9=B+m$ egyenlet egyetlen pozitív egész $m$-re sem. Eszerint csak $m=3$, $m=2$, $m=1$ lehetséges, ekkor Boglárka rendre 6, 7, 8 éves, Anna pedig rendre 15, 16, 17 éves. Az $m$ szám mindhárom értékét figyelembe véve, $m$ év múlva Anna $18$, Boglárka pedig $9$ éves lesz. $b)$ Anna matematika szakkörében a lányok és a fiúk számának aránya $\frac{9}{12}=\frac{3}{4}$. Ez azt jelenti, hogy a versenyre kijelölt $14$ fős csoportban $6$ lány és $8$ fiú lesz, hiszen akkor a versenyre kijelöltek között a lányok és fiúk számának aránya $\frac{6}{8}=\frac{3}{4}$. A feladat szövegéből tudjuk, hogy Annát a szakkör tanára benevezte a versenyre, tehát a többi lány közül még 5-öt kell kiválasztania, ezt $\left(\genfrac{}{}{0ex}{}{8}{5}\right)=56$-féle módon teheti. A versenyre utazó fiúk kiválasztása $\left(\genfrac{}{}{0ex}{}{12}{8}\right)=495$ különböző módon valósulhat meg. Anna szakköréből a versenyre utazó csapat kiválasztása ezért $56\cdot 495=27720$-féle módon lehetséges. $c)$ A feladat nyilvánvaló megoldása az, amikor a mértani sorozat hányadosa $1$, ekkor egyszerűen belátható, hogy a trapéz minden oldala egyenlő hosszú, és mivel derékszögű is, ezért négyzet. Tegyük fel a továbbiakban, hogy a mértani sorozat hányadosa nem $1$, és tekintsük az ennek megfelelő 3.1. ábrát, ahol a $CD$, $DA$, $AB$, $BC$ szakaszok hosszát rendre $a$, $a\cdot q$, $a\cdot q^2$, $a\cdot q^3$-nel jelöltük, ahol $q$ a mértani sorozat hányadosa. 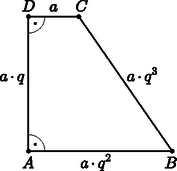    3. 1. ábra 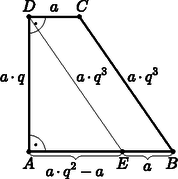    3. 2. ábra   Húzzunk párhuzamost a $BC$ szárral a $D$ ponton keresztül, ekkor az $EDA$ derékszögű háromszöget és a $BCDE$ parallelogrammát kapjuk. A parallelogramma tulajdonsága miatt $DE=a\cdot q^3$, $BE=a$, így $AE=a\cdot q^2-a$ (3.2. ábra). Az $EDA$ derékszögű háromszögre felírhatjuk a Pitagorasz-tételt: $\begin{array}{c}{\displaystyle {\left(a\cdot q\right)}^2+{\left(a\cdot q^2-a\right)}^2={\left(a\cdot q^3\right)}^2\mathrm{.}}\end{array}$ A műveletek elvégzése és az $a^2>0$ számmal való osztás után $q^2+q^4-2q^2+1=q^6$, ahonnan a $q^2=x$ helyettesítéssel és rendezéssel az $x^3-x^2+x-1=0$ egyenletet kapjuk. Ebből szorzattá alakítással adódik, hogy $\left(x-1\right)\cdot \left(x^2+1\right)=0$. Nyilvánvaló, hogy a valós számok halmazán $x^2+1\ne 0$, ezért csak $x-1=0$ lehetséges. Ekkor $x=1$, azaz $q^2=1$, és mivel $q>0$, ezért $q=1$. Jelen számításainkban azonban föltettük, hogy $q\ne 1$, ezért ez nem ad újabb megoldást. A feladat egyetlen megoldása tehát az, amikor a mértani sorozat hányadosa $1$, azaz, amikor a derékszögű trapéz négyzet. Ha Anna rajza minden feltételnek megfelelt, akkor négyzetet rajzolt Boglárkának.   Megjegyzés. A számítások akkor is ugyanerre az eredményre vezetnek, ha a rajzok $0<q<1$ hányadost feltételezve készülnek.   4. A koronavírus $2020.$ évi elterjedésével kapcsolatos adatokat a grafikonon szemlélhetjük $($forrás: pandemia.hu).     A grafikon egyes adatait táblázatba foglaltuk márciustól szeptemberig minden hónap $6$-án.   ${\displaystyle \begin{array}{|cc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">Fertőzöttek száma</span>}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">03.06.</span>}}\hfill & \hfill {\displaystyle \text{4}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">04.06.</span>}}\hfill & \hfill {\displaystyle \text{744}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">05.06.</span>}}\hfill & \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">06.06.</span>}}\hfill & \hfill {\displaystyle \text{3990}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">07.06.</span>}}\hfill & \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">08.06.</span>}}\hfill & \hfill {\displaystyle \text{4597}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">09.06.</span>}}\hfill & \hfill {\displaystyle \text{8387}}\hfill \\ \hline\end{array}}$   A következő táblázatban két tizedesjegyre kerekítve feltüntettük a magyarországi fertőzöttek számának napi átlagos növekedését az egyes időpontok között eltelt idő alatt (a megjelölt időpontok között eltelt napok számát megállapodás szerint úgy számítjuk, hogy az időintervallum felső időpontjának napját hozzászámítjuk az intervallumhoz, az alsó értéket nem).   ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{03.06.‐04.06.}}\hfill & \hfill {\displaystyle \text{04.06.‐05.06.}}\hfill & \hfill {\displaystyle \text{05.06.‐06.06.}}\hfill & \hfill {\displaystyle \text{06.06.‐07.06.}}\hfill & \hfill {\displaystyle \text{07.06.‐08.06.}}\hfill & \hfill {\displaystyle \text{08.06.‐09.06.}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{78,9}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{6,63}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill \\ \hline\end{array}}$   $a)$ Töltsük ki mindkét táblázat hiányzó részeit (egy-egy napon a fertőzöttek száma csak pozitív egész szám lehet, ezért a számítások során a kerekítés szabályainak megfelelően járjunk el). (4 pont) $b)$ Egy $n$ pontú teljes gráf élei közül $21$ élet törölve egy fagráfot kapunk. Határozzuk meg $n$ értékét. (5 pont) $c)$ Bizonyítsuk be, hogy a ${11}^n+{60}^n\le {61}^n$ egyenlőtlenség $n=1$ kivételével minden pozitív egész számra teljesül. (5 pont)   Megoldás. $a)$ Az első táblázat szerint március 6. és április 6. között 740-nel nőtt a fertőzöttek száma, és mivel a két időpont között $31$ nap telt el (március 31 napos), ezért ez alatt az idő alatt naponta átlagosan $\frac{740}{31}=23\mathrm{,}87$ fővel növekedett a fertőzöttek száma. Április 6. és május 6. között a megállapodás szerint számolva 30 nap telt el (április 30 napos), így a május 6-án az első táblázatban szereplő értéket $x$-szel jelölve és felhasználva, hogy a második táblázat szerint ebben az időszakban átlagosan naponta 78,9-del nőtt a fertőzöttek száma: $\begin{array}{c}{\displaystyle \frac{x-744}{30}=78\mathrm{,}\mathrm{9,}}\end{array}$ ahonnan egészre kerekítve $x=3111$, ennyi volt a fertőzöttek száma május 6-án. A kapott eredmény segítségével kitölthetjük a második táblázat harmadik oszlopának hiányzó adatát, figyelembe véve, hogy május 6. és június 6. között 31 nap telt el. Ekkor a fertőzöttek számának átlagos napi növekedése $\begin{array}{c}{\displaystyle \frac{3990-3111}{31}=28\mathrm{,}35.}\end{array}$ Az első táblázatnak a július 6-ára vonatkozó hiányzó adatát $y$-nal jelölve felírhatjuk, hogy $\begin{array}{c}{\displaystyle \frac{y-3990}{30}=6\mathrm{,}\mathrm{63,}}\end{array}$ hiszen a két időpont között most 30 nap telt el. Ebből adódik, hogy kerekítve $y=4189$. Első táblázatunk most már teljes, kitölthetjük a második táblázat két hiányzó értékét. Eszerint július 6. és augusztus 6., illetve augusztus 6. és szeptember 6. között (július és augusztus is 31 napos) $\begin{array}{c}{\displaystyle \frac{4597-4189}{31}=13\mathrm{,}16;\frac{8387-4597}{31}=122\mathrm{,}26}\end{array}$ volt a magyarországi fertőzöttek számának napi átlagos növekedése. Kitöltött táblázataink:   ${\displaystyle \begin{array}{|cc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">Fertőzöttek száma</span>}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">03.06.</span>}}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">04.06.</span>}}\hfill & \hfill {\displaystyle \text{ 744 }}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">05.06.</span>}}\hfill & \hfill {\displaystyle \text{ 3111 }}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">06.06.</span>}}\hfill & \hfill {\displaystyle \text{ 3990 }}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">07.06.</span>}}\hfill & \hfill {\displaystyle \text{ 4189 }}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">08.06.</span>}}\hfill & \hfill {\displaystyle \text{ 4597 }}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">09.06.</span>}}\hfill & \hfill {\displaystyle \text{ 8387 }}\hfill \\ \hline\end{array}}$   ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{03.06.‐04.06.}}\hfill & \hfill {\displaystyle \text{04.06.‐05.06.}}\hfill & \hfill {\displaystyle \text{05.06.‐06.06.}}\hfill & \hfill {\displaystyle \text{06.06.‐07.06.}}\hfill & \hfill {\displaystyle \text{07.06.‐08.06.}}\hfill & \hfill {\displaystyle \text{08.06.‐09.06.}}\hfill \\ \hfill {\displaystyle \text{23,87}}\hfill & \hfill {\displaystyle \text{ 78,9}}\hfill & \hfill {\displaystyle \text{ 28,35}}\hfill & \hfill {\displaystyle \text{ 6,63}}\hfill & \hfill {\displaystyle \text{ 13,16}}\hfill & \hfill {\displaystyle \text{ 122,26 }}\hfill \\ \hline\end{array}}$   $b)$ Az $n$ pontú teljes gráf éleinek száma $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{n}{2}\right)=\frac{n\left(n-1\right)}{2}\mathrm{.}}\end{array}$ Ebből a teljes gráfból törlünk 21 élet úgy, hogy a kapott gráf pontjainak száma változatlan, azaz $n$ marad. A feladat szövege szerint a 21 él törlésével fagráfot kapunk, amely gráf éleinek száma $n-1$, ezért felírható, hogy $\begin{array}{c}{\displaystyle \frac{n\left(n-1\right)}{2}-21=n-1.}\end{array}$ Rendezéssel az $n^2-3n-40=0$ másodfokú egyenletet kapjuk, amelynek megoldásai $n_1=8$, $n_2=-5$. Nyilvánvaló, hogy $n_2=-5$ nem megoldása a feladatnak. Az egyetlen megoldás tehát $n=8$. Ellenőrizhető, hogy a 8 pontú teljes gráfnak 28 éle van, ebből 21-et törölve egy 7 élű gráfot kapunk. Ez önmagában nem biztos, hogy fagráf, de megadható a 8 pontú teljes gráf 21 olyan élének törlése, amelyre a megmaradt gráf fa, ahogy azt az ábrán láthatjuk. 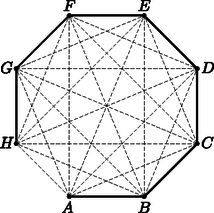    A törölt éleket szaggatottan, a megmaradt 7 élt folytonos vonallal ábrázoltuk. $c)$ A ${11}^n+{60}^n\le {61}^n$ egyenlőtlenség $n=1$-re valóban nem teljesül, mert ekkor $11+60>61$. Ha $n=2$, akkor az egyenlőtlenség teljesül, pontosabban az egyenlőség esete áll fenn, mert ${11}^2+{60}^2={61}^2$, a $\left(11;60;61\right)$ pitagoraszi számhármas. Legyen most $n>2$ és bizonyítsunk teljes indukcióval. Tegyük föl tehát a $k>2$ pozitív egész számra, hogy $\begin{array}{c}{\displaystyle {11}^k+{60}^k\le {61}^k\mathrm{.}}\end{array}$ Bizonyítani fogjuk az indukciós feltevés alkalmazásával, hogy az egyenlőtlenség $k+1$-re is fennáll. Mivel $\begin{array}{c}{\displaystyle {11}^{k+1}+{60}^{k+1}=11\cdot {11}^k+60\cdot {60}^k<60\cdot {11}^k+60\cdot {60}^k\mathrm{,}}\end{array}$ ezért $\begin{array}{c}{\displaystyle {11}^{k+1}+{60}^{k+1}<60\cdot \left({11}^k+{60}^k\right)\mathrm{.}}\end{array}$ Az indukciós feltevés miatt ${11}^k+{60}^k\le {61}^k$, így $60\cdot \left({11}^k+{60}^k\right)\le 60\cdot {61}^k$. Ugyanakkor nyilvánvaló, hogy $60\cdot {61}^k<61\cdot {61}^k={61}^{k+1}$. Az egyenlőtlenség tehát $n=k$-ból következik $n=\left(k+1\right)$-re, és mivel $n=2$-re igaz, ezért az állítás minden $n\ge 2$ pozitív egész számra fennáll.   II. rész     5. $a)$ Bizonyítsuk be, hogy a $2014\cdot 2016\cdot 2024\cdot 2026+100$ négyzetszám és állapítsuk meg, hogy melyik pozitív egész számnak a négyzete. (4 pont) $b)$ Igazoljuk, hogy a $\left]11\mathrm{,}5;\infty \right[$ számhalmazon értelmezett $\begin{array}{c}{\displaystyle f\left(x\right)=\sqrt[]{2x+28+10\cdot \sqrt[]{2x+3}}-\sqrt[]{2x+28-10\cdot \sqrt[]{2x+3}}}\end{array}$ függvény értéke állandó. Határozzuk meg ezt az állandó értéket. (5 pont) $c)$ Hány valós megoldása van a $\begin{array}{c}{\displaystyle \text{sin}{}^{4}x+\text{cos}{}^{4}x-\frac{5}{2}\cdot \text{sin}x\cdot \text{cos}x=\frac{1}{4}}\end{array}$ egyenletnek a $]-\frac{3\pi }{4};\frac{5\pi }{4}]$ számhalmazon? Adjuk meg a feltételeknek megfelelő összes megoldást. (7 pont)   Megoldás. $a)$ Legyen $a=2020$. Ezzel a $2014\cdot 2016\cdot 2024\cdot 2026+100$ számot átírhatjuk: $\begin{array}{c}{\displaystyle \left(a-6\right)\cdot \left(a-4\right)\cdot \left(a+4\right)\cdot \left(a+6\right)+\mathrm{100,}}\end{array}$ vagy másként $\begin{array}{c}{\displaystyle \left(a-6\right)\cdot \left(a+6\right)\cdot \left(a-4\right)\cdot \left(a+4\right)+100.}\end{array}$ Nevezetes azonosság alkalmazásával $\begin{array}{c}{\displaystyle \left(a^2-36\right)\cdot \left(a^2-16\right)+100=a^4-52a^2+676.}\end{array}$ Ugyanakkor $\begin{array}{c}{\displaystyle a^4-52a^2+676={\left(a^2-26\right)}^2\mathrm{.}}\end{array}$ Eszerint $2014\cdot 2016\cdot 2024\cdot 2026+100$ valóban négyzetszám, mégpedig $\begin{array}{c}{\displaystyle 2014\cdot 2016\cdot 2024\cdot 2026+100={\left({2020}^2-26\right)}^2={4080374}^2\mathrm{.}}\end{array}$ $b)$ A megadott $\left]11\mathrm{,}5;\infty \right[$ értelmezési tartomány miatt nyilvánvaló, hogy $2x+3>0$, továbbá $2x+28+10\cdot \sqrt[]{2x+3}>0$. Ugyanakkor a $\begin{array}{c}{\displaystyle 2x+28-10\cdot \sqrt[]{2x+3}\ge 0}\end{array}$ egyenlőtlenség is teljesül. Ezt a $\left]11\mathrm{,}5;\infty \right[$ számhalmaz figyelembe vételével végzett ekvivalens átalakításokkal beláthatjuk, mert ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2x+28}& {\displaystyle \ge 10\cdot \sqrt[]{2x+3}\mathrm{,}}\hfill \\ \hfill {\displaystyle x+14}& {\displaystyle \ge 5\cdot \sqrt[]{2x+3}\mathrm{,}}\hfill \\ \hfill {\displaystyle x^2+28x+196}& {\displaystyle \ge 25\cdot \left(2x+3\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle x^2-22x+121}& {\displaystyle \ge \mathrm{0,}}\hfill \\ \hfill {\displaystyle {\left(x-11\right)}^2}& {\displaystyle \ge \mathrm{0,}}\hfill \end{array}}$ ez pedig minden valós számra igaz. Egyenlőség csak $x=11$ esetén állhatna fenn, de mivel $x\in \left]11\mathrm{,}5;\infty \right[$, ezért ${\left(x-11\right)}^2>0$, és így $2x+28-10\cdot \sqrt[]{2x+3}>0$ is érvényes. Ez pedig azt jelenti, hogy az $f\left(x\right)$ függvényben szereplő minden négyzetgyökös kifejezés értelmezve van. Könnyen észrevehető, hogy $\begin{array}{c}{\displaystyle 2x+28+10\cdot \sqrt[]{2x+3}={\left(5+\sqrt[]{2x+3}\right)}^2}\end{array}$ és $\begin{array}{c}{\displaystyle 2x+28-10\cdot \sqrt[]{2x+3}={\left(5-\sqrt[]{2x+3}\right)}^2\mathrm{.}}\end{array}$ Ebből a ${\sqrt[]{a}}^2=|a|$ azonosság szerint az következik, hogy $\begin{array}{c}{\displaystyle f\left(x\right)=|5+\sqrt[]{2x+3}|-|5-\sqrt[]{2x+3}|\mathrm{.}}\end{array}$ A feltétel szerint $x>11\mathrm{,}5$, ebből azt kapjuk, hogy $2x+3>26>25$, és így a $\sqrt[]{2x+3}$ függvény szigorúan monoton növekvő tulajdonsága miatt $\sqrt[]{2x+3}>5$, ebből pedig azonnal adódik, hogy $5-\sqrt[]{2x+3}<0$. Mivel pedig $5+\sqrt[]{2x+3}>0$ nyilván igaz, ezért az abszolútérték értelmezése szerint ez azt jelenti, hogy $\begin{array}{c}{\displaystyle f\left(x\right)=5+\sqrt[]{2x+3}-\left(-5+\sqrt[]{2x+3}\right)=10.}\end{array}$ Ha tehát $x>11\mathrm{,}5$, akkor az $f\left(x\right)$ függvény értéke valóban állandó és ennek az állandónak az értéke 10. $c)$ Az egyenlet algebrai azonosság segítségével átalakítható: $\begin{array}{c}{\displaystyle {\left(\text{sin}{}^{2}x+\text{cos}{}^{2}x\right)}^2-2\cdot \text{sin}{}^{2}x\cdot \text{cos}{}^{2}x-\frac{5}{2}\cdot \text{sin}x\cdot \text{cos}x=\frac{1}{4}\mathrm{.}}\end{array}$ Mivel minden valós $x$-re $\text{sin}{}^{2}x+\text{cos}{}^{2}x=1$, ezért $\begin{array}{c}{\displaystyle 1-2\cdot \text{sin}{}^{2}x\cdot \text{cos}{}^{2}x-\frac{5}{2}\cdot \text{sin}x\cdot \text{cos}x=\frac{1}{4}\mathrm{,}}\end{array}$ illetve $4$-gyel való szorzás és rendezés után $\begin{array}{c}{\displaystyle 8\cdot \text{sin}{}^{2}x\cdot \text{cos}{}^{2}x+10\cdot \text{sin}x\cdot \text{cos}x-3=0.}\end{array}$ Bevezetjük a $\text{sin}\left(2x\right)=2\cdot \text{sin}x\cdot \text{cos}x$ trigonometriai azonosságból adódó $\text{sin}\left(2x\right)=y$ helyettesítést. Ezzel a $2y^2+5y-3=0$ másodfokú egyenletet kapjuk, amelynek gyökei $y_1=0\mathrm{,}5$ és $y_2=-3$. A második gyök nem ad megoldást a feladatra, hiszen $-1\le \text{sin}\left(2x\right)\le 1$. A $\text{sin}\left(2x\right)=0\mathrm{,}5$ egyenletből adódik, hogy $\begin{array}{c}{\displaystyle 2x=\frac{\pi }{6}+k\cdot 2\pi \mathrm{,}2x=\frac{5\pi }{6}+l\cdot 2\pi ;}\end{array}$ illetve $\begin{array}{c}{\displaystyle x=\frac{\pi }{12}+k\cdot \pi \mathrm{,}x=\frac{5\pi }{12}+l\cdot \pi \left(k;l\in \text{Z}\right)\mathrm{.}}\end{array}$ A kapott végtelen sok valós szám közül nem mindegyik esik a $\begin{array}{c}{\displaystyle \left]-\frac{3\pi }{4};\frac{5\pi }{4}\right]=\left]-\frac{9\pi }{12};\frac{15\pi }{12}\right]}\end{array}$ számhalmazba, ezért nem mindegyik megoldása a feladatnak. Egyszerű számolással beláthatjuk, hogy a $k=0$ és $k=1$, valamint $l=-1$ és $l=0$ egész számok megfelelő megoldást adnak, ekkor az egyenlet gyökei rendre $\begin{array}{c}{\displaystyle x_1=\frac{\pi }{12}\mathrm{,}{x}_2=\frac{13\pi }{12}\mathrm{,}{x}_3=-\frac{7\pi }{12}\mathrm{,}{x}_4=\frac{5\pi }{12}\mathrm{.}}\end{array}$ Az egyenletnek tehát a megadott intervallumban 4 valós megoldása van.   6. Az $AB$ szakasz felezőpontja $O$, az $A$ ponthoz közelebbi negyedelőpontja $C$, a $B$ ponthoz közelebbi negyedelőpontja $D$. A $C$, $O$, $D$ pontokban az $AB$ szakaszra rajzolt merőlegesek az $AB$ átmérőjű félkört rendre a $P$, $Q$, $R$ pontokban metszik. $a)$ Határozzuk meg a $BQP$ és $BRQ$ háromszögek szögeit. (8 pont) $b)$ Hány százaléka a $BRQP$ négyszög területe az $ABP$ háromszög területének? (Az eredményt két tizedesjegyre kerekítve adjuk meg.) 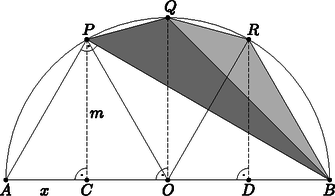(8 pont)   Megoldás. $a)$ Készítünk a feladat szövegének megfelelő rajzot, amelyen az $ABP$ derékszögű háromszög $P$-hez tartozó magasságát $m$-mel, az $AC$ szakasz hosszát $x$-szel jelöltük. Ekkor nyilvánvaló, hogy a feltételek miatt $CO=OD=DB=x$ és így $BC=3x$.     Thalész tétele miatt $APB={90}^{\circ }$. Az $ABP$ derékszögű háromszögben felírt magasságtétel szerint: $\begin{array}{c}{\displaystyle m^2=x\cdot 3x=3x^2\mathrm{.}}\end{array}$ (1) A $PAC$ derékszögű háromszögre érvényes a Pitagorasz-tétel: $x^2+m^2={PA}^2$, ahonnan (1) felhasználásával azonnal adódik, hogy ${PA}^2=4x^2$, és ezért $PA=2x$. Az $AB$ szakasz, mint átmérő fölé írt félkör középpontja $O$, ezért $OA=OP=2x$. Ebből, és a $PA=2x$ eredményből az következik, hogy az $OPA$ háromszög szabályos, és így $PAB\sphericalangle ={60}^{\circ }$, illetve $ABP\sphericalangle ={30}^{\circ }$. Az ábrán az $A$, $B$, valamint a $P$, $R$ és $C$, $D$ pontpárok az $OQ$ egyenesre szimmetrikusan helyezkednek el, ezért az $OPA$, $ORB$, illetve $OQP$, $OQR$, valamint $OPC$, $ORD$ háromszögek rendre egybevágók. Ebből adódik, hogy $POR\sphericalangle ={60}^{\circ }$, ez a $Q$ pontot is tartalmazó $PR$ ívhez tartozó középponti szög, így a középponti és kerületi szögek összefüggése alapján $PBR\sphericalangle ={30}^{\circ }$; mivel azonban a $PQ$ és $QR$ ívek hossza a szimmetria miatt egyenlő, ezért $\begin{array}{c}{\displaystyle PBQ\sphericalangle =QBR\sphericalangle ={15}^{\circ }\mathrm{.}}\end{array}$ (2) Az $R$ pontot tartalmazó $QB$ ívhez tartozó középponti szög derékszög, ebből azt kapjuk, hogy $BPQ\sphericalangle ={45}^{\circ }$, tehát a (2) összefüggést is felhasználva a $BQP$ háromszög szögeinek nagysága: ${15}^{\circ }$, ${120}^{\circ }$, ${45}^{\circ }$. Az $ORB$ háromszög szabályos, tehát $BOR\sphericalangle ={60}^{\circ }$, a középponti és kerületi szögek összefüggése miatt így $BQR\sphericalangle ={30}^{\circ }$, vagyis a $BRQ$ háromszög szögeinek nagysága rendre: ${15}^{\circ }$, ${135}^{\circ }$, ${30}^{\circ }$. $b)$ Az $ABP$ háromszög területe egyszerűen kifejezhető az $x$ és $m$ segítségével, hiszen $\begin{array}{c}{\displaystyle T_{ABP}=\frac{AB\cdot CP}{2}=\frac{4x\cdot m}{2}=2x\cdot m\mathrm{.}}\end{array}$ (3) A $BRQP$ négyszög területét talán legegyszerűbb úgy kifejezni, hogy a $BRQPC$ ötszög területéből levonjuk a $BPC$ derékszögű háromszög területét. Az $OQPC$ és $OQRD$ egybevágó, derékszögű trapézok, amelyek területére érvényes, hogy $\begin{array}{c}{\displaystyle T_{OQPC}=T_{OQRD}=\frac{OQ+m}{2}\cdot x;}\end{array}$ és mivel $OQ=2x$, ezért $\begin{array}{c}{\displaystyle T_{OQPC}=T_{OQRD}=x^2+\frac{x\cdot m}{2}\mathrm{.}}\end{array}$ (4) A $BRD$ derékszögű háromszög területe pedig: $\begin{array}{c}{\displaystyle T_{BRD}=\frac{x\cdot m}{2}\mathrm{,}}\end{array}$ (5) illetve a $BPC$ derékszögű háromszög területe $\begin{array}{c}{\displaystyle T_{BPC}=\frac{3x\cdot m}{2}\mathrm{.}}\end{array}$ (6) A (4), (5), (6) összefüggések alapján a $BRQP$ négyszög területe: $\begin{array}{c}{\displaystyle T_{BRQP}=T_{OQPC}+T_{OQRD}+T_{BRD}-T_{BPC}=2x^2\mathrm{.}}\end{array}$ (7) (3) és (7) egybevetésével azt kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{T_{BRQP}}{T_{ABP}}=\frac{2x^2}{2x\cdot m}=\frac{x}{m}=\frac{1}{\sqrt[]{3}}\approx 0\mathrm{,}\mathrm{5774,}}\end{array}$ hiszen (1) szerint $m=x\cdot \sqrt[]{3}$. Eszerint a $BRQP$ négyszög területe az $ABP$ háromszög területének kb. 57,74 %-a.   7. Hány olyan $p$ pozitív prímszám van, amelyre nem igaz, hogy a $\begin{array}{c}{\displaystyle \left(p-2\right)\cdot x^2+\left(2p+3\right)\cdot x+p^2-1=0}\end{array}$ egyenletnek legfeljebb egy valós gyöke van? (16 pont)   Megoldás. Ha nem igaz, hogy a $\left(p-2\right)\cdot x^2+\left(2p+3\right)\cdot x+p^2-1=0$ egyenletnek legfeljebb egy valós megoldása van, akkor legalább két megoldásának kell lennie. Az egyenletben az $x$ változó második hatványon szerepel, így az egyenlet legfeljebb másodfokú. De elsőfokú nem lehet, mert az elsőfokú egyenletnek legfeljebb egy valós gyöke van. Ez éppen azt jelenti, hogy a $p=2$ prímszám nem megoldása a feladatnak, mert ekkor behelyettesítéssel a $7x+3=0$ egyenletet kapjuk. Ennek megoldása egyébként $x=-\frac{3}{7}$. Ha $p\ne 2$, akkor az egyenlet másodfokú. A fentiek szerint ennek pontosan két valós megoldása kell, hogy legyen (kettőnél több nyilván nem lehet). Ezért azokat a $p$ számokat keressük, amelyre az egyenlet diszkriminánsa pozitív. Felírva a diszkriminánst: $\begin{array}{c}{\displaystyle D={\left(2p+3\right)}^2-4\cdot \left(p-2\right)\cdot \left(p^2-1\right)>\mathrm{0,}}\end{array}$ amelyből a műveletek elvégzésével és rendezéssel a $\begin{array}{c}{\displaystyle 4p^3-12p^2-16p<1}\end{array}$ (1) egyenlőtlenséget kapjuk. Vizsgáljuk a továbbiakban az $f\left(p\right)=4p^3-12p^2-16p$ harmadfokú függvényt. Először keressük meg a függvény zérushelyeit (eltekintve egyelőre attól, hogy $p$ pozitív prím). Szorzattá alakítással: $\begin{array}{c}{\displaystyle f\left(p\right)=4p\cdot \left(p^2-3p-4\right)\mathrm{,}}\end{array}$ ebből azt kapjuk, hogy $f\left(p\right)$ zérushelyei $p_1=-1$, $p_2=0$, $p_3=4$. Az $f\left(p\right)=4p\cdot \left(p^2-3p-4\right)$ függvényt szorzat alakba írva az egyenlőtlenség: $\begin{array}{c}{\displaystyle 4p\cdot \left(p+1\right)\cdot \left(p-4\right)<1.}\end{array}$ Ezt az egyenlőtlenséget kell a feltételek figyelembe vételével megoldani. Mivel $p$ pozitív prím, ezért a szorzatban $4p$ és $\left(p+1\right)$ is $\text{1}$-nél nagyobb egész szám. A $\left(p-4\right)$ tényező $p=2$ és $p=3$ esetén negatív, így a bal oldal negatív, tehát kisebb, mint 1. A $p=5$, vagy annál nagyobb prímekre a $\left(p-4\right)$ szorzótényező is pozitív egész szám, így a szorzat 1-nél nagyobb lesz. Az egyenlőtlenség tehát csak a $p=2$ és $p=3$ prímszámokra teljesül. A $p=2$ esetet már kizártuk, ezért $p=3$ az egyetlen megoldás. A $p=3$ értékre az eredeti egyenlet $\begin{array}{c}{\displaystyle x^2+9x+8=\mathrm{0,}}\end{array}$ ennek valóban két gyöke van, mégpedig $x_1=-1$, $x_2=-8$.   Megjegyzés. A $p=3$ megoldást más módon is megtalálhatjuk. Meghatározzuk az $f\left(p\right)$ differenciálhányadosát: $\begin{array}{c}{\displaystyle f\text{'}\left(p\right)=12p^2-24p-16=4\cdot \left(3p^2-6p-4\right)\mathrm{.}}\end{array}$ Az $f\text{'}\left(p\right)$ függvény zérushelyei: $\begin{array}{c}{\displaystyle p_1\text{'}=\frac{3-\sqrt[]{21}}{3}\approx -0\mathrm{,}528;p_2\text{'}=\frac{3+\sqrt[]{21}}{3}\approx 2\mathrm{,}528.}\end{array}$ Az $f\text{'}\left(p\right)$ másodfokú függvény ezeken a helyeken előjelet vált, ezért $p_1\text{'}$ és $p_2\text{'}$ az $f\left(p\right)$ szélsőértékhelyei. Most figyelembe vesszük, hogy $p$ pozitív prím. Eszerint az $f\left(p\right)$ függvényt nem vizsgáljuk a $p<p_1\text{'}$ intervallumon, noha a $p_1\text{'}$ helyen szélsőértéke van, és így előfordulhat, hogy (1) valamilyen negatív $p$ számra fennáll. Nem szükséges vizsgálni az $f\left(p\right)$ függvényt a $\left]p_1\text{'};p_2\text{'}\right[$ halmazon sem, mert ebben az intervallumban csak a $p=2$ prímszám fordul elő, ez pedig, mint láttuk, nem megoldása a feladatnak. A $p_2\text{'}$ helyen az $f\text{'}\left(p\right)$ másodfokú függvény negatívból pozitívba megy át, ezért itt $f\left(p\right)$ csökkenő függvényből növekvőbe megy át. Ez pedig azt jelenti, hogy elegendő vizsgálni az (1) egyenlőtlenség teljesülését a $p>p_2\text{'}$ prímszámokra. Az első ilyen prím a $p=3$. Behelyettesítéssel ellenőrizhetjük, hogy ekkor (1) bal oldalának értéke $-48$, erre nyilván fennáll (1), tehát $p=3$ megoldása a feladatnak. A következő prím $p=5$, erre (1) bal oldalának értéke 120, vagyis erre (1) nem teljesül, és így $p=5$ nem megoldás. A $p>5$ prímszámokat már nem szükséges vizsgálnunk, hiszen itt $f\left(p\right)$ növekvő, tehát biztosan $120$-nál nagyobb értéket kapnánk egy következő prím behelyettesítésekor. A $p>5$ prímszámok tehát nem megoldásai a feladatnak, így az egyetlen megoldás $p=3$.   8. Egy kocka minden élének hossza $n$, ahol $n$ pozitív egész szám. A kocka minden lapját fehérre festjük, majd a kockát a lapjaival párhuzamos síkok mentén $n^3$ darab egységnyi élű kockára daraboljuk. $a)$ Hányszorosa a kis kockák felszínének összege az eredeti kocka felszínének? (2 pont) Ezután az összes kis kocka lapjait megszámozzuk a következő szabály szerint: először azoknak a kis kockáknak a $6$-$6$ lapját számozzuk meg a pozitív egész számokkal $1$-től kiindulva, amelyeknek egyetlen lapja sem fehér, ezután a számozást folytatjuk azon kis kockák lapjaival, amelynek egy oldala fehér, utána a két fehér lappal rendelkező kis kockák következnek, végül azok a kis kockák, amelyeknek három lapja fehér. Ezzel az eljárással elérjük, hogy minden kis kocka minden lapján szerepel egy-egy pozitív egész szám és ezek a számok mind különbözők. $b)$ Legalább mekkora az $n$ szám, ha biztosan tudjuk, hogy a $2020$ szám olyan kis kockára kerül, amelynek nincs fehérre festett lapja? (4 pont) $c)$ Határozzuk meg a pozitív egész $n$ számot, ha a fenti számozással a $4326$ szám az utolsó olyan kis kocka utoljára megszámozott egyik lapjára kerül, amelynek pontosan két lapja fehér. (6 pont) $d)$ Az $n^3$ számú kis kockából véletlenszerűen kiválasztunk egy darabot. Mennyi annak az esélye, hogy a kiválasztott kis kockának legalább az egyik lapja fehér, ha $n=8?$ (4 pont)   Megoldás. $a)$ Az eredeti kocka felszíne $6n^2$, az $n^3$ darab egységkocka felszínének összege pedig $6n^3$, ez éppen $n$-szerese az eredeti kocka felszínének. $b)$ Az $n$ élű kockát úgy tudjuk a lapjaival párhuzamos élű síkokkal $n^3$ darab egységkockára darabolni, ha három, egymásra merőleges élét egyenként $n-1$, az adott élre merőleges síkkal elvágjuk az ábrának megfelelően (a 3 kiválasztott élet szaggatottan ábrázoltuk). 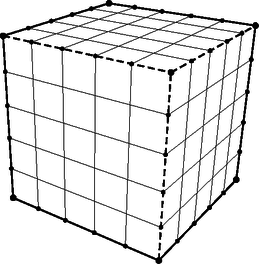    Az ábra azt is megmutatja, hogy a kis kockák közül éppen 8-nak lesz három lapja befestve (a kocka 8 csúcsánál), pontosan két lapját olyan kis kockáknak festjük be, amelyek az eredeti kocka élei mentén helyezkednek el, de egyetlen csúcsuk sem esik egybe az eredeti kocka valamelyik csúcsával, ebből pedig a nagy kocka 12 éle mentén összesen $12\cdot \left(n-2\right)$ van. Innen azt is láthatjuk, hogy egy lapjával befestett kis kocka éppen $6\cdot {\left(n-2\right)}^2$ darab lesz, olyan kis kocka pedig, amelynek egyetlen lapja sincs befestve, pontosan ${\left(n-2\right)}^3$. Most már válaszolhatunk a $b)$ feladat kérdésére is. Számozási feltételeink figyelembevételével ugyanis azt kapjuk, hogy $\begin{array}{c}{\displaystyle 6\cdot {\left(n-2\right)}^3\ge \mathrm{2020,}\text{azaz}n-2\ge \sqrt[3]{\frac{2020}{6}}\approx 6\mathrm{,}96.}\end{array}$ Ebből az következik, hogy $n\ge 8\mathrm{,}96$, tehát $n$ értéke legalább 9. $c)$ A $b)$ feladat megoldásánál már láttuk, hogy olyan kis kocka, amelynek egyetlen lapja sem fehér, ${\left(n-2\right)}^3$ darab van, ezek számozására összesen az első $6\cdot {\left(n-2\right)}^3$ pozitív egész számot használtuk fel. Olyan kocka pedig, amelynek egy lapja fehér, $6\cdot {\left(n-2\right)}^2$ darab van, ezek számozására a következő $6\cdot 6\cdot {\left(n-2\right)}^2$ számot használtuk, végül $12\cdot \left(n-2\right)$ olyan kis kocka van, amelynek pontosan két lapja fehér. Ezen kockák lapjaihoz a számozási szabály szerint ezután következő $6\cdot 12\cdot \left(n-2\right)$ darab pozitív egész számot használtuk. Felírható a következő egyenlet: $\begin{array}{c}{\displaystyle 6\cdot {\left(n-2\right)}^3+36\cdot {\left(n-2\right)}^2+72\cdot \left(n-2\right)=\mathrm{4326,}}\end{array}$ 6-tal való osztás után $\begin{array}{c}{\displaystyle {\left(n-2\right)}^3+6\cdot {\left(n-2\right)}^2+12\cdot \left(n-2\right)=721.}\end{array}$ (1) Az (1) egyenlet az $n-2=x$ helyettesítéssel átírható: $\begin{array}{c}{\displaystyle x^3+6x^2+12x=\mathrm{721,}}\end{array}$ illetve $\begin{array}{c}{\displaystyle x\cdot \left(x^2+6x+12\right)=721.}\end{array}$ (2) A (2) egyenlet bal oldalának mindkét szorzótényezője pozitív egész. Az $x$ osztója a $721$-nek, amelynek prímtényezős felbontása $721=7\cdot 103$, tehát $x$ lehetséges értékei 1; 7; 103; 721. Nyilván $x=1$ nem értelmezhető a feladat szempontjából, ezért csak a maradék 3 számot kell megvizsgálnunk. Egyszerű számolással kapjuk, hogy csak $x=7$ a megoldás, mert a többi értékre a (2) egyenlet zárójeles tényezője 721-nél nagyobb lesz. A megoldás tehát az $n-2=7$, azaz $n=9$. $d)$ Ha $n=8$, akkor az előzőek szerint ${\left(8-2\right)}^3=216$ kis kocka lapjai nincsenek befestve, $6\cdot {\left(8-2\right)}^2$ darab kis kockának pontosan egy lapja fehér, $12\cdot \left(8-2\right)=72$ kis kockának pontosan két lapja van befestve, végül $8$ kis kockának pontosan három lapja fehér, ez összesen $8^3=512$ darab kis kocka. A komplementer esemény valószínűségével számolunk, vagyis annak valószínűségét keressük, hogy a kiválasztott kocka egyetlen lapja sem fehér. Ekkor a kedvező esetek száma az előzőek szerint $k=216$, az összes eset száma nyilván $n^3=512$. Ezért $\begin{array}{c}{\displaystyle P\left(\overline{A}\right)=\frac{216}{512}=\frac{27}{64}\mathrm{,}}\end{array}$ és így a feladat megoldása $\begin{array}{c}{\displaystyle P\left(A\right)=1-\frac{27}{64}=\frac{37}{64}\mathrm{.}}\end{array}$   9. Az $ABC$ háromszög csúcsainak koordinátái a derékszögű koordináta-rendszerben $A\left(0;-2\right)$, $B\left(6;10\right)$, $C\left(-3;1\right)$. $a)$ Bizonyítsuk be, hogy az $ABC$ derékszögű háromszög. (3 pont) $b)$ Igazoljuk, hogy az $y=-x^2+8x-10$ egyenletű parabolának a $BC$ oldal egyenesével nincs közös pontja, de az $AB$ oldal egyenesével két közös pontja is van. Határozzuk meg az $AB$ oldal egyenese és az $y=-x^2+8x-10$ egyenletű parabola metszéspontjainak koordinátáit. (5 pont) $c)$ Számítsuk ki, hogy az $ABC$ háromszög területének hányadrészét fedik le azok a pontok, amelyekre $y\le -x^2+8x-1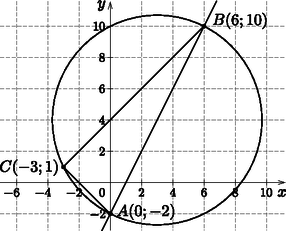0$ teljesül. (8 pont)   Megoldás. $a)$ I. megoldás. Ábrázoljuk a pontokat a derékszögű koordináta-rendszerben, amelyben megrajzoltuk a háromszög körülírt körét is. Az ábra alapján az a sejtésünk alakulhat ki, hogy az $ABC$ háromszög derékszögű csúcsa a $C$ pontban van.     Kiszámítjuk a ${\overrightarrow{v}}_{CA}$ és ${\overrightarrow{v}}_{CB}$ vektorok koordinátáit a végpontok és a közös kezdőpont koordinátáinak különbségeként: ${\overrightarrow{v}}_{CA}\left(3;-3\right)$ és ${\overrightarrow{v}}_{CB}\left(9;9\right)$. A két vektor skaláris szorzata felírható a megfelelő koordináták szorzatának összegeként: $\begin{array}{c}{\displaystyle {\overrightarrow{v}}_{CA}\cdot {\overrightarrow{v}}_{CB}=3\cdot 9+\left(-3\right)\cdot 9=0.}\end{array}$ Két vektor skaláris szorzata akkor és csak akkor zérus, ha a két vektor merőleges egymásra. Ez éppen azt jelenti, hogy $CA$ merőleges $CB$-re, vagyis az $ABC$ háromszög $C$ csúcsnál levő belső szöge valóban derékszög.   II. megoldás. Kiszámítjuk az $AB$, $BC$ és $CA$ oldalak hosszát: $\begin{array}{c}{\displaystyle AB=\sqrt[]{6^2+{12}^2}=\sqrt[]{180}\mathrm{,}BC=\sqrt[]{9^2+9^2}=\sqrt[]{162}\mathrm{,}CA=\sqrt[]{3^2+{\left(-3\right)}^2}=\sqrt[]{18}\mathrm{.}}\end{array}$ Mivel ${BC}^2+{CA}^2={\sqrt[]{162}}^2+{\sqrt[]{18}}^2={\sqrt[]{180}}^2={AB}^2$, ezért a Pitagorasz-tétel megfordítása alapján az $ABC$ háromszögben a $C$ csúcsnál levő belső szög valóban derékszög.   $b)$ Felírjuk a $BC$ és az $AB$ oldalak egyeneseinek egyenletét. Mivel már tudjuk, hogy ${\overrightarrow{v}}_{CB}\left(9;9\right)$ vagy ${\overrightarrow{v}}_{CB}\left(1;1\right)$, ezért a $BC$ oldal irányvektoros egyenletét felírva $x-y=-4$. Az $AB$ oldal egy irányvektora ${\overrightarrow{v}}_{AB}\left(6;12\right)$, vagy ${\overrightarrow{v}}_{AB}\left(1;2\right)$, ezért az $AB$ oldal egyenlete $2x-y=2$. Keressük először az $x-y=-4$, $y=-x^2+8x-10$ másodfokú egyenletrendszer megoldásait. Behelyettesítéssel: $x-\left(-x^2+8x-10\right)=-4$, ahonnan $x^2-7x+14=0$. Ennek az egyenletnek nincs valós megoldása, mert a diszkriminánsa $D=-7$. Ez azt jelenti, hogy az $y=-x^2+8x-10$ parabolának a $BC$ oldal egyenesével valóban nincs közös pontja. Az $2x-y=2$, $y=-x^2+8x-10$ másodfokú egyenletrendszer megoldása: $\begin{array}{c}{\displaystyle 2x-\left(-x^2+8x-10\right)=\mathrm{2,}\text{innen}{x}^2-6x+8=0.}\end{array}$ Az egyenlet megoldásai az $x_1=2$ és $x_2=4$ valós számok. Visszahelyettesítve megkapjuk az $AB$ egyenes és a parabola közös pontjait: $D\left(2;2\right)$, $E\left(4;6\right)$. $c)$ Ábrázoljuk együtt a koordinátarendszerben a háromszöget és a parabolát, a besatírozott rész területét akarjuk kiszámítani. 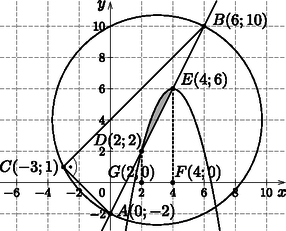    Mivel a $BC$ egyenesének és a parabolának nincs közös pontja, ezért a $BC$ egyenes a parabola fölött helyezkedik el. Az $ABC$ háromszög területe: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{ABC}}& {\displaystyle =\frac{BC\cdot CA}{2}=\frac{\sqrt[]{162}\cdot \sqrt[]{18}}{2}=27\left(\text{területegység}\right)\mathrm{.}}\hfill \end{array}}$ A parabola alatti területnek az $x_1=2$ és $x_2=4$ határok közé eső része a Newton‐Leibniz-formula alkalmazásával: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_1}& {\displaystyle ={\int }_2^4\left(-x^2+8x-10\right)\text{d}x={\left[-\frac{x^3}{3}+4x^2-10x\right]}_2^4=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(-\frac{64}{3}+64-40\right)-\left(-\frac{8}{3}+16-20\right)=\frac{28}{3}\mathrm{.}}\hfill \end{array}}$ Az ábrán a $DEFG$ trapéz területe: $T_2=\frac{DG+EF}{2}\cdot FG=\frac{2+6}{2}\cdot 2=8\left(\text{területegység}\right)$. A szürkített területet a $T_1$ és $T_2$ területek különbségeként kapjuk: $\begin{array}{c}{\displaystyle T=T_1-T_2=\frac{28}{3}-8=\frac{4}{3}\left(\text{területegység}\right)\mathrm{.}}\end{array}$ Ebből az következik, hogy $\begin{array}{c}{\displaystyle \frac{T}{T_{ABC}}=\frac{\frac{4}{3}}{27}=\frac{4}{81}\mathrm{,}}\end{array}$ tehát a szürkített terület az $ABC$ háromszög területének pontosan $\frac{4}{81}$-ed része.    Bíró Bálint (Eger)