Kezdőlap


Cím:	Beszámoló a 2020. évi Eötvös-versenyről
Szerző(k):	Tichy Géza , Vankó Péter , Vigh Máté
Füzet:	2020/december, 558 - 563. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Beszámoló a 2020. évi Eötvös-versenyről

Az Eötvös Loránd Fizikai Társulat 2020. évi Eötvös-versenye október 9-én délután 3 órai kezdettel tizennégy magyarországi helyszínen^{$^{*}$} került megrendezésre. Ezért külön köszönettel tartozunk mindazoknak, akik ebben szervezéssel, felügyelettel a segítségünkre voltak. A versenyen a három feladat megoldására 300 perc áll rendelkezésre, bármely írott vagy nyomtatott segédeszköz használható, de (nem programozható) zsebszámológépen kívül minden elektronikus eszköz használata tilos. Az Eötvös-versenyen azok vehetnek részt, akik vagy középiskolai tanulók, vagy a verseny évében fejezték be középiskolai tanulmányaikat. Összesen 48 versenyző adott be dolgozatot, 11 egyetemista és 37 középiskolás.
Ismertetjük a feladatokat és azok megoldását.

*

1. feladat. Egy

m_{0}

tömegű, állandó

c

fajhőjű minta hőmérséklete kicsivel a nitrogén

T_{0}

forráspontja alatt van. Rendelkezésünkre áll

m

tömegű, forrásban lévő folyékony nitrogén és egy hőszivattyú. Mekkora minimális hőmérsékletre lehet lehűteni a mintát, mire elforr az összes nitrogén? A nitrogén forráshője

L

Megoldás. Egy

η = \frac{T_{2} - T_{1}}{T_{2}}

hatásfokú, hőerőgépként üzemeltetett Carnot-féle körfolyamat esetén a felső hőtartályból kivett hő

η

-ad része mint munkavégzés jelenik meg,

(1 - η)

-ad része pedig az alsó hőtartályba kerül. Hőszivattyúként üzemeltetve munkát kell befektetnünk, az alsó hőtartályból szivattyúzzuk át az energiát a felsőbe, azaz a hő előjele változik ellenkezőre.
A Carnot-körfolyamattal általában úgy találkozunk, hogy a gép két állandó hőmérsékletű hőtartály között működik. Feladatunkban a Carnot-gép felső hőtartálya a forrásban lévő nitrogén, amelynek hőmérséklete végig

T_{0}

, az alsó hőtartály pedig a minta, amely viszont lassan hűl,

T

hőmérséklete nem állandó. Egy ciklus során azonban a minta hőmérséklete állandónak tekinthető.
Ebből a lassan változó hőmérsékletű hőtartályból vonunk el egy kis lépésben

c m_{0} Δ T

hőt. Ez a hő a felső hőtartályba érkező

q

hőnek

\begin{matrix} 1 - η = 1 - \frac{T_{0} - T}{T_{0}} = \frac{T}{T_{0}} -szorosa, \end{matrix}

ahogy az 1. ábrán is látható.

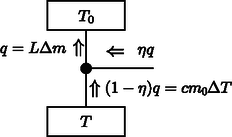1. ábra

Δ m

mennyiségű nitrogén forrt el, akkor a felső hőtartálynak

L Δ m

hőt kellett kapnia. Ebből a

\begin{matrix} c m_{0} Δ T = \frac{T}{T_{0}} L Δ m \end{matrix}

összefüggéshez jutunk. Ez a

\begin{matrix} \frac{c m_{0} d T}{T} = \frac{L d m}{T_{0}} \end{matrix}

differenciális összefüggéséhez vezet. Ezt kell integrálni a kezdeti állapottól a végső állapotig. Az alsó hőtartály

T

hőmérséklete

T_{0}

-ról

T_{{min}_{}^{}}

-re csökken, és közben a folyékony nitrogén tömege

m

-ről nullára csökken. Tehát

\begin{matrix} c m_{0} ln \frac{T_{0}}{T_{{min}_{}^{}}} = \frac{L m}{T_{0}}, \end{matrix}

amiből a keresett minimális hőmérséklet

\begin{matrix} T_{{min}_{}^{}} = T_{0} e^{- \frac{L m}{T_{0} c m_{0}}} . \end{matrix}

Megjegyzés. Aki tudja, hogy a Carnot-körfolyamat közben az entrópia állandó, és ismeri az entrópia kifejezéseit, az azonnal megkapja az integrálásból kapott összefüggést.

2. feladat. Könnyen gördülő,

2 m

tömegű kiskocsira egy árbóc van rögzítve, aminek felső végére

ℓ

hosszúságú fonállal egy

m

tömegű kis golyót függesztettünk. A kiskocsit egy nem túl meredek,

α

hajlásszögű lejtőre helyezzük, majd megvárjuk az inga lengéseinek lecsillapodását, és végül a kocsit elengedjük (2. ábra).

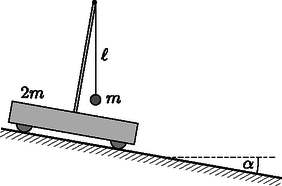2. ábra

a)

A mozgás során mennyire tér ki a fonál a függőlegestől?

b)

Mekkora utat tesz meg a kiskocsi, amíg a fonál újra függőlegessé válik?

Megoldás. Az ingából és kiskocsiból álló rendszerre lényegében csak a nehézségi erő és a lejtőre merőleges irányú kényszererők hatnak, hiszen a kerekek gyorsuló forgásához szükséges tapadási súrlódási erőt a ,,könnyen gördülő'' kifejezés miatt elhanyagolhatjuk. Lejtőirányú komponense csak a nehézségi erőnek van, ezért a rendszer tömegközéppontja a lejtővel párhuzamos irányban állandó,

g sin α

gyorsulással mozog. A tömegközéppont a mozgás során a lejtőre merőleges irányban is gyorsul, ez azonban a további gondolatmenet szempontjából nem lényeges.

Üljünk bele a zérus kezdősebességű, a lejtővel párhuzamosan

| a | = g sin α

nagyságú gyorsulással mozgó vonatkoztatási rendszerbe! Egy gyorsuló rendszerben bármely

m'

tömegű testre a Newton-törvények csak úgy maradnak érvényben, ha a valójában rá ható (kölcsönhatásból származó) erők mellett bevezetjük a rendszer

a

gyorsulásával ellentétes irányú,

- m' a

tehetetlenségi erőt is. A

- m' a

tehetetlenségi erő és az

m' g

nehézségi erő vektori összege

m' g^{*}

alakban is felírható, ahol

g^{*} = g - a

. A gyorsuló rendszerben tehát minden test úgy mozog, mintha egy

g^{*}

effektív nehézségi gyorsulású erőtérben helyezkedne el. Esetünkben a vonatkoztatási rendszer

a

gyorsulása éppen megegyezik a

g

nehézségi gyorsulás lejtőirányú összetevőjével, ezért az effektív

g^{*}

nehézségi gyorsulás a lejtőre merőleges irányú, nagysága pedig

g cos α

. Mivel a gyorsuló rendszerben

g^{*}

határozza meg a függőleges irányt, célszerű a feladat ábráját elforgatni, ahogy az a 3. ábrán is látható.

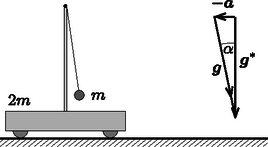3. ábra

A mozgást a gyorsuló vonatkoztatási rendszerünkben elemezve azt látjuk, hogy a kiskocsi és az ingatest nyugalomból indul, az inga kezdeti szögkitérése

g^{*}

irányától mérve jobbra éppen

α

. Az inga lengése során a rendszer tömegközéppontja külső lejtőirányú erő hiányában nem mozdul el, így mind a kiskocsi, mind pedig az ingatest mozgásba jön. A mechanikai energia megmaradásából és a tömegközéppont-tételből következik, hogy az inga szögkitérésének legnagyobb értéke

g^{*}

-hoz viszonyítva a túlsó oldalon szintén

α

lesz, ami akkor következik be, amikor a kiskocsi és az ingatest először áll meg. Ez azt jelenti, hogy az eredeti vonatkoztatási rendszerben az inga a kezdeti helyzetéhez képest (azaz

g

-hez viszonyítva) maximálisan

2 α

szöggel tér ki. Ezzel a feladat

a)

kérdésére válaszoltunk.

Térjünk most rá a

b)

részre. A gyorsuló rendszerben az ingatest és a kiskocsi is periodikus mozgást végez az egyensúlyi helyzet körül, amelyben az inga fonala éppen párhuzamos

g^{*}

-gal. Az inga legkorábban

T

periódusidő múlva érkezik vissza a kiindulási helyzetbe. Ebben a pillanatban a tömegközéppont elmozdulása

\begin{matrix} s = \frac{1}{2} g sin α \cdot T^{2}, \end{matrix}

és ugyanekkora a kocsi elmozdulása is, hiszen a kocsi relatív helyzete a tömegközépponthoz viszonyítva éppen ugyanaz, mint az indítási állapotban volt. Feladatunk tehát a rezgés

T

periódusidejének meghatározása.

A gyorsuló rendszerben a tömegközéppont megmaradása miatt a kocsi kitérése minden pillanatban feleakkora és ellentétes irányú, mint az ingatest lejtővel párhuzamos irányú kitérése. Ezért a fonál felső harmadolópontja lényegében nem mozdul el (valójában a lejtőre merőleges irányban mégis, de elhanyagolható mértékben). Az ingatest tehát úgy mozog a

| g^{*} | = g cos α

nehézségi gyorsulású erőtérben, mintha egy

2 ℓ / 3

hosszúságú fonálra lenne felfüggesztve. Egy ilyen inga lengésideje kis kitérések esetén:

\begin{matrix} T = 2 π \sqrt[]{\frac{2 ℓ}{3 g cos α}} . \end{matrix}

Vajon alkalmazható-e most ez az összefüggés? A feladat szövege szerint a lejtő nem túl meredek. Egy

45^{\circ}

-os lejtő már elég meredeknek számít, de az ekkora szögben kitérített inga lengésideje is csak kb. 4%-kal nagyobb a fenti képlettel számolt lengésidőnél. Ha a lejtő csak

30^{\circ}

-os, az eltérés 2%-nál is kisebb. Jó közelítéssel tehát azt mondhatjuk, hogy a kocsi elmozdulása addig a pillanatig, amíg az inga újra függőlegessé válik

\begin{matrix} s \approx \frac{1}{2} g sin α \cdot 4 π^{2} \frac{2 ℓ}{3 g cos α} = \frac{4 π^{2}}{3} ℓ tg α . \end{matrix}

3. feladat. Egy ideális diódából, két

R = 2

Ω

nagyságú ellenállásból, egy kezdetben töltetlen,

C = 100 μ

F kapacitású kondenzátorból és egy feszültséggenerátorból a 4. ábrán látható kapcsolást állítottuk össze. A feszültséggenerátoron

f = 5 kHz

frekvenciájú,

+ U_{0}

és

- U_{0}

között változó szimmetrikus négyszögjelet állítunk be, ahol

U_{0} = 3, 6 V

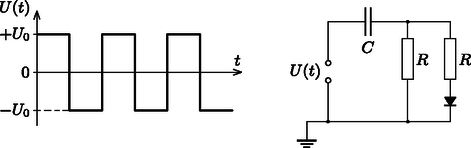4. ábra

a)

Mekkora maximális feszültségre töltődik fel a kondenzátor?

b)

A kondenzátor töltetlen állapotától számítva körülbelül mennyi idő után éri el a kondenzátor feszültsége a maximális érték felét?

Megoldás. A kapcsolásban félperiódusonként felváltva

+ U_{0}

és

- U_{0}

feszültséget kapcsolunk egy soros

R C

kapcsolásra, ahol a kondenzátor kapacitása mindvégig

C

, az ellenállás pedig az áramiránytól függően

R_{1} = \frac{R}{2}

, illetve

R_{2} = R

. Jól ismert, hogy ha egy töltetlen,

C

kapacitású kondenzátorból és egy

R

ellenállásból álló soros

R C

kapcsolásra

U_{0}

feszültséget kapcsolunk, akkor a kondenzátor feszültsége az

\begin{matrix} U (t) = U_{0} (1 - e^{- \frac{t}{τ}}) \end{matrix}

függvény szerint változik, ahol az időállandó

τ = R C

.
Vegyük észre, hogy a mi esetünkben az (egyik) időállandó

τ = R C = 0, 2

s (a másik ennek fele), a négyszögjel periódusideje pedig

T = \frac{1}{f} = 0, 2

ms, és így

T ≪ τ

. Emiatt egy fél periódusnyi idő alatt a töltődő kondenzátor feszültsége nagyon jó közelítéssel lineárisan változik.
Legyen a kondenzátor feszültsége egy adott időpillanatban

U_{C} (t)

, a kondenzátoron átfolyó áram pedig

I (t)

. A négyszögjel első fél periódusában (amikor a dióda nyitva van, és mindkét ellenálláson folyik áram)

\begin{matrix} U_{0} - U_{C} = R_{1} I_{1} (t) = \frac{R}{2} I_{1} (t), amiből I_{1} (t) = \frac{2}{R} [U_{0} - U_{C} (t)] . \end{matrix}

Egy fél periódus alatt ez az áram

I_{1} (t) \frac{T}{2}

töltést szállít a kondenzátorra, így a kondenzátor feszültségének megváltozása

\begin{matrix} Δ U_{C} (t) = \frac{1}{C} I_{1} (t) \frac{T}{2} = \frac{T}{R C} [U_{0} - U_{C} (t)] = \frac{T}{τ} [U_{0} - U_{C} (t)] . \end{matrix}

A másik fél periódusban (amikor a dióda lezár, és csak az egyik ellenálláson folyhat áram)

\begin{matrix} - U_{0} - U_{C} = R_{2} I_{2} (t) = R I_{2} (t), amiből I_{2} (t) = \frac{1}{R} [- U_{0} - U_{C} (t)], \end{matrix}

és a fél periódus alatt a kondenzátor feszültségének megváltozása

\begin{matrix} Δ U_{C} (t) = \frac{1}{C} I_{2} (t) \frac{T}{2} = \frac{T}{2 R C} [- U_{0} - U_{C} (t)] = \frac{T}{2 τ} [- U_{0} - U_{C} (t)] . \end{matrix}

Egy teljes periódus alatt a feszültség teljes megváltozása a két fél periódus alatti változás összege:

\begin{matrix} Δ U_{C} (t) = \frac{T}{2 τ} [U_{0} - 3 U_{C} (t)] = \frac{3 T}{2 τ} [\frac{U_{0}}{3} - U_{C} (t)] . \end{matrix}

A kondenzátor feszültsége akkor nem nő tovább, ha

Δ U_{C} (t) = 0

, azaz ha

U_{C} (t) = \frac{U_{0}}{3}

, tehát a kondenzátor hosszú idő után

U_{C} (\infty) = \frac{U_{0}}{3} = 1, 2

V feszültségre töltődik fel.

Ezután áttérünk a

b)

kérdés megválaszolására. Mivel a periódusidő sokkal kisebb az időállandónál, az egy periódus alatti feszültségváltozás nagyon kicsi, a kondenzátor sok perióduson át töltődik. Ezen az időskálán a félperiódusok alatti töltődések és kisülések kis ingadozása nem is látszik. Egy olyan folyamatot kapunk, ahol a kondenzátor feszültsége lényegében folyamatosan nő a kezdeti

U_{C} (0) = 0

értéktől az

U_{C} (\infty)

értékig.
Az utolsó egyenletünk alapján

\begin{matrix} \frac{d [U_{C} (\infty) - U_{C} (t)]}{d t} \approx \frac{Δ [U_{C} (\infty) - U_{C} (t)]}{T} = - \frac{3}{2 τ} [U_{C} (\infty) - U_{C} (t)] . \end{matrix}

Ez pedig egy ugyanolyan differenciálegyenlet, mint amely leírja egy kondenzátor feltöltődését (és amely jól ismert a radioaktív bomlástörvényből is), megoldása:

\begin{matrix} [U_{C} (\infty) - U_{C} (t)] = [U_{C} (\infty) - U_{C} (0)] e^{- \frac{3 t}{2 τ}}, \end{matrix}

amiből látható, hogy a kondenzátor akkor töltődik fel a maximális érték felére, ha

\begin{matrix} e^{- \frac{3 t}{2 τ}} = \frac{1}{2}, azaz t = \frac{2}{3} τ ln 2 = 0, 0924 s . \end{matrix}

*

Az ünnepélyes eredményhirdetés és díjkiosztás a járványhelyzet miatt elmaradt. Helyette az eredetileg meghirdetett időpontban, 2020. november 20-án délután 3 órakor a verseny honlapjára került fel mindaz, ami az eredményhirdetésen elhangzott volna. Ismertetésre kerültek az 50 és 25 évvel ezelőtti Eötvös-verseny feladatai, és az akkori díjazottak egy részének visszaemlékezései: az 50 évvel ezelőttiek közül Horváth Péter és Tichy-Rács Ádám, a 25 évvel ezelőttiek közül Lovas Rezső, Tóth Gábor Zsolt és Varga Dezső küldött üzenetet.
Ezt követte a 2020. évi verseny feladatainak és megoldásainak bemutatása (az 1. feladat megoldását Tichy Géza, a 2. feladatét Vigh Máté, a 3. feladatét Vankó Péter írta le), majd az eredmények közlése:
Egyetlen versenyző sem oldotta meg mindhárom feladatot, így a versenybizottság nem adott ki első díjat.
Az első feladat helyes és a harmadik feladat lényegében helyes megoldásáért, valamint a második feladatban elért részeredményekért második díjat nyert Bonifert Balázs, a budapesti Baár-Madas Református Gimnázium 12. osztályos tanulója, Horváth Norbert tanítványa és Pácsonyi Péter, a BME mechatronikai mérnök alapszakos hallgatója, aki a Zalaegerszegi Zrínyi Miklós Gimnáziumban érettségizett Pálovics Róbert tanítványaként.
A második és a harmadik feladat kicsit hiányos megoldásáért harmadik díjat nyert Molnár Szabolcs, a BME fizika BSc szakos hallgatója, aki a Kecskeméti Katona József Gimnáziumban érettségizett Sáróné Jéga-Szabó Irén tanítványaként.
Az első feladat hibátlan megoldásáért dicséretet kapott Fekete Dezső Domonkos, a BME fizika BSc szakos hallgatója, aki a Kecskeméti Katona József Gimnáziumban érettségizett Sáróné Jéga-Szabó Irén tanítványaként, Selmi Bálint, a Pécsi Leőwey Klára Gimnázium 12. osztályos tanulója, Simon Péter, Kotek László és Pálfalvi László tanítványa, valamit Sepsi Csombor Márton, a Zalaegerszegi Zrínyi Miklós Gimnázium 12. osztályos tanulója, Kovács Tibor tanítványa.
A második díjjal Zimányi Gergely adományából 75 ezer, a harmadik díjjal 55 ezer, a dicsérettel 35 ezer forint pénzjutalom jár. A díjazottak tanárai az Eötvös Loránd emlékalbumot kapják. Az Eötvös Loránd Fizikai Társulatot a Nanorobot Vagyonkezelő Kft. és az Andersen Adótanácsadó Zrt. támogatja. Köszönjük az adományozók önzetlen támogatását!

\begin{matrix} Tichy Géza, Vankó Péter, Vigh Máté \end{matrix}

^{$^{*}$}Részletek a verseny honlapján: http://eik.bme.hu/~vanko/fizika/eotvos.htm.