Cím: Kacifántos kerítés - I. rész
Szerző(k):  Schmieder László 
Füzet: 2020/november, 481 - 485. oldal  PDF  |  MathML 
Témakör(ök): Számítástechnika, informatika, Szakmai cikkek, Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ezen a néven jelent meg a CEOI (Közép-Európai Informatikai Diákolimpia) idei első feladata. A teljes szöveg elérhető a következő címen:


 
1. feladat: Olvassuk el és értelmezzük a problémát, készítsünk néhány példát, rajzoljunk, majd próbáljuk meg egy-két mondatban összefoglalni, hogy pontosan mit kérdez a feladat.
 

A feladat téglalapok megszámolását kéri. Kombinatorikai feladatok között láthattunk már hasonlót: számoljuk meg, hogy az A(ax,ay) és B(bx,by) pontok mint szemközti csúcsok által meghatározott, a koordinátatengelyekkel párhuzamos oldalú téglalapban hány olyan téglalap van, amelynek csúcsai egész koordinátákkal rendelkeznek és oldalai szintén a koordinátatengelyekkel párhuzamosak.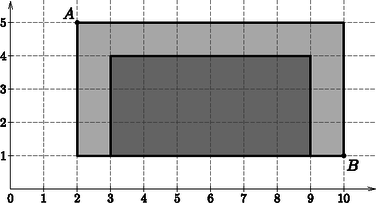
 
2. feladat: Adjunk módszert a téglalapok megszámolására egy a×b oldalú téglalap esetén.
 
 

Válasszunk a téglalap kerületén vagy belsejében tetszőlegesen két egész koordinátájú pontot. Ha a választott pontok egyenese nem párhuzamos egyik tengellyel sem, akkor meghatároznak egy téglalapot úgy, hogy ezt a két pontot tekintjük két szemközti csúcsnak. Így az első csúcs elhelyezésére (a+1)⋅(b+1) lehetőség adódik, míg a másodikra a⋅b. Ezen a módon minden téglalapot négyszer számoltunk: kiválasztottuk a bal felső-jobb alsó csúcspárt kétszer, és a bal alsó-jobb felső csúcspárt is kétszer. Ezért a téglalapok száma
(a+1)⋅(b+1)⋅a⋅b4.

A kacifántos kerítés téglalapokból épül föl, de a megszámolandó téglalapok átnyúlnak a kerítést alkotó téglalapokon, tehát a problémát még nem oldottuk meg. A továbbiakban vizsgáljuk a következő bemenethez tartozó kerítést. Az első sorban a kerítéselemek N száma, a másodikban azok hi magassága és a harmadik sorban az elemek wi szélessége található (1≤i≤N):
 
11   3 5 4 2 6 4 3 3 1 5 1   2 1 1 2 2 1 1 2 1 2 2   
 

Helyezzük el a kerítés bal alsó sarkát a koordináta-rendszer középpontjába. Nézzük, hogyan lehetne a téglalapoknak csúcsokat választani a kerítésen. Látjuk, hogy például a (3,2) és (11,1) pontok, mint (bal, felső) és (jobb, alsó) csúcsok meghatároznak egy megszámolandó téglalapot, miközben az egyik csúcs a második (vagy harmadik), míg a másik csúcs a nyolcadik kerítéselemen található.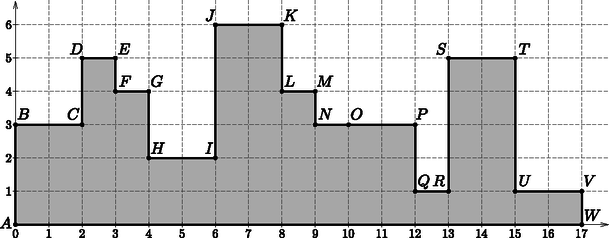
 
 

3. feladat: Találjunk ki egyszerű algoritmust, ami megszámolja a keresett téglalapokat.
 
Ha a kerítés méretei a példához hasonlóan kis számok, akkor nem is olyan nehéz algoritmust készíteni. Tekintsük a kerítés egész koordinátájú csúcsai közül azokat, amelyek lehetnek egy téglalap bal felső csúcsai, és válasszunk mindegyikhez megfelelő jobb alsó csúcsokat. Például a (3,3) ponthoz jobb alsó csúcsként kiválaszthatjuk a (4,2), (4,1), (4,0) pontokat. De az (1,2) ponthoz már sokkal több jobb alsó csúcs válaszható, a legtávolabbi a (12,0). Az előbbi kombinatorikus gondolatmenethez hasonlóan megszámolhatjuk minden bal felső csúcshoz a lehetséges jobb alsó csúcsokat. Az (1,2) pont esetén a jobb alsó csúcsok x koordinátája 2-től 12-ig, míg y koordinátája 0-tól 1-ig terjedhet. Így a meghatározott téglalapok száma 11⋅2=22.
A feladat tehát megoldható úgy, hogy minden lehetséges bal felső (b,f) csúcshoz meghatározzuk a tőle legtávolabbi olyan jobb alsó (j,a) csúcsot, amivel olyan téglalapot alkot, melynek minden pontja a kerítésen van. A bal felső csúcshoz rajzolható összes téglalap benne van ebben az előbbi, legnagyobb téglalapban. Az fenti kombinatorikai gondolatmenethez hasonlóan ezek száma (j-b+1)⋅(f-a+1). A jobb alsó csúcs mindig a kerítés alján van, tehát a=0, míg a jobb oldali utolsó megfelelő pont x koordinátáját úgy kapjuk, hogy elindulunk az X tengely pozitív irányában a (b,f) pontból, és az első olyan kerítést alkotó téglalapnál megállunk, amelynek magassága kisebb, mint f. Ha mind megfelelő, akkor a kerítés végéig megyünk.
Nézzük a megoldás algoritmusát. A bemenet beolvasásakor értéket adunk az N egész változónak, valamint a h[0..N-1] és w[0..N-1] egészeket tartalmazó N méretű tömbnek. Ezeket, valamit a továbbiakban használt tömböket 0-tól indexeljük. Ezt a műveletsort végzi el a Beolvas() eljárás, amit nem részletezünk.
Mivel a lehetséges bal felső csúcsoktól az X tengely pozitív irányában elindulva keresni fogunk, ezért tudnunk kell az egyes kerítést alkotó téglalapok abszolút helyzetét az X tengelyen. Ehhez hozzunk létre az el[0..N] tömböt, amelynek k-adik eleme megadja a k-adik kerítéselem bal oldalának x koordinátáját (0≤k<N), míg N-edik eleme az utolsó kerítéselem jobb oldalának helyét, azaz a kerítés végét. Természetesen úgy is nézhetjük, hogy az el[k+1] a k-adik kerítéselem jobb vége, vagyis jobb oldalának x koordinátája. A tömb értékeinek számítását a következő eljárás végzi:
 

Eljárás TeglalapokEleje(N,w[0..N-1],el[0..N])
 el[0] := 0
 Ciklus k := 0-tól N-1-ig
  el[k+1] := el[k]+w[k]
 Ciklus vége
Eljárás TeglalapokEleje vége

 
A továbbiakban megszámoljuk mindegyik kerítéselemnél azokat a téglalapokat, amelyek bal felső csúcsa a kerítéselemen, de nem annak jobb szélső oldalán található. Utóbbiakat a következő kerítéselemhez soroljuk. Mivel az utolsó kerítéselem jobb oldalán nem lehetnek bal felső csúcsok, így minden lehetséges bal felső csúcsot pontosan egyszer számolunk. A számítást a k-adik kerítéselemre a
KeritesElem() függvény végzi. Felülről lefelé haladunk, mivel a bal felső csúcsok h[k]-tól 1-ig helyezkedhetnek el. Minden felso szinthez (y értékhez) megnézzük, hogy meddig lehet jobbra elmenni a KeresJobb() függvény segítségével, majd a kerítéselem minden lehetséges bal értékétől kiszámoljuk a (bal,felso) koordinátákból kiinduló téglalapok számát.
 

Függvény KeritesElem(N,h[0..N-1],w[0..N-1],k,el[0..N]) : Egész
 darab := 0
 Ciklus felso := 1-től h[k]-ig
  meddig := KeresJobb(N,h,k,felso)
  jobb := el[meddig]
  Ciklus bal := el[k]-tól (el[k]+w[k]-1)-ig
   darab := darab + (jobb-bal)*(felso-0)
  Ciklus vége
 Ciklus vége
 KeritesElem := darab
Függvény KeritesElem vége

 
A KeresJobb() függvény megadja, hogy a k-adik kerítéselem felso magasságú pontjából meddig lehet jobbra menni úgy, hogy a kerítésen maradjunk. Minden m>k-adik kerítéselem megfelelő, amely nem alacsonyabb a felso magasságnál. Ha mindegyik megfelelő, akkor a kerítés jobb végénél állunk meg. A függvény visszaadja az első nem megfelelő kerítéselem indexét, illetve N-et, ha a kerítés végéig minden elem elég magas.
 

Függvény KeresJobb(N,h[0..N-1],k,felso) : Egész
 m := k+1
 Ciklus amíg m<N és h[m]≥felso
  m := m+1
 Ciklus vége
 KeresJobb := m
Függvény KeresJobb vége

 

A KacifantosKerites függvény adja a feladat megoldását: a beolvasás és az előkészítő műveletek után megszámolja az egyes kerítéselemekből bal felső csúcsokkal készíthető téglalapokat, és visszaadja azok 1000000007-tel vett osztási maradékát.
 

Függvény KacifantosKerites() : Egész
 Beolvasas(N,h,w)
 TeglalapokEleje(N,w,el)
 darab := 0
 Ciklus k := 0-tól N-1-ig
  darab := darab + KeritesElem(N,h,w,k,el)
 Ciklus vége
 KacinfatosKerates := darab MOD 1000000007
Függvény KacifantosKerites vége

 

Feltételezzük, hogy az algoritmusból készített programban az esetlegesen nagy számértékek elférnek a használt egész típusban és a műveletek nem okoznak túlcsordulást. A megoldás azonban a nagy számú és nagyságrendű bemenetekkel sajnos ettől függetlenül nem boldogul. A versenyen kevés pontot kapott volna, mivel a futásidő nagyobb h[] és N értékek esetén meghaladja az időkeretet. Ez érthető, hiszen a KeresJobb() függvény ∑i=0N-1hi alkalommal hívódik meg, vagyis az y=0 kivételével minden kerítéselem magasságnál, míg a benne szereplő ciklus átlagos lépésszáma a kerítéselemek N számával arányos. Tehát hatékonyabb algoritmusra lesz szükségünk, amiben nem szerepel a KeresJobb függvényhez hasonló keresés.
Az előző algoritmus kerítéselemeken választott bal felső csúcsokat, és a jobb alsó csúcsokat tőle jobbra, a többi kerítéselemet vizsgálva kereste. Ne ragaszkodjunk feltétlenül a kerítés pontjainak ilyen csoportosításához.
 
4. feladat: Próbáljuk olyan téglalapokra bontani a kerítést, ahol magától adódik egy-egy bal felső csúcshoz a legtávolabbi jobb alsó csúcs.
 

Vegyük észre, hogy ha egy kerítéselem mindkét szomszédjánál magasabb, akkor azok a csúcsai, amelyek mindkét szomszéd magasságánál nagyobb y koordinátával rendelkeznek, csak olyan csúcsokkal alkothatnak a kerítésen téglalapot, amelyek az adott kerítéselemen vannak. Például tekintsük a vizsgált bemenetnél a (6,4), (8,4), (8,6) és (6,6) csúcsok által meghatározott téglalapot. Az ezen fekvő bal felső csúcsokhoz ‐ kivéve az alsó oldalélt ‐ csak ezen a kerítéselemen lévő csúcsok közül választhatunk jobb alsót, tehát csak a 6≤x≤8 értékek jöhetnek számításba. Ez éppen az adott kerítéselem két vége, tehát ekkor semmilyen X tengely irányú keresésre nincs szükség.
Gondoljuk tovább a dolgot. Ha az előbbi kerítésrészre eső bal felső csúcsokkal alkotott téglalapokat megszámoltuk, akkor gyakorlatilag elhagyhatjuk ezt a részét a kerítésnek, hiszen jobb alsó csúcsként is megszámoltuk minden pontját. Amennyiben további, hasonlóan kiemelkedő részek vannak a kerítésen, akkor azokban is számolhatunk. Így a példában a (2,4) és a D, E, F pontok által alkotott vagy az RSTU téglalap esetében. Az alábbi ábrán satírozással jelöljük a szóban forgó kiemelkedéseket.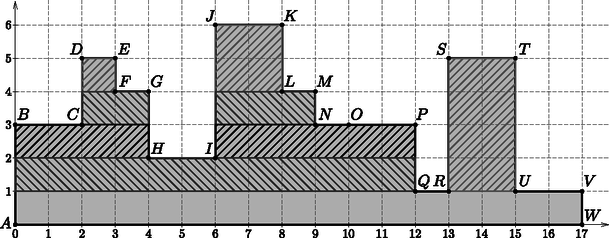
 
 

Ezeket a kerítésrészeket elhagyva ismét olyan kerítés keletkezik, amelynek vagy vannak kiemelkedései, vagy egyetlen téglalap az egész kerítés. Így a számolás folytatható pl. a (6,3), N, M, (6,4) téglalappal. Amennyiben lépésről-lépésre minden kiemelkedést a számolás után elhagyunk, akkor végül egy téglalap marad, amivel készen is vagyunk. A megoldáshoz tehát csak arra van szükség, hogy minél egyszerűbben meghatározzuk a kiemelkedéseket.
 
5. feladat: Gondolkozzunk olyan algoritmuson, ami az adatok alapján végigmegy a kiemelkedéseken és megszámolja azokat a téglalapokat, amelyek bal felső csúcsa ezeken található.
 

A cikk folytatásában választ adunk az 5. feladatra és hatékony algoritmust készítünk a versenyen kitűzött problémához. Természetesen a leírt gondolatmeneten kívül más ötlet alapján is lehet megoldást készíteni. Az utóbbi évek CEOI feladatai szerepelnek a http://mester.inf.elte.hu adatbázisában, így programunk helyességét és hatékonyságát ellenőrizhetjük a segítségével.