Cím:	Megoldásvázlatok a 2020/7. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Németh László, Fonyód
Füzet:	2020/november, 463 - 474. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Melyek azok az $x$, $y$ egész számok, amelyekre egyszerre teljesül, hogy: $a)$ $x^2+y^2\le 25;$ $b)$ $|x|+|y|\ge 5;$ $c)$ $\text{log}{}_2\left(y+1-x^2\right)\ge 0?$ (12 pont)   Megoldás. Az $a)$ feltételnek megfelelő valós számpárok halmaza a koordinátarendszerben egy origó középpontú, 5 egység sugarú zárt körlemezzel szemléltethető. $b)$ Itt a négy negyedben az alábbiak szerint alakulnak a halmazok:   ${\displaystyle \begin{array}{c}{\displaystyle \text{ ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo>≥</mo><mn>0</mn></math> és <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>≥</mo><mn>0</mn></math>, akkor <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>≥</mo><mo stretchy="false">-</mo><mi>x</mi><mo stretchy="false">+</mo><mn>5</mn></math>;}}\hfill \\ {\displaystyle \text{ ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo>≤</mo><mn>0</mn></math> és <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>≥</mo><mn>0</mn></math>, akkor <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>≥</mo><mi>x</mi><mo stretchy="false">+</mo><mn>5</mn></math>;}}\hfill \\ {\displaystyle \text{ ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo>≤</mo><mn>0</mn></math> és <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>≤</mo><mn>0</mn></math>, akkor <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>≤</mo><mo stretchy="false">-</mo><mi>x</mi><mo stretchy="false">-</mo><mn>5</mn></math>;}}\hfill \\ {\displaystyle \text{ ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo>≥</mo><mn>0</mn></math> és <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>≤</mo><mn>0</mn></math>, akkor <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>≤</mo><mi>x</mi><mo stretchy="false">-</mo><mn>5</mn></math>. }}\hfill \end{array}}$   $c)$ $\text{log}{}_2\left(y+1-x^2\right)\ge 0$, $\text{log}{}_2\left(y+1-x^2\right)\ge \text{log}{}_{2}1\Rightarrow$ (mivel a $\text{log}{}_{2}x$ függvény szigorúan monoton növő) $y+1-x^2\ge 1$, tehát $y\ge x^2$ (a normálparabola és belső pontjai). (Ekkor $y+1-x^2>0$, tehát a logaritmus értelmezett.) Ha mindezeket, továbbá azt is figyelembe vesszük, hogy egész számokat keresünk, akkor a vonalkázott tartományban, illetve a határán levő rácspontok koordinátáit kapjuk.     A megoldások:   ${\displaystyle \begin{array}{ccc}{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mo stretchy="false">-</mo><mn>2</mn><mi>;</mi><mn>4</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mn>2</mn></math>; }}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>4</mn></math>;}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mo stretchy="false">-</mo><mn>1</mn><mi>;</mi><mn>4</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mn>1</mn></math>; }}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>4</mn></math>;}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>0</mn><mi>;</mi><mn>5</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>0</mn></math>; }}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>5</mn></math>;}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>1</mn><mi>;</mi><mn>4</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>4</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>1</mn></math>; }}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>4</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>4</mn></math>;}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>2</mn><mi>;</mi><mn>4</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>5</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>2</mn></math>; }}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>5</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>4</mn></math>. }}\hfill \end{array}}$   2. $a)$ Az egyszerű hétpontú gráf csúcsainak foka rendre $\mathrm{3,2,4,1,2};$ a másik kettőt nem ismerjük. Állapítsuk meg ezeket, ha a gráfnak $11$ éle van, valamint a gráf megrajzolható egy folytonos vonallal úgy, hogy mindegyik élén pontosan egyszer haladtunk át. $b)$ Adjunk meg három különböző irracionális számot úgy, hogy a három szám összege és bármelyik kettő szorzata is racionális szám legyen. $c)$ Mutassuk meg, hogy az $A$ és $B$ kijelentések tetszőleges logikai értékére igaz a $\neg \left(A\to B\right)=A^\neg B$ egyenlőség. (12 pont)   Megoldás. $a)$ Az egyszerű gráf csúcsai fokainak összege az élek számának kétszerese, ezért az ismeretlen fokszámok összege 10. A hétpontú gráf csúcsának foka legfeljebb 6 lehet, így a két fokszám 5, 5 vagy 4, 6. Az utolsó feltétel miatt a megoldás 4, 6, mert a másik esetben négy páratlan foka volna a gráfnak, ekkor azonban nem lenne nyitott Euler-vonala. Mivel ekkor van 6-odfokú csúcs, így a gráf összefüggő is, és ezért van nyitott Euler-vonala. $b)$ Pl.: $i_1=\sqrt[]{2}$,$i_2=2\sqrt[]{2}$, $i_3=-3\sqrt[]{2}$. A számok irracionálisak és különbözőek. $\begin{array}{c}{\displaystyle i_1+i_2+i_3=0;i_1\cdot i_2=4;i_1\cdot i_3=-6;i_2\cdot i_3=-12.}\end{array}$ $c)$ I. megoldás. Készítsük el az igazságtáblázatot:   ${\displaystyle \begin{array}{|ccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo stretchy="true">→</mo><mi>B</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>¬</mo><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>A</mi><mo stretchy="true">→</mo><mi>B</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mo>^</mo><mo>¬</mo><mi>B</mi></math> }}\hfill \\ \hfill {\displaystyle \text{i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h }}\hfill \\ \hfill {\displaystyle \text{i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i }}\hfill \\ \hfill {\displaystyle \text{h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h }}\hfill \\ \hfill {\displaystyle \text{h}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ i}}\hfill & \hfill {\displaystyle \text{ h}}\hfill & \hfill {\displaystyle \text{ h }}\hfill \\ \hline\end{array}}$   Az utolsó két oszlopban rendre ugyanazok a logikai értékek vannak, tehát a két kifejezés egyenlő. II. megoldás. Ismert az $A\to B=\neg A\vee B$ azonosság. $\neg \left(A\to B\right)=\neg \left(\neg A\vee B\right)$, most alkalmazzuk a De-Morgan azonosságot: $\neg \left(\neg A\vee B\right)=\neg \neg A^\neg B=A^\neg B$.   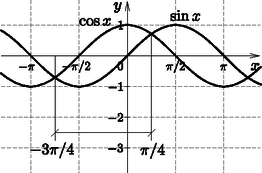3. Oldjuk meg a valós számok halmazán a $\begin{array}{c}{\displaystyle \text{sin}x+\text{cos}x=\frac{1-\text{sin}\left(2x\right)}{\text{cos}\left(2x\right)}}\end{array}$ egyenletet. (13 pont)   Megoldás. Kikötés: $\text{cos}\left(2x\right)\ne 0$; alakítsuk az egyenlet jobb oldalát: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{sin}x+\text{cos}x}& {\displaystyle =\frac{\text{sin}{}^{2}x+\text{cos}{}^{2}x-2\text{sin}x\text{cos}x}{\text{cos}{}^{2}x-\text{sin}{}^{2}x}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{{\left(\text{cos}x-\text{sin}x\right)}^2}{\left(\text{cos}x-\text{sin}x\right)\left(\text{cos}x+\text{sin}x\right)}=\frac{\text{cos}x-\text{sin}x}{\text{cos}x+\text{sin}x};}\hfill \\ \hfill {\displaystyle {\left(\text{sin}x+\text{cos}x\right)}^2}& {\displaystyle =\text{cos}x-\text{sin}x\mathrm{,}}\hfill \end{array}}$ (itt egy újabb feltétel adódott: $\text{cos}x\ge \text{sin}x$), $\begin{array}{c}{\displaystyle \text{sin}{}^{2}x+2\text{sin}x\text{cos}x+\text{cos}{}^{2}x=\text{cos}x-\text{sin}x\mathrm{,}1+\text{sin}\left(2x\right)=\text{cos}x-\text{sin}x\mathrm{.}}\end{array}$ Emeljünk négyzetre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 1+2\text{sin}\left(2x\right)+\text{sin}{}^2\left(2x\right)}& {\displaystyle =1-\text{sin}\left(2x\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{sin}{}^2\left(2x\right)+3\text{sin}\left(2x\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \text{sin}\left(2x\right)\left[\text{sin}\left(2x\right)+3\right]}& {\displaystyle =\mathrm{0,}}\hfill \end{array}}$ ahonnan $\text{sin}\left(2x\right)=0$, vagy $\text{sin}\left(2x\right)+3=0$. Ez utóbbi lehetetlen, így $2x=k\pi$, $x=\frac{k\pi }{2}$, $k\in \text{Z}$. A $\text{cos}(2\cdot \frac{k\pi }{2})\ne 0$ feltételnek megfelelnek a gyökök, mert a bal oldal értéke 1, vagy $-1$, attól függően, hogy $k$ páros, vagy páratlan. A $\text{cos}x\ge \text{sin}x$ egyenlőtlenség megoldását a függvények grafikonjainak ismeretében leolvassuk:     Ezt figyelembe véve a megoldások: $x_1=-\frac{\pi }{2}+2k\pi$; $x_2=2l\pi$, $k\mathrm{,}l\in \text{Z}$. (Ellenőrzéssel is meggyőződhetünk eredményeink helyességéről: az első gyökre $-1=-1$, a másodikra $1=1$ adódik, míg a $\frac{\pi }{2}+2k\pi$-re, illetve a $\left(2l+1\right)\pi$-re $1=-1$-et kapunk, ezek tehát nem gyökök.)   4. Két horgászegyesület, az Aligai Pecások és a Bélatelepi Horgászok közös edzőtáborozást tartottak $47$ fő részvételével. A csapatokban felnőtt és junior korosztályú csoportok voltak. Tudjuk, hogy: $a)$ minden csoport létszáma prímszám; $b)$ legkevesebben a junior Bélatelepi Horgászok, legtöbben a felnőtt Aligai Pecások vannak a táborban; $c)$ a felnőtt versenyzők összlétszáma osztható tízzel; $d)$ a két csapat felnőtt tagjainak létszáma között $10$-nél kisebb a különbség. Hányan vannak az egyes csoportokban? (14 pont)   Megoldás. Vezessük be a következő jelöléseket: felnőttek $A$, $B$; juniorok $a$, $b$ a csapatok kezdőbetűinek megfelelően. Így felírhatjuk az $A+a+B+b=47$ egyenletet, ahol az ismeretlenek pozitív prímek. Azonnal láthatjuk, hogy az egyik a 2, hiszen különben az összegnek párosnak kellene lennie. A $b)$ feltétel alapján ez a $b$, vagyis két junior Bélatelepi Horgász van a táborban. Ezután $A+a+B=45$, $a=45-\left(A+B\right)$. A $c)$ feltétel szerint $A+B$ osztható 10-zel, így a jobb oldal osztható 5-tel, mivel prím, $a=5$. $A+B=40$ (itt példát láthatunk a Goldbach-sejtésre, mely szerint minden 2-nél nagyobb páros szám felírható két prímszám összegeként). Több lehetőség is van, ezek: $3+37=11+29=17+23=40$. A $b)$ és $d)$ feltételeket figyelembe véve a megoldás: $A=23$; $B=17$; $a=5$; $b=2$. Az edzőtáborban 23 felnőtt és 5 junior Aligai Pecás, 17 felnőtt és 2 junior Bélatelepi Horgász van.   II. 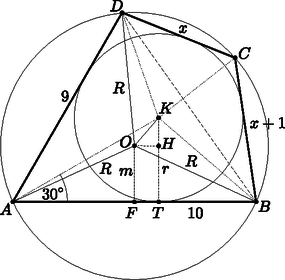rész     5. Egy húrnégyszög egyúttal érintőnégyszög is (bicentrikus négyszög). Két szomszédos oldala $9$, $10$ egység, az általuk bezárt szög ${60}^{\circ }$. Jelöljük $O$-val a körülírt, $K$-val a beírt kör középpontját. $a)$ Adjuk meg a másik két oldal hosszát. $b)$ Határozzuk meg a beírt- és a köréírt kör sugarát. $c)$ Milyen hosszú a $KO$ távolság? (16 pont)     Megoldás. $a)$ Az ábra jelöléseivel az érintőnégyszögre vonatkozó tétel szerint $AB+CD=DA+BC$.     Legyen $CD=x$, ekkor $BC=x+1$. Ha a $DAB\sphericalangle ={60}^{\circ }$, akkor a húrnégyszögekre igaz tétel miatt $BCD\sphericalangle ={120}^{\circ }$. Írjuk fel a koszinusz-tételt az $ABD▵$ $BD$ oldalára: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle B{D}^2}& {\displaystyle =9^2+{10}^2-2\cdot 9\cdot 10\cdot \frac{1}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle B{D}^2}& {\displaystyle =\mathrm{91,}BD=\sqrt[]{91};}\hfill \end{array}}$ majd írjuk fel a $BCD▵$-ben is a $BD$ oldalra: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 91}& {\displaystyle =x^2+{\left(x+1\right)}^2-2x\cdot \left(x+1\right)\cdot \left(-\frac{1}{2}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 91}& {\displaystyle =x^2+x^2+2x+1+x^2+x\mathrm{,}}\hfill \\ \hfill {\displaystyle 90}& {\displaystyle =3x^2+3x\Rightarrow 0=x^2+x-30;}\hfill \\ \hfill {\displaystyle x_{\mathrm{1,2}}}& {\displaystyle =\frac{-1\pm \sqrt[]{121}}{2}\Rightarrow x=5;CD=\mathrm{5,}BC=6.}\hfill \end{array}}$ $b)$ Az $ABD▵$ körülírt körének ‐ ami egyúttal a négyszögnek is körülírt köre ‐ sugara az ismert tétel szerint: $\begin{array}{c}{\displaystyle R=\frac{BD}{2\text{sin}{60}^{\circ }}=\frac{\sqrt[]{91}}{2\frac{\sqrt[]{3}}{2}}=\sqrt[]{\frac{91}{3}}\mathrm{.}}\end{array}$ A négyszög területe: $\begin{array}{c}{\displaystyle T=\frac{9\cdot 10\cdot \text{sin}{60}^{\circ }}{2}+\frac{5\cdot 6\cdot \text{sin}{120}^{\circ }}{2}=30\sqrt[]{3}\mathrm{.}}\end{array}$ Használhatjuk Brahmagupta képletét is: $T=\sqrt[]{\left(s-a\right)\left(s-b\right)\left(s-c\right)\left(s-d\right)}$, ahol $s=\frac{a+b+c+d}{2}=15$, tehát $T=\sqrt[]{5\cdot 6\cdot 9\cdot 10}=\sqrt[]{2700}=30\sqrt[]{3}$, vagy pedig a bicentrikus négyszögek területképletét: $T=\sqrt[]{abcd}$. A beírt kör sugarát legegyszerűbben az érintősokszögekre érvényes $sr=T$ összefüggés alkalmazásával kaphatjuk meg: $15r=30\sqrt[]{3}\Rightarrow r=2\sqrt[]{3}$. $c)$ I. megoldás. Az $ATK$ derékszögű háromszögben $\text{ctg}{30}^{\circ }=\frac{AT}{r}\Rightarrow AT=6$ $\Rightarrow OH=FT=AT-AF=1$. Írjuk fel a Pitagorasz-tételt az $AFO$ derékszögű háromszögben: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 5^2+m^2=R^2\Rightarrow m^2=\frac{91}{3}-25=\frac{16}{3};m=\frac{4}{\sqrt[]{3}}=\frac{4\sqrt[]{3}}{3};}\hfill \\ \hfill {\displaystyle HK=r-m=2\sqrt[]{3}-\frac{4\sqrt[]{3}}{3}=\frac{2\sqrt[]{3}}{3}\mathrm{.}}\hfill \end{array}}$ Végül ${OK}^2={OH}^2+{HK}^2$; ${OK}^2=1^2+(\frac{2\sqrt[]{3}}{3}{)}^2$; $OK=\frac{\sqrt[]{21}}{3}$. II. megoldás. Ha már kiszámítottuk a sugarakat, és ismerjük a bicentrikus négyszögek köreinek sugaraira, és e körök középpontjainak távolságára vonatkozó összefüggést, akkor a távolságot innen is megkaphatjuk. Az összefüggés: $\begin{array}{c}{\displaystyle \frac{1}{{\left(R-d\right)}^2}+\frac{1}{{\left(R+d\right)}^2}=\frac{1}{r^2}\mathrm{,}}\end{array}$ ahol $R$ a körülírt kör, $r$ a beírt kör sugara, $d$ a középpontok távolsága. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{{\left(R+d\right)}^2+{\left(R-d\right)}^2}{{\left(R-d\right)}^2{\left(R+d\right)}^2}}& {\displaystyle =\frac{1}{r^2};}\hfill \\ \hfill {\displaystyle \frac{R^2+2Rd+d^2+R^2-2Rd+d^2}{{\left(R^2-d^2\right)}^2}}& {\displaystyle =\frac{1}{r^2};2r^2\left(R^2+d^2\right)={\left(R^2-d^2\right)}^2\mathrm{.}}\hfill \end{array}}$ Helyettesítsük be a sugarakat: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2{\left(2\sqrt[]{3}\right)}^2\left(\frac{91}{3}+d^2\right)}& {\displaystyle ={\left(\frac{91}{3}-d^2\right)}^2;}\hfill \\ \hfill {\displaystyle 24\left(\frac{91}{3}+d^2\right)}& {\displaystyle =\frac{8281}{9}-\frac{182}{3}{d}^2+d^4;}\hfill \\ \hfill {\displaystyle 728+24d^2}& {\displaystyle =\frac{8281}{9}-\frac{182}{3}{d}^2+d^4/\cdot 9}\hfill \\ \hfill {\displaystyle 6552+216d^2}& {\displaystyle =8281-546d^2+9d^4;}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =9d^4-762d^2+\mathrm{1729,}}\hfill \\ \hfill {\displaystyle {\left(d^2\right)}_{\mathrm{1,2}}}& {\displaystyle =\frac{762\pm \sqrt[]{{762}^2-36\cdot 1729}}{18}=\frac{762\pm 720}{18}\mathrm{,}}\hfill \end{array}}$ $d_1^2=\frac{1482}{18}=\frac{247}{3}\Rightarrow d_1=\sqrt[]{\frac{247}{3}}\approx 9\mathrm{,}07$, ez azonban nem jó, mert $d<R$. $d_2^2=\frac{42}{18}=\frac{7}{3}\Rightarrow d=\sqrt[]{\frac{7}{3}}=\frac{\sqrt[]{21}}{3}$, ami egyezik az első megoldás eredményével.   Megjegyzés: Brahmagupta tételének levezetését több helyen, pl. Dr. Gerőcs László: Azok a csodálatos húrnégyszögek című könyvében is megtalálhatjuk. A bicentrikus négyszögekre vonatkozó tétel bizonyítását pl. Nemecskó István: Bicentrikus négyszögek (matematika.elte.hu/wp-content/uploads/2017/03/NemecskoIstvan.pdf) címen érhetjük el.   6. $a)$ Vizsgáljuk meg az $a_n=n^3-n^2$ sorozatot monotonitás és korlátosság szempontjából. Állításainkat igazoljuk. $b)$ Mutassuk meg, hogy a sorozat első $n$ tagjának összege $\begin{array}{c}{\displaystyle \frac{n\left(n+1\right)\left(n-1\right)\left(3n+2\right)}{12}\mathrm{.}}\end{array}$ (16 pont)   Megoldás. $a)$ A sorozat első néhány tagját kiszámolva $\mathrm{0,}\mathrm{4,}\mathrm{18,}\mathrm{48,}\mathrm{100,}\text{...}$ adódik, amiből a szigorúan monoton növekedés látszik. Igazolnunk kell, hogy $a_n<a_{n+1}$ minden $n\in {\text{Z}}^{+}$ esetén, tehát $\begin{array}{c}{\displaystyle n^3-n^2<{\left(n+1\right)}^3-{\left(n+1\right)}^2;n^3-n^2<n^3+3n^2+3n+1-n^2-2n-1;}\end{array}$ rendezve: $0<3n^2+n$, ami minden pozitív egészre fennáll. Idáig ekvivalens lépéseken át jutottunk, ezért a kiinduló állítás is igaz. A sorozat alulról korlátos, negatív tagja nincs, így tetszőleges negatív szám jó alsó korlátnak, felülről nem korlátos, azaz bármely pozitív $K$-hoz található $n_0$ küszöbindex, hogy minden $n>n_0$ esetén $a_n>K$ teljesül. (A küszöbindex nem lesz ,,éles'', ehhez egy harmadfokú egyenletet kellene megoldani.) Tekintsük a $b_n=\frac{n^3}{2}$ sorozatot. Az $a_n>b_n$; $n^3-n^2>\frac{n^3}{2}$; $\frac{n^3}{2}-n^2>0$; $\frac{n^2}{2}\left(n-2\right)>0$, minden $n>2$-re teljesül. Oldjuk meg a $b_n>K$ egyenlőtlenséget: $\frac{n^3}{2}>K$; $n>\sqrt[3]{2K}$. Mivel $a_n>b_n$, ezért bármely nagy pozitív $K$-hoz küszöbindexnek választhatjuk a $\sqrt[3]{2K}$ egészrészét. Beláttuk tehát, hogy az $a_n$ sorozat felülről nem korlátos. (Jelölhetjük ezt úgy is, hogy $\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}{a}_n=+\infty$.) $b)$ I. megoldás teljes indukcióval. $n=1$-re igaz, tegyük fel, hogy az állítás igaz $n$-re, azaz $\begin{array}{c}{\displaystyle \sum _{i=1}^n\left(i^3-i^2\right)=\frac{n\left(n-1\right)\left(n+1\right)\left(3n+2\right)}{12}\mathrm{.}}\end{array}$ Bizonyítjuk, hogy fennáll $n+1$-re is, vagyis ${\displaystyle \begin{array}{cc}\hfill {\displaystyle S_n+a_{n+1}}& {\displaystyle =S_{n+1}\mathrm{.}}\hfill \\ \hfill {\displaystyle \frac{n\left(n-1\right)\left(n+1\right)\left(3n+2\right)}{12}+{\left(n+1\right)}^3-{\left(n+1\right)}^2}& {\displaystyle =}\hfill \\ \hfill {\displaystyle =\frac{\left(n+1\right)\left[\left(n+1\right)-1\right]\left[\left(n+1\right)+1\right]\left[3\left(n+1\right)+2\right]}{12}\mathrm{,}}& {\displaystyle /:\left(n+1\right);\cdot 12}\hfill \\ \hfill {\displaystyle n\left(n-1\right)\left(3n+2\right)+12{\left(n+1\right)}^2-12\left(n+1\right)}& {\displaystyle =n\left(n+2\right)\left(3n+5\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(n^2-n\right)\left(3n+2\right)+12n^2+24n+12-12n-12}& {\displaystyle =\left(n^2+2n\right)\left(3n+5\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 3n^3-3n^2+2n^2-2n+12n^2+12n}& {\displaystyle =3n^3+6n^2+5n^2+10n\mathrm{,}}\hfill \\ \hfill {\displaystyle 3n^3+11n^2+10n}& {\displaystyle =3n^3+11n^2+10n\mathrm{,}}\hfill \end{array}}$ ekvivalens lépéseken keresztül azonosságot kaptunk, tehát a kiinduló egyenlőség is igaz, ezzel a képlet helyességét igazoltuk. II. megoldás. Ismert, hogy $\sum _{i=1}^n{i}^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$; illetve $\sum _{i=1}^n{i}^3=[\frac{n\left(n+1\right)}{2}{]}^2$. Ezeket felhasználva ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\sum }_{i=1}^n}& {\displaystyle \left(i^3-i^2\right)={\left[\frac{n\left(n+1\right)}{2}\right]}^2-\frac{n\left(n+1\right)\left(2n+1\right)}{6}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{n\left(n+1\right)}{2}\left[\frac{n\left(n+1\right)}{2}-\frac{2n+1}{3}\right]=\frac{n\left(n+1\right)}{2}\cdot \frac{3n\left(n+1\right)-2\left(2n+1\right)}{6}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{n\left(n+1\right)}{2}\cdot \frac{3n^2+3n-4n-2}{6}=\frac{n\left(n+1\right)}{2}\cdot \frac{3n^2-n-2}{6}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{n\left(n+1\right)}{2}\cdot \frac{\left(n-1\right)\left(3n+2\right)}{6}=\frac{n\left(n-1\right)\left(n+1\right)\left(3n+2\right)}{12}\mathrm{.}}\hfill \end{array}}$   7. Anna és Bálint szabályos dobókockával játszik. Felváltva dobnak, ha a dobott szám prímszám, akkor a számegyenesen álló bábuval egyet jobbra, ha összetett szám, akkor egyet balra lépnek. Ha egyik sem, akkor a bábu helyben marad. A bábu kezdetben a nullán áll, összesen hatszor fognak dobni. Előtte fogadnak arra, hogy a játék végén melyik számon áll majd a bábu. Anna az egyesre, Bálint a kettesre fogad. $a)$ Kinek mekkora esélye van a nyerésre? Tegyük fel, hogy Anna nyerte a fogadást. $b)$ Mennyi a valószínűsége, hogy a játék során egyszer dobtak egyest? (16 pont)   Megoldás. $a)$ Prímszámok: 2, 3, 5; összetett számok: 4, 6; egyik sem: 1. Annak esélye, hogy a bábu egy dobás után jobbra lép $\frac{3}{6}=\frac{1}{2}$, jelöljük ezt $p_{\text{jobbra}}$-val. Hasonlóképpen: $p_{\text{balra}}=\frac{2}{6}=\frac{1}{3}$, $p_{\text{helyben}}=\frac{1}{6}$. Számítsuk ki Anna nyerési esélyét. Ahhoz, hogy 6 dobás után a bábu az 1-esen álljon, az alábbiak szerint léphetett (tetszőleges sorrendben): $\begin{array}{c}{\displaystyle \text{jhhhhh; ennek valószínűsége:}6\cdot {\left(\frac{1}{2}\right)}^1\cdot {\left(\frac{1}{3}\right)}^0\cdot {\left(\frac{1}{6}\right)}^5=\frac{1}{2592}\mathrm{,}}\end{array}$ vagy $\begin{array}{c}{\displaystyle \text{jjbhhh; ennek valószínűsége:}\frac{6!}{2!\cdot 3!}\cdot {\left(\frac{1}{2}\right)}^2\cdot {\left(\frac{1}{3}\right)}^1\cdot {\left(\frac{1}{6}\right)}^3=\frac{60}{2592}\mathrm{,}}\end{array}$ vagy $\begin{array}{c}{\displaystyle \text{jjjbbh; ennek valószínűsége:}\frac{6!}{3!\cdot 2!}\cdot {\left(\frac{1}{2}\right)}^3\cdot {\left(\frac{1}{3}\right)}^2\cdot {\left(\frac{1}{6}\right)}^1=\frac{360}{2592}\mathrm{.}}\end{array}$ Anna nyerési esélye ezek összege: $P\left(\text{Anna nyert}\right)=\frac{421}{2592}\approx 0\mathrm{,}1624$. Hat dobás után a 2-esre a következőképpen kerülhetett a bábu (a lépések sorrendje tetszőleges): $\begin{array}{c}{\displaystyle \text{jjhhhh; ennek valószínűsége:}\frac{6!}{2!\cdot 4!}\cdot {\left(\frac{1}{2}\right)}^2\cdot {\left(\frac{1}{3}\right)}^0\cdot {\left(\frac{1}{6}\right)}^4=\frac{5}{1728}\mathrm{,}}\end{array}$ vagy $\begin{array}{c}{\displaystyle \text{jjjbhh; ennek valószínűsége:}\frac{6!}{3!\cdot 2!}\cdot {\left(\frac{1}{2}\right)}^3\cdot {\left(\frac{1}{3}\right)}^1\cdot {\left(\frac{1}{6}\right)}^2=\frac{120}{1728}\mathrm{,}}\end{array}$ vagy ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{jjjjbb; ennek valószínűsége:}\frac{6!}{4!\cdot 2!}\cdot {\left(\frac{1}{2}\right)}^4\cdot {\left(\frac{1}{3}\right)}^2\cdot {\left(\frac{1}{6}\right)}^0=\frac{180}{1728}\mathrm{,}}\hfill \\ \hfill {\displaystyle P\left(\text{Bálint nyert}\right)=\frac{5}{1728}+\frac{120}{1728}+\frac{180}{1728}=\frac{305}{1728}=\approx 0\mathrm{,}1765.}\hfill \end{array}}$ $b)$ Jelölje $A$ azt az eseményt, hogy Anna nyert; $C$, hogy egyszer dobtak egyest. $\begin{array}{c}{\displaystyle P\left(AC\right)=\frac{360}{2592};P\left(A\right)=\frac{421}{2592}\mathrm{,}P\left(C\mid A\right)=\frac{P\left(AC\right)}{P\left(A\right)}=\frac{\frac{360}{2592}}{\frac{421}{2592}}=\frac{360}{421}\approx 0\mathrm{,}8551.}\end{array}$   8. A $2$ egység élű kocka egyik csúcsát jelöljük $A$-val, majd állítsunk egyenlő hosszú szakaszokat a kocka $A$-val érintkező lapjainak középpontjába, az adott lapokra merőlegesen kifelé. A szakaszok lapra nem illeszkedő végpontjait jelöljük $P$, $Q$, $R$-rel. $a)$ Milyen hosszúak a szakaszok, ha az $A$, $P$, $Q$, $R$ pontok egy síkban vannak? A $2$ egység élű kocka lapjaira kifelé egyenlő magasságú, $2$ egység oldalú négyzet alapú egyenes gúlákat helyezünk úgy, hogy a gúla alapja egybeesik a kocka adott lapjával. $b)$ Mekkora a gúla magassága, ha az így kapott testnek van körülírt és beírt gömbje? $c)$ Mekkora a gúla magassága abban az esetben, ha az így keletkezett poliédernek $14$ csúcsa, $12$ lapja és $24$ éle lett? (16 pont)   Megoldás. $a)$ I. megoldás. A kocka középpontja $O$, a felső lapközéppont $K$. Az $OKA\sphericalangle ={90}^{\circ }$, $AOK\sphericalangle =\phi$.     1. ábra   A kocka $A$-val érintkező lapjainak középpontjai által meghatározott sík merőleges az $A$-ból induló testátlóra. Ez ugyanaz a sík, mint amit az $A$-ból induló élek másik végén levő csúcsok határoznak meg, ezek pedig $A$-val együtt egy szabályos háromszög alapú, egyenlő oldalélű tetraédert alkotnak, amelynek az alaphoz tartozó magasság egyenese $AO$. Akkor lesz a négy pont egy síkban, ha $PAO\sphericalangle ={90}^{\circ }$ (és $QAO\sphericalangle =RAO\sphericalangle ={90}^{\circ }$). Ekkor az $AOK▵\cong POA▵$, mert két szögük ($\phi$, ${90}^{\circ }$) egyenlő, $\Rightarrow \frac{1}{\sqrt[]{3}}=\frac{\sqrt[]{3}}{1+x}$, $1+x=3\Rightarrow x=2$. Az $A$, $P$, $Q$, $R$ pontok akkor lesznek egy síkban, ha a merőleges szakaszok hossza 2 egység.     2. ábra   II. megoldás. A $QOP$ háromszögben $O$-nál derékszög van, a $QO$ befogó és $OP$ befogó $1+x$, ezért a $QP$ átfogó $\sqrt[]{2}\left(1+x\right)$ ($QR$, $RP$ hasonlóképpen), $AP=AQ=AR=\sqrt[]{2+x^2}$ ($AKP$ derékszögű háromszög befogói $\sqrt[]{2}$ és $x$, átfogó $AP$, a másik kettő ugyanígy). Ha a négy pont egy síkban van, akkor a $PQR$ szabályos háromszög körülírt körének középpontja $A$ (mert egyenlő távol van a csúcsoktól), ezért a $PAR\sphericalangle ={120}^{\circ }$. Innen kétféleképpen is befejezhetjük: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{sin}{60}^{\circ }=\frac{\frac{\sqrt[]{2}\left(1+x\right)}{2}}{\sqrt[]{2+x^2}};\frac{\sqrt[]{3}}{2}\sqrt[]{2+x^2}=\frac{\sqrt[]{2}\left(1+x\right)}{2};}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle 3\left(2+x^2\right)=2{\left(1+x\right)}^2;}\hfill \\ \hfill {\displaystyle 6+3x^2=2+4x+2x^2;x^2-4x+4=0;}\hfill \\ \hfill {\displaystyle {\left(x-2\right)}^2=0\Rightarrow x=2.}\hfill \end{array}}$ 2. 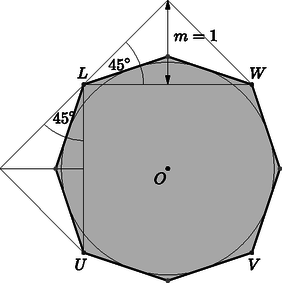Írjuk fel a koszinusz-tételt $RP$-re: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left[\sqrt[]{2}\left(1+x\right)\right]}^2=}\hfill \\ \hfill {\displaystyle =2+x^2+2+x^2-2\left(2+x^2\right)\left(-\frac{1}{2}\right);}\hfill \\ \hfill {\displaystyle 2\left(1+2x+x^2\right)=3x^2+6\Rightarrow x=2.}\hfill \end{array}}$ $b)$ A kocka körülírt gömbjének sugara $\sqrt[]{3}$. Ha a gúlák ötödik (a kocka csúcsaitól különböző) csúcsa is ezen a gömbön van, akkor magasságuk $m=\sqrt[]{3}-1$. Ebben az esetben beírt gömbje is van a testnek, mint az a metszeten látható, mert a magasság kisebb 1-nél. (Akkor nincs beírt gömb, ha a gúlák magassága nagyobb 1-nél, ugyanis ekkor $L$-nél, $U\mathrm{,}V\mathrm{,}W$-nél konkáv szög keletkezik.)     3. ábra     4. ábra   A megoldás tehát: $m=\sqrt[]{3}-1$.   $c)$ A 3. ábra szerinti testeknek ,,általában'' 24 lapjuk (14 csúcsuk és 36 élük) van. Ahhoz, hogy a lapok száma felére változzon, az kell, hogy két olyan háromszög, melyek egy eredeti kocka élben közös oldallal rendelkeztek, egy síkba kerüljenek, azaz a poliédernek egy lapját alkossák. Ez akkor következik be, ha a gúlák magassága 1 egység, ugyanis ebben az esetben az oldallapok az alaplappal ${45}^{\circ }$-os szöget zárnak be. Most az élek száma 12-vel csökken, hiszen eltűnnek a kocka élei, így az élek száma 24 lesz, a csúcsok száma nem változik. Az $m=1$ magasságú gúlák tehát olyan poliédert eredményeznek, melyeknek 14 csúcsuk, 12 lapjuk és 24 élük van (5. ábra), más magasság esetén a lapok, élek száma ettől különböző. A megoldás: $m=1$.     5. ábra   Megjegyzés. A kapott poliéder jó példa arra, attól, hogy egy testet egybevágó síkidomok határolnak, nem biztos, hogy szabályos test az illető. Ezt a testet ugyanis egybevágó rombuszok határolják, de különböző térszögleteik miatt mégsem szabályos a test.   9. 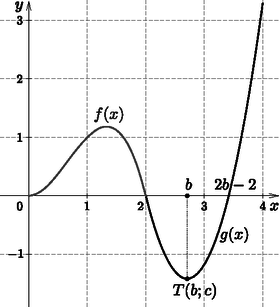Legyen $f\left(x\right)=2x^2-x^3$; $x\in \left[0;2\right]$. Az $f\left(x\right)$ függvény grafikonjához illesztettünk jobbról egy $y$ tengellyel párhuzamos tengelyű parabolát, amelyre az alábbiak egyszerre teljesülnek: $a)$ a két görbe törésmentesen csatlakozik egymáshoz a $2$ abszcisszájú pontban; $b)$ a parabola és az $x$ tengely által közrefogott síkidom területe egyenlő az $f\left(x\right)$ grafikonja és az $x$ tengely által bezárt síkidom területével. Adjuk meg a parabola egyenletét. (16 pont)   Megoldás. A parabola vehető a