Cím:	Gyakorló feladatsor emelt szintű matematika érettségire
Szerző(k):	Bíró Bálint, Eger
Füzet:	2020/november, 459 - 463. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Mely $x$ valós számokra értelmezhető az $\begin{array}{c}{\displaystyle f\left(x\right)=\sqrt[]{\frac{1-\sqrt[]{x-3}}{\text{log}{}_2\left(x-2\right)}}}\end{array}$ függvény? (5 pont) $b)$ Adjunk meg legalább két olyan valós számot, amelyekkel a $\begin{array}{c}{\displaystyle \sqrt[]{x-2}+\sqrt[]{2x+3}=\sqrt[]{3x+7}}\end{array}$ és a $\begin{array}{c}{\displaystyle {16}^x\cdot 8^{2x}\cdot 4^{6x}\cdot \sqrt[]{2}=64}\end{array}$ egyenletek valós gyökei valamilyen sorrendben egy-egy számtani sorozat egymás utáni tagjai lehetnek. (6 pont)     2. Az Agatha Christie műveiből készült Poirot-novellák című tv-sorozat ,,A csokoládésdoboz'' című epizódjának egyik jelenetében két szereplő, egy férfi és egy nő, egy operaelőadás hallgatása közben egy doboz belga csokoládét kóstolgatott. A dobozt a jelenet kezdetén bontották fel, és a dobozban kezdetben 7-féle csokoládéfigura volt, mindegyikből 4 darab az ábra szerint.     A női szereplő kedvence a korona alakú csokoládé. Kóstolgatás közben az udvariasság szabályai szerint mindig a hölgy választ először, aztán a férfi, majd újra a hölgy, aztán a férfi és így tovább. A férfi tudja, hogy a hölgy kedvence a koronás csokoládé, ezért ő sosem választ magának ilyet. Ezek figyelembevételével először elfogyasztanak 7 csokoládét, mindegyik fajtából egyet-egyet, mégpedig úgy, hogy a hölgy először a kedvencéből választ. $a)$ Hányféle sorrendben fogyaszthatnák el a 7 csokoládét? (6 pont) $b)$ Ha a megmaradt 21 csokoládéból a hölgy egyesével, véletlenszerűen és visszatevés nélkül kiválasztana 6 darabot, akkor mennyi lenne a valószínűsége, hogy azok között legalább 2 koronás csokoládét talál? (6 pont)   3. Anna és Boglárka unokatestvérek, az egyik megyeszékhely különböző iskoláiba járnak. Anna kilenc évvel idősebb Boglárkánál. Jelöljük Anna jelenlegi életkorát $A$-val, Boglárka jelenlegi életkorát $B$-vel ($A$ és $B$ pozitív egész számok). $a)$ Lehetséges-e, hogy $n$ ($n$ pozitív egész) év múlva Anna éppen háromszor olyan idős lesz, mint Boglárka? Hány év múlva fordulhat elő, hogy Anna kétszer olyan idős lesz, mint Boglárka? (Válaszunkat indokoljuk.) (4 pont) Anna és Boglárka is nagyon ügyesek matematikából. Órai teljesítményük, eddigi versenyeredményeik alapján a tanáraik benevezték őket egy matematikaversenyre. Anna matematika szakkörön is készül a versenyre. A szakkörre 21 tanuló jár, 9 lány és 12 fiú. A csoport diákjai mindannyian jó képességűek. A tanáruk úgy szeretné összeállítani a versenyre utazó 14 fős csapatot, hogy azon belül a nemek aránya azonos legyen a szakkörön belüli arányukkal. $b)$ Hányféleképpen állíthatja össze a versenyre utazó csapatot Anna szakkörének tanára? (3 pont) Anna a matematika területein belül legjobban a geometriát szereti. Egyszer rajzolt Boglárkának egy derékszögű trapézt és elmagyarázta unokatestvérének a trapéz tulajdonságait. Anna rajza az $ABCD$ trapéz, amelyben a $DA$ szár merőleges az $AB$ alapra. $c)$ Lehetséges-e, hogy a $CD$, $DA$, $AB$, $BC$ szakaszok hossza ebben a sorrendben egy mértani sorozat négy szomszédos tagja? (Válaszunkat indokoljuk.) 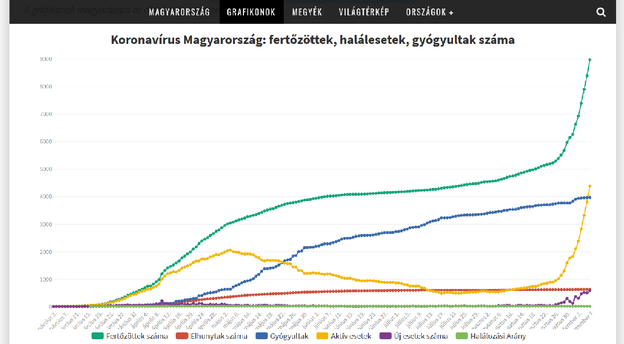(7 pont)   4. A koronavírus 2020. évi elterjedésével kapcsolatos adatokat a grafikonon szemlélhetjük (forrás: pandemia.hu).     A grafikon egyes adatait táblázatba foglaltuk márciustól szeptemberig minden hónap 6-án.   ${\displaystyle \begin{array}{|cc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">Fertőzöttek száma</span>}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">03.06.</span>}}\hfill & \hfill {\displaystyle \text{4}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">04.06.</span>}}\hfill & \hfill {\displaystyle \text{744}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">05.06.</span>}}\hfill & \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">06.06.</span>}}\hfill & \hfill {\displaystyle \text{3990}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">07.06.</span>}}\hfill & \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">08.06.</span>}}\hfill & \hfill {\displaystyle \text{4597}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">09.06.</span>}}\hfill & \hfill {\displaystyle \text{8387}}\hfill \\ \hline\end{array}}$   A következő táblázatban két tizedesjegyre kerekítve feltüntettük a magyarországi fertőzöttek számának napi átlagos növekedését az egyes időpontok között eltelt idő alatt (a megjelölt időpontok között eltelt napok számát megállapodás szerint úgy számítjuk, hogy az időintervallum felső időpontjának napját hozzászámítjuk az intervallumhoz, az alsó értéket nem).   ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{03.06.‐04.06.}}\hfill & \hfill {\displaystyle \text{04.06.‐05.06.}}\hfill & \hfill {\displaystyle \text{05.06.‐06.06.}}\hfill & \hfill {\displaystyle \text{06.06.‐07.06.}}\hfill & \hfill {\displaystyle \text{07.06.‐08.06.}}\hfill & \hfill {\displaystyle \text{08.06.‐09.06.}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{78,9}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{6,63}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill \\ \hline\end{array}}$   $a)$ Töltsük ki mindkét táblázat hiányzó részeit (egy-egy napon a fertőzöttek száma csak pozitív egész szám lehet, ezért a számítások során a kerekítés szabályainak megfelelően járjunk el). (4 pont) $b)$ Egy $n$ pontú teljes gráf élei közül 21 élet törölve egy fagráfot kapunk. Határozzuk meg $n$ értékét. (5 pont) $c)$ Bizonyítsuk be, hogy a ${11}^n+{60}^n\le {61}^n$ egyenlőtlenség $n=1$ kivételével minden pozitív egész számra teljesül. (5 pont)   II. rész     5. $a)$ Bizonyítsuk be, hogy a $2014\cdot 2016\cdot 2024\cdot 2026+100$ négyzetszám és állapítsuk meg, hogy melyik pozitív egész számnak a négyzete. (4 pont) $b)$ Igazoljuk, hogy a $\left]11\mathrm{,}5;\infty \right[$ számhalmazon értelmezett $\begin{array}{c}{\displaystyle f\left(x\right)=\sqrt[]{2x+28+10\cdot \sqrt[]{2x+3}}-\sqrt[]{2x+28-10\cdot \sqrt[]{2x+3}}}\end{array}$ függvény értéke állandó. Határozzuk meg ezt az állandó értéket. (5 pont) $c)$ Hány valós megoldása van a $\begin{array}{c}{\displaystyle \text{sin}{}^{4}x+\text{cos}{}^{4}x-\frac{5}{2}\cdot \text{sin}x\cdot \text{cos}x=\frac{1}{4}}\end{array}$ egyenletnek a $]-\frac{3\pi }{4};\frac{5\pi }{4}]$ számhalmazon? Adjuk meg a feltételeknek megfelelő összes megoldást. (7 pont)   6. Az $AB$ szakasz felezőpontja $O$, az $A$ ponthoz közelebbi negyedelőpontja $C$, a $B$ ponthoz közelebbi negyedelőpontja $D$. A $C$, $O$, $D$ pontokban az $AB$ szakaszra rajzolt merőlegesek az $AB$ átmérőjű félkört rendre a $P$, $Q$, $R$ pontokban metszik. $a)$ Határozzuk meg a $BQP$ és $BRQ$ háromszögek szögeit. (8 pont) $b)$ Hány százaléka a $BRQP$ négyszög területe az $ABP$ háromszög területének? (Az eredményt két tizedesjegyre kerekítve adjuk meg.) (8 pont)   7. Hány olyan $p$ pozitív prímszám van, amelyre nem igaz, hogy a $\begin{array}{c}{\displaystyle \left(p-2\right)\cdot x^2+\left(2p+3\right)\cdot x+p^2-1=0}\end{array}$ egyenletnek legfeljebb egy valós gyöke van? (16 pont)   8. Egy kocka minden élének hossza $n$, ahol $n$ pozitív egész szám. A kocka minden lapját fehérre festjük, majd a kockát a lapjaival párhuzamos síkok mentén $n^3$ darab egységnyi élű kockára daraboljuk. $a)$ Hányszorosa a kis kockák felszínének összege az eredeti kocka felszínének? (2 pont) Ezután az összes kis kocka lapjait megszámozzuk a következő szabály szerint: először azoknak a kis kockáknak a 6-6 lapját számozzuk meg a pozitív egész számokkal 1-től kiindulva, amelyeknek egyetlen lapja sem fehér, ezután a számozást folytatjuk azon kis kockák lapjaival, amelynek egy oldala fehér, utána a két fehér lappal rendelkező kis kockák következnek, végül azok a kis kockák, amelyeknek három lapja fehér. Ezzel az eljárással elérjük, hogy minden kis kocka minden lapján szerepel egy-egy pozitív egész szám és ezek a számok mind különbözők. $b)$ Legalább mekkora az $n$ szám, ha biztosan tudjuk, hogy a 2020 szám olyan kis kockára kerül, amelynek nincs fehérre festett lapja? (4 pont) $c)$ Határozzuk meg a pozitív egész $n$ számot, ha a fenti számozással a 4326 szám az utolsó olyan kis kocka utoljára megszámozott egyik lapjára kerül, amelynek pontosan két lapja fehér. (6 pont) $d)$ Az $n^3$ számú kis kockából véletlenszerűen kiválasztunk egy darabot. Mennyi annak az esélye, hogy a kiválasztott kis kockának legalább az egyik lapja fehér, ha $n=8$? (4 pont)   9. Az $ABC$ háromszög csúcsainak koordinátái a derékszögű koordináta-rendszerben $A\left(0;-2\right)$, $B\left(6;10\right)$, $C\left(-3;1\right)$. $a)$ Bizonyítsuk be, hogy az $ABC$ derékszögű háromszög. (3 pont) $b)$ Igazoljuk, hogy az $y=-x^2+8x-10$ egyenletű parabolának a $BC$ oldal egyenesével nincs közös pontja, de az $AB$ oldal egyenesével két közös pontja is van. Határozzuk meg az $AB$ oldal egyenese és az $y=-x^2+8x-10$ egyenletű parabola metszéspontjainak koordinátáit. (5 pont) $c)$ Számítsuk ki, hogy az $ABC$ háromszög területének hányadrészét fedik le azok a pontok, amelyekre $y\le -x^2+8x-10$ teljesül. (8 pont)