Cím:	Megoldásvázlatok a 2020/9. szám emelt szintű matematika gyakorló feladatsorához
Szerző(k):	Balga Attila ,  Székely Péter
Füzet:	2020/október, 397 - 409. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Adott két függvény: $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{2x+9}{3};g\left(x\right)=\sqrt[]{x^2+4x+4}\mathrm{.}}\end{array}$ Van-e olyan $x\in \text{R}$, ahol a két függvény helyettesítési értéke megegyezik? (6 pont) $b)$ Van-e olyan $p$ valós szám, amelyre az alábbi két kifejezés értéke egyenlő: $\begin{array}{c}{\displaystyle A=\text{log}{}_2\left(p+2\right)+\text{log}{}_2\left(p-2\right);B=1+\text{log}{}_2\left(p+10\right)?}\end{array}$ (6 pont)   Megoldás. $a)$ 1. megoldás. $g\left(x\right)={\sqrt[]{\left(x+2\right)}}^2=|x+2|$, $\begin{array}{c}{\displaystyle 2x+9=3\cdot |x+2|\mathrm{.}}\end{array}$ Ha $x<-2$, akkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2x+9}& {\displaystyle =-3x-\mathrm{6,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =-3.}\hfill \end{array}}$ Ha $x\ge -2$, akkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2x+9}& {\displaystyle =3x+\mathrm{6,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =3.}\hfill \end{array}}$ Ellenőrzés behelyettesítéssel vagy az ekvivalenciára való jogos hivatkozással. 2. megoldás. $2x+9=3\sqrt[]{x^2+4x+4}$, ha $x\ge \frac{-9}{2}$, akkor négyzetre emelhetünk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 4x^2+36x+81}& {\displaystyle =9x^2+36x+\mathrm{36,}}\hfill \\ \hfill {\displaystyle 9}& {\displaystyle =x^2\mathrm{,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =\pm 3.}\hfill \end{array}}$ Ellenőrzés behelyettesítéssel vagy az ekvivalenciára való jogos hivatkozással. $b)$ $\begin{array}{c}{\displaystyle \text{log}{}_2\left(p+2\right)+\text{log}{}_2\left(p-2\right)=1+\text{log}{}_2\left(p+10\right)\mathrm{.}}\end{array}$ Kikötés: $p>2$, $\begin{array}{c}{\displaystyle \text{log}{}_2\left(p^2-4\right)=\text{log}{}_2\left(2p+20\right)\mathrm{.}}\end{array}$ Mivel a $\text{log}{}_{2}x$ függvény szigorúan monoton: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle p^2-4}& {\displaystyle =2p+20}\hfill \\ \hfill {\displaystyle p^2-2p-24}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle p_1=-4;}& {\displaystyle p_2=6.}\hfill \end{array}}$ Csak a $p=6$ megoldás tesz eleget a feltételeknek. Az alaphalmazon ekvivalens átalakításokat végeztünk.   2. Solymász tanár úr biológia órájára $26$ végzős jár, és valamennyien részt vesznek imádott biológia tanáruk humánetológia óráján is. Félévkor a tanár úr (nevelő célzattal) meglehetősen szigorú volt, ezért $21$-en nem kaptak ötöst biológiából és $19$-en nem kaptak ötöst humánetológiából. Ugyanakkor $8$-an kaptak ötöst legalább az egyik tárgyból. $a)$ Hány végzős kapott ötöst mindkét tárgyból? (4 pont) A biológia próbaérettségit mind a $26$ diák megírta. A tanár úr korábbi szigorúsága elérte célját, mert a próbaérettségi már sokkal jobban sikerült. Senki sem kapott elégtelen, vagy elégséges osztályzatot. A közepes, jó és jeles osztályzatok száma ebben a sorrendben egy mértani sorozat három egymást követő eleme lett. A csoport átlaga $\frac{60}{13}$ lett. $b)$ Számoljuk ki a próbaérettségi osztályzatainak szórását. Az eredményt két tizedesjegy pontossággal adjuk meg. (8 pont)   Megoldás. $a)$ 1. megoldás. 5 tanulónak van ötöse biológiából, 7 tanulónak van ötöse humánetológiából; $5+7=12$, de csak 8 tanulónak van legalább az egyik tárgyból ötöse, ezért mindkét tárgyból 4 tanulónak van ötöse. 2. megoldás. Ha mindkét tárgyból $x$ tanulónak van ötöse, akkor csak biológiából $5-x$ tanulónak van ötöse. Csak humánetológiából $7-x$ tanulónak van ötöse. $\begin{array}{c}{\displaystyle 5-x+x+7-x=8.}\end{array}$ Tehát mindkét tárgyból 4 tanulónak van ötöse. $b)$ 1. megoldás. A hármas, négyes és ötös osztályzatok száma: $a$, $a\cdot q$, $a\cdot q^2$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a+aq+a{q}^2}& {\displaystyle =\mathrm{26,}}\hfill \\ \hfill {\displaystyle \frac{3a+4aq+5a{q}^2}{26}}& {\displaystyle =\frac{60}{13}\mathrm{.}}\hfill \end{array}}$ Mindkét egyenletből $a$-t kifejezve: $\begin{array}{c}{\displaystyle \frac{26}{1+q+q^2}=\frac{120}{3+4q+5q^2}\mathrm{.}}\end{array}$ Rendezés után: $\begin{array}{c}{\displaystyle 5q^2-8q-21=\mathrm{0,}{q}_1=-\frac{7}{5};q_2=3.}\end{array}$ Csak a $q=3$ felel meg a feladat feltételeinek, tehát 2 db hármas, 6 darab négyes és 18 darab ötös osztályzat született. Az osztályzatok szórása: $0\mathrm{,}6249\approx 0\mathrm{,}62$. 2. megoldás. Legyen a hármasok száma $a$, a négyesek száma $b$, az ötösök száma $c$. Ekkor az alábbi egyenleteket kapjuk: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle a+b+c}& {\displaystyle =\mathrm{26,}}\hfill & \text{(<mi>I</mi><mn>.</mn>)}\\ \hfill {\displaystyle \frac{3a+4b+5c}{26}}& {\displaystyle =\frac{60}{13}\mathrm{,}}\hfill & \text{(<mi>I</mi><mi>I</mi><mn>.</mn>)}\\ \hfill {\displaystyle b^2}& {\displaystyle =ac\mathrm{.}}\hfill & \text{(<mi>I</mi><mi>I</mi><mi>I</mi><mn>.</mn>)}\end{array}}$ Az első egyenletből: $a=26-b-c$. A második egyenletet átalakítva: $3a+4b+5c=120$. Az előző összefüggést beírva: $3\left(26-b-c\right)+4b+5c=120$. Ebből: $b=42-2c$ és $a=c-16$. Így a harmadik egyenlet: ${\left(42-2c\right)}^2=\left(c-16\right)\cdot c$. Az egyenletet rendezve: $3c^2-152c+1764=0$, ennek megoldásai: $c_1=18$ és $c_2=\frac{98}{3}$. Csak a $c=18$ felel meg a feladat feltételeinek, tehát 2 db hármas, 6 darab négyes és 18 darab ötös osztályzat született. Az osztályzatok szórása: $0\mathrm{,}6249\approx 0\mathrm{,}62$.   3. $a)$ Határozzuk meg az $f:\text{R}\to \text{R}$, $f\left(x\right)=x^3-3x^2-24x+2$ függvény lokális maximumhelyét. (5 pont) $b)$ Mekkora területet zár be a $g:\text{R}\to \text{R}$, $g\left(x\right)=3x^2-6x-24$ függvény grafikonja és az $x$ tengely? (6 pont) $c)$ Mennyi az $a_n=\frac{11n-5}{3n+8}$ sorozat határértéke? (3 pont)   Megoldás. $a)$ A deriváltfüggvény: $f\text{'}\left(x\right)=3x^2-6x-24$. A függvénynek ott lehet lokális szélsőértéke, ahol a derivált nulla. ${\displaystyle \begin{array}{c}\hfill {\displaystyle 3x^2-6x-24=\mathrm{0,}{x}_1=-2;x_2=4.}\hfill \\ \hfill {\displaystyle {\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mn>2</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mn>2</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2</mn><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo><mn>4</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mn>4</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>4</mn><mo stretchy="false"><</mo><mi>x</mi></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mo stretchy="false">'</mo><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↑</mo></math>}}\hfill & \hfill {\displaystyle \text{lok. max. h.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↓</mo></math>}}\hfill & \hfill {\displaystyle \text{lok. min. h.}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↑</mo></math>}}\hfill \\ \hline\end{array}}}\hfill \end{array}}$ Vagy a táblázat helyett: A második derivált, $f\text{'}\text{'}\left(x\right)=6x-6$, $f\text{'}\text{'}\left(-2\right)=-18<0$ és $f\text{'}\text{'}\left(4\right)=18>0$. Tehát a függvénynek az $x=-2$ helyen van lokális maximuma. $b)$ ${\displaystyle \begin{array}{c}\hfill {\displaystyle 3x^2-6x-24=\mathrm{0,}{x}_1=-2;x_2=\mathrm{4,}}\hfill \\ \hfill {\displaystyle T=|\underset{-2}{\overset{4}{\int }}\left(3x^2-6x-24\right)\text{d}x|=|{\left[x^3-3x^2-24x\right]}_{-2}^4|=}\hfill \\ \hfill {\displaystyle =|\left(64-48-96\right)-\left(-8-12+48\right)|=108.}\hfill \end{array}}$ $c)$ $\begin{array}{c}{\displaystyle \underset{n\to \infty }{\overset{}{\text{lim}}}\left(\frac{11n-5}{3n+8}\right)=\underset{n\to \infty }{\overset{}{\text{lim}}}\frac{11-\frac{5}{n}}{3+\frac{8}{n}}=\frac{11-0}{3+0}=\frac{11}{3}\mathrm{.}}\end{array}$   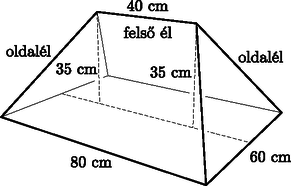4. Peti bá' egy téglalap alapú babaházat készített a lányainak. A téglalap oldalai 60 cm és 80 cm. A babaházra egy levehető ,,sátortetőt'' készített. A tető felső éle 40 cm hosszú, és a babaház téglalap alakú mennyezetének hosszabbik középvonala felett, attól 35 cm távolságra van. A tető oldalélei egyenlő hosszúak. $a)$ Számítsuk ki az oldalélek hosszát és a vízszintes síkkal bezárt szögüket. (7 pont)     Zsófi a tető trapéz alakú részére egy téglalap alakú díszt szeretne felragasztani. A téglalap egyik oldala illeszkedik a trapéz alapvonalára, két csúcsa pedig a trapéz száraira. $b)$ Mekkora a legnagyobb területű téglalap területe, amelyet a megadott módon el lehet helyezni a tetőn? A választ négyzetcentiméterben, egész számra kerekítve adjuk meg. (6 pont)   Megoldás. $a)$ (Az 4.a. ábra jelölései alapján.) Az oldalél hosszának kiszámítása: 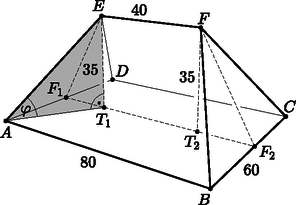    4.a. ábra   1. lehetőség. Az $A{T}_1{F}_1$ derékszögű háromszögben $F_1{T}_1=20$ és $A{F}_1=30$. A Pitagorasz-tétel az $A{F}_1{T}_1$ derékszögű háromszögben: $A{T}_1=\sqrt[]{{20}^2+{30}^2}=10\sqrt[]{13}\approx 36\mathrm{,}06$. Pitagorasz-tétel az $A{T}_{1}E$ derékszögű háromszögben: $A{E}^2=A{T}_1^2+E{T}_1^2$. $\begin{array}{c}{\displaystyle AE=\sqrt[]{{35}^2+{\left(10\sqrt[]{13}\right)}^2}=\left(\sqrt[]{{30}^2+{\left(5\sqrt[]{65}\right)}^2}\right)=5\sqrt[]{101}\approx 50\mathrm{,}25\text{cm}}\end{array}$ az oldalél hossza. 2. lehetőség. Pitagorasz-tétel az $E{F}_1{T}_1$ derékszögű háromszögben: $E{F}_1=\sqrt[]{{20}^2+{35}^2}=5\sqrt[]{65}\approx 40\mathrm{,}31$. Pitagorasz-tétel az $A{F}_{1}E$ derékszögű háromszögben: $A{E}^2=A{F}_1^2+E{F}_1^2$. $\begin{array}{c}{\displaystyle AE=\sqrt[]{{35}^2+{\left(10\sqrt[]{13}\right)}^2}=\left(\sqrt[]{{30}^2+{\left(5\sqrt[]{65}\right)}^2}\right)=5\sqrt[]{101}\approx 50\mathrm{,}25\text{cm}}\end{array}$ az oldalél hossza. Az oldalél vízszintes síkkal bezárt szöge a 4.a. ábrán $\phi$-vel jelölt $EA{T}_1$ szög, amelyre $\text{sin}\phi =\frac{35}{5\sqrt[]{101}}\approx 0\mathrm{,}6965$, ahonnan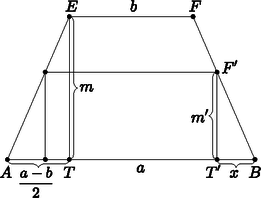: $\phi =44\mathrm{,}{15}^{\circ }$.     4.b. ábra   $b)$ A 4.b. ábra jelöléseit használva: $ATE▵\sim BT\text{'}F\text{'}▵$, mert szögeik egyenlők. $\begin{array}{c}{\displaystyle \frac{m\text{'}}{x}=\frac{2m}{a-b}\iff m\text{'}=\frac{2m}{a-b}\cdot x\mathrm{.}}\end{array}$ Ebből a téglalap területe: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T\left(x\right)}& {\displaystyle =\left(a-2x\right)\cdot \frac{2m}{a-b}\cdot x=\frac{2m}{a-b}\cdot \left(-{2x}^2+ax\right)=-\frac{4m}{a-b}\cdot \left(x^2-\frac{a}{2}\cdot x\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =-\frac{4m}{a-b}\cdot \left({\left(x-\frac{a}{4}\right)}^2-\frac{a^2}{16}\right)=-\frac{4m}{a-b}\cdot {\left(x-\frac{a}{4}\right)}^2+\frac{m{a}^2}{4\left(a-b\right)}\mathrm{.}}\hfill \end{array}}$ Tehát a terület maximális, ha $x=\frac{a}{4}=20$ cm.   II. rész     5. A DÖ $900$ pólót rendelt E5vös Napra. A pólókat két géppel nyomtatták. A gépeket kezdetben rosszul állították be, ezért az első gép (Horribile dictu!) a rajta nyomtatott $400$ póló $2\%$-ára tévesen, az E5vös helyett az Eötvös feliratot nyomtatta, és a másik gép ugyanezt a hibát követte el a rajta nyomtatott pólók 3,4%-ával. A minőségellenőrzéskor Bocó a $900$ alaposan összekevert pólóból véletlenszerűen kiválasztott egyet, és azon hibás volt a felirat. (Ezen persze kellőképpen elkeseredett $\text{...}$) $a)$ Mekkora annak a valószínűsége, hogy a hibás pólót a második gépen nyomtatták? (5 pont) A DÖ úgy döntött, hogy a hibásan nyomtatott póló árából először 500 Ft árengedményt ad, de a kereslet nagyon minimális volt, ezért az új árat még tovább kellett csökkenteni, annak $p\%$-ával. Így a póló 50 Ft-tal drágább lett, mintha először engedték volna le az árát $p\%$-kal és utána 500 Ft-tal, viszont 90 Ft-tal olcsóbb lett, mint ha mindkétszer az aktuális ár $p\%$-ával csökkentették volna az árát. $b)$ Mennyi volt a póló eredeti ára, és hány százalékos volt a csökkentés? (11 pont)   Megoldás. $a)$ 1. megoldás. Az első gépen 8, a második gépen 17 hibás pólót nyomtattak. Tehát 25 hibás póló van, ez az összes esetek száma. A kedvező esetek száma a második gépen készült pólók száma, azaz 17. Így a kérdéses valószínűség: $\frac{17}{25}=0\mathrm{,}68$. 2. megoldás. Az első gépen 8, a második gépen 17 hibás pólót nyomtattak. Legyen $A$ az az esemény, hogy a pólót a második gépen nyomtatták, $B$ pedig az az esemény, hogy a kiválasztott póló hibás. A keresett valószínűség: $p\left(A\mid B\right)=\frac{p\left(AB\right)}{p\left(B\right)}$. $\begin{array}{c}{\displaystyle p\left(AB\right)=\frac{17}{900}\mathrm{,}p\left(B\right)=\frac{25}{900}\mathrm{,}p\left(A\mid B\right)=\frac{\frac{17}{900}}{\frac{25}{900}}=\frac{17}{25}=0\mathrm{,}68.}\end{array}$ 3. megoldás. Annak valószínűsége, hogy egy póló az első gépen készült: $p\left(1.\right)=\frac{4}{9}$. Annak valószínűsége, hogy egy póló a második gépen készült: $p\left(2.\right)=\frac{5}{9}$. Annak valószínűsége, hogy egy póló hibás, ha az első gépen készült: $p\left(H\mid 1.\right)=0\mathrm{,}02$. Annak valószínűsége, hogy egy póló hibás, ha a második gépen készült: $p\left(H\mid 2.\right)=0\mathrm{,}034$. Bayes tétele alapján annak valószínűsége, hogy egy póló a második gépen készült, feltéve, hogy hibás: $\begin{array}{c}{\displaystyle p\left(2.\mid H\right)=\frac{p\left(H\mid 2.\right)\cdot p\left(2.\right)}{p\left(H\mid 1.\right)\cdot p\left(1\right)+p\left(H\mid 2.\right)\cdot p\left(2.\right)}\mathrm{.}}\end{array}$ Tehát a keresett valószínűség: $\begin{array}{c}{\displaystyle \frac{0\mathrm{,}034\cdot \frac{5}{9}}{0\mathrm{,}02\cdot \frac{4}{9}+0\mathrm{,}034\cdot \frac{5}{9}}=0\mathrm{,}68.}\end{array}$ $b)$ Legyen $x$ a póló árleszállítás előtti ára forintban, és legyen $q=1-\frac{p}{100}$. Ha a két árleszállítás fordított sorrendben történt volna, akkor a póló kétszeres árleszállítás utáni ára $xq-500$ forint, tehát $\begin{array}{c}{\displaystyle \left(xq-500\right)+50=\left(x-500\right)\cdot q\mathrm{.}}\end{array}$ Ha mindkét alkalommal $p\%$ a csökkentés, akkor az új ár $x{q}^2$ forint, tehát $\begin{array}{c}{\displaystyle \left(x-500\right)\cdot q+90=x{q}^2\mathrm{.}}\end{array}$ Az első egyenletből $q=0\mathrm{,}9$, azaz $p=10$. A $q$ értékét a második egyenletbe behelyettesítve: $\begin{array}{c}{\displaystyle \left(x-500\right)\cdot 0\mathrm{,}9+90=x\cdot 0\mathrm{,}\mathrm{81,}}\end{array}$ $x=4000$. A póló eredeti ára 4000 Ft, $p$ értéke pedig 10.   Ellenőrzés: $4000-500=3500$, $10\%$-kal csökkentve 3150; 4000 csökkentve 10%-kal 3600, $3600-500=3100$; 4000 csökkentve 10%-kal 3600, újabb 10%-kal csökkentve 3240. $3150=3100+50$ és $3150=3240-90$, tehát a kapott eredmények helyesek.   6. Fixi kerékpárunkon az első lánctányéron 46 fog található, a hátsó fogaskeréken pedig 18 fog van. (Az első lánctányérhoz rögzítik a pedált, a hátsó fogaskerék pedig a hátsó keréken van.)     1. ábra   Az 1. ábrán a lánc felülnézeti képe látható, a második ábrán pedig az, hogy miként illeszkedik a lánc a fogaskerékre. Két láncszem tengelye 1,27 cm távolságra van egymástól (lásd 2. ábra).     2. ábra   $a)$ Milyen hosszú lánc férne az első lánctányérra, ha teljesen körbetekernénk lánccal? 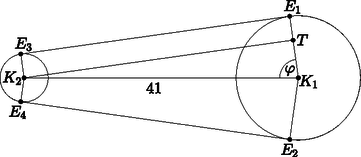(3 pont) A két fogaskerék (a pedál és a hátsó tengely) középpontja 41 cm van egymástól (3. ábra) és a lánc teljesen feszes. 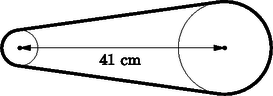    3. ábra   $b)$ Milyen hosszú lánc van a kerékpáron? (Válaszunkat centiméterben, két tizedesjegy pontossággal adjuk meg.) (10 pont) A láncokat gyártó üzemben 160 láncszemből álló láncdarabokat készítenek. A mérések alapján a láncdarabok 2%-ában egy szemmel kevesebb van, mint az előírás. A láncszemek számát egy számítógép ellenőrzi egy futószalagon. A futószalag különböző pontjain véletlenszerűen kiválaszt egy láncdarabot és meghatározza, hány láncszemből áll, de a futószalag folyamatosan mozog, ezért nem lehet kiemelni a hibás láncdarabot. Ennek megfelelően akár az az extrém eset is előfordulhat, hogy ugyanazt a láncdarabot ellenőrzi csak, akár többször is. Egy félórás időintervallumban 5000 láncdarab kering a futószalagon. $c)$ Határozzuk meg a fél óra alatt hibásnak talált láncdarabok várható értékét. (3 pont)   Megoldás. $a)$ Az első lánctányérra annyi láncszem fér, ahány fog található rajta, tehát 46. Így a lánctányérra tekert lánc hossza $46\cdot 1\mathrm{,}27=58\mathrm{,}42$ cm. $b)$ A lánc az ábrának megfelelően két kör közös külső érintőszakaszaiból és két körívből áll. Az első kör kerülete az előbbiek alapján 58,42 cm, így a kör sugara: $r_1=9\mathrm{,}298$ cm. A hátsó fogaskeréken 18 fog van, így a kerülete: $18\cdot 1\mathrm{,}27=22\mathrm{,}86$. A kör sugara: $r_2=3\mathrm{,}638$ cm.     Az ábra jelöléseit használva: $K_{2}T$ párhuzamos $E_3{E}_1$-gyel. Ekkor $K_{1}T=r_1-r_2=5\mathrm{,}66$. Az érintő merőleges az érintési pontba húzott sugárra, tehát a $K_2{K}_{1}T$ háromszög derékszögű. Felírva Pitagorasz tételét: $\begin{array}{c}{\displaystyle E_3{E}_1=K_{2}T=\sqrt[]{K_2{K}_1^2-{\left(r_1-r_2\right)}^2}=\sqrt[]{{41}^2-5\mathrm{,}{66}^2}=40\mathrm{,}61\text{cm.}}\end{array}$ Ugyanebben a háromszögben: $\text{cos}\phi =\frac{5\mathrm{,}66}{41}\approx 0\mathrm{,}138$, ebből $\phi =82\mathrm{,}{065}^{\circ }$. Az első lánctányéron lévő ív hossza: $\begin{array}{c}{\displaystyle i_1=\frac{{360}^{\circ }-2\phi }{{180}^{\circ }}\cdot r_1\cdot \pi \approx 31\mathrm{,}786\text{cm.}}\end{array}$ A hátsó fogaskeréken lévő ív hossza: $\begin{array}{c}{\displaystyle i_2=\frac{2\phi }{{180}^{\circ }}\cdot r_2\cdot \pi \approx 10\mathrm{,}421\text{cm.}}\end{array}$ Tehát a lánc hossza: 123,43 cm. $c)$ A hibás láncdarabok binomiális eloszlású valószínűségi változót alkotnak, melynek paraméterei $n=5000$ és $p=0\mathrm{,}02$. Így a várható érték: $n\cdot p=5000\cdot 0\mathrm{,}02=100$.   7. Ábel elkésett a matematika óráról. Amikor tanára kérdőre vonta, a következőképpen mentegetőzött: ,,Tanár úr! Fáj a lábam, ezért nem tudtam lépcsőn feljönni a harmadik emeletre. Lifttel kellett jönnöm, de a liftre ki van írva, hogy $13$ fő használhatja, és sokáig tartott, amíg összejött a $13$ ember.'' (Ezzel persze kitűnő lehetőséget biztosított matematika tanárának, hogy elmagyarázza a ,,legfeljebb'' és ,,legalább'' szavak matematikai lényegét $\text{...}$) Az E5vös Napokon az Igazgató Úr úgy döntött, hogy a tizenkettedikesek szabadon használhatják a liftet. A végzősök úgy gondolták, hogy ezt a lehetőséget maximálisan kihasználják, ezért minden esetben $13$-an szálltak be az üres liftbe. $a)$ Bizonyítsuk be, hogy minden ilyen alkalommal biztosan utazott a liftben legalább három olyan diák, akik osztálytársak voltak. (Az iskolában hat végzős osztály van.) (3 pont) Az E5vös Napokon a Ki Mit Tud?-ra $12$ fős diákzsűri is alakult, amelyet a végzős évfolyamból véletlenszerűen választottak ki. $b)$ Mekkora a valószínűsége annak, hogy minden osztályt pontosan két fő képviselt, ha az osztálylétszámok: $12$.A: $32$ fő, $12$.B: $33$ fő, $12$.C: $31$ fő, $12$.D: $30$ fő, $12$.E: $29$ fő, $12$.F: $28$ fő? (6 pont) A streetball döntője után a hat résztvevő kezet fogott egymással. Mivel a meccs kissé elfajult, ezért voltak, akik nem fogtak kezet. Flóra megkérdezte a résztvevőket, hogy hány emberrel fogtak kezet, és a következő válaszokat kapta: 5; 4; 3; 3; 2; 2. Flóra ezek után a következőt mondta: ,,Biztos, hogy van közöttetek legalább egy ember, aki nem tud számolni.'' $c)$ Mire alapozta állítását? (3 pont) Az E5vös Napok végén Főző úr, a technikus visszapakolta a kiadott eszközöket kis kuckójába. Lelkes segítői is akadtak, akik a kuckó elé odapakoltak két létrát, három fekete dobozt, négy projektort és öt vetítővásznat, meglehetősen nagy összevisszaságban. Főző úr, ezeket véletlenszerű sorrendben, egyesével bepakolta a helyére. $d)$ Hányféle módon történhetett ez, ha az azonos típusú eszközöket nem lehet megkülönböztetni egymástól? (4 pont)   Megoldás. $a)$ Alkalmazzuk a skatulya elvet, legyenek az osztályok a skatulyák. A liftben $6\cdot 2+1$ diák utazott. Így a skatulya elv általános alakja alapján van legalább egy olyan osztály, amelyből legalább három diák utazott a liftben. $b)$ A végzős évfolyamon összesen 183 diák van. Közülük választunk ki 12 diákot, így az összes esetek száma: $\left(\genfrac{}{}{0ex}{}{183}{12}\right)$. Az egyes osztályokból 2-2 főt rendre $\left(\genfrac{}{}{0ex}{}{32}{2}\right)$, $\left(\genfrac{}{}{0ex}{}{33}{2}\right)$, $\left(\genfrac{}{}{0ex}{}{31}{2}\right)$, $\left(\genfrac{}{}{0ex}{}{30}{2}\right)$, $\left(\genfrac{}{}{0ex}{}{29}{2}\right)$, $\left(\genfrac{}{}{0ex}{}{28}{2}\right)$ módon választhatjuk ki. Mivel ezeket egymástól függetlenül választhatjuk, ezért a kedvező esetek száma: $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{32}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{33}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{31}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{30}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{29}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{28}{2}\right)\mathrm{.}}\end{array}$ A keresett valószínűség: $\begin{array}{c}{\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{32}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{33}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{31}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{30}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{29}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{28}{2}\right)}{\left(\genfrac{}{}{0ex}{}{183}{12}\right)}=0\mathrm{,}00399\approx 0\mathrm{,}004.}\end{array}$ $c)$ Tekintsük a résztvevőket egy hatpontú egyszerű gráf csúcsainak. Két csúcs akkor van összekötve, ha a résztvevők kezet fogtak. Az egyes csúcsok fokszámainak összege: $5+4+3+3+2+2=19$. Mivel a csúcsok fokszámainak összege az élek számának kétszerese, így ez nem lehet páratlan szám. $d)$ A sorrendek száma az ismétléses permutáció segítségével számolható ki: $\begin{array}{c}{\displaystyle P_{14}^{\left\{2;3;4;5\right\}}=\frac{14!}{2!\cdot 3!\cdot 4!\cdot 5!}=2522520.}\end{array}$ Tehát 2 522 520-féle sorrendben pakolhatta be a dolgokat.   8. Ábrázoljuk derékszögű koordináta-rendszerben az alábbi ponthalmazokat: $a)$ $A:=\left\{P\left(x;y\right)\mid 9x^2-16y^2\ge 0\right\}$. (5 pont) $b)$ $B:=\left\{Q\left(x;y\right)\mid x^2+y^2\le 25\right\}$. (3 pont) $c)$ Mekkora az $A\cap B$ halmaz területe? (8 pont)   Megoldás. $a)$  $9x^2-16y^2=\left(3x-4y\right)\cdot \left(3x+4y\right)\ge 0$, $3x-4y\le 0$ és $3x+4y\le 0$, vagy $3x-4y\ge 0$ és $3x+4y\ge 0$ (4. ábra).     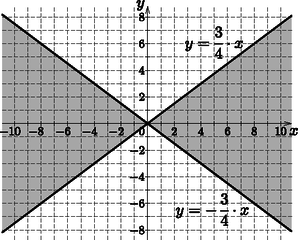4. ábra   $b)$ A keresett pontok az origó középpontú, 5 egység sugarú kör belseje és a körvonal (5. ábra). 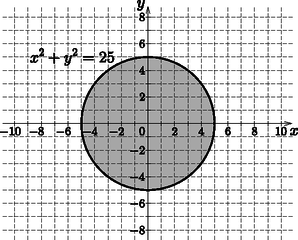    5. ábra   $c)$ A metszet két körcikk, amelyeket az egyenesek és az 5 egység sugarú kör határolnak (6. ábra). A körcikkekhez tartozó $\phi$ középponti szögre: $\begin{array}{c}{\displaystyle \text{tg}\frac{\phi }{2}=\frac{3}{4}\mathrm{,}\text{ ebből }=73\mathrm{,}{74}^{\circ }\mathrm{.}}\end{array}$ A metszet területe a két egybevágó körcikk területének összege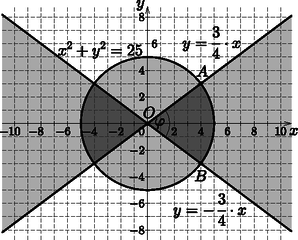: $\begin{array}{c}{\displaystyle T=2\cdot \frac{{73\mathrm{,}74}^{\circ }}{{360}^{\circ }}\cdot 5^2\pi =32\mathrm{,}18.}\end{array}$   6. ábra   A terület határozott integrál segítségével is kiszámítható. Az egyik körcikk felének területe: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{T}{2}=|{\int }_0^4\frac{3}{4}x\text{d}x|+|{\int }_4^5\sqrt[]{25-x^2}\text{d}x|\mathrm{,}}\hfill \\ \hfill {\displaystyle {\int }_0^4\frac{3}{4}x\text{d}x={\left[\frac{3}{8}{x}^2\right]}_0^4=\mathrm{6,}}\hfill \\ \hfill {\displaystyle {\int }_4^5\sqrt[]{25-x^2}\text{d}x={\int }_{\text{arcsin}\frac{4}{5}}^{\frac{\pi }{2}}\sqrt[]{25-25\text{sin}{}^{2}t}\cdot 5\text{cos}t\text{d}t={\int }_{\text{arcsin}\frac{4}{5}}^{\frac{\pi }{2}}25\text{cos}{}^{2}t\text{d}t=}\hfill \\ \hfill {\displaystyle =\frac{25}{2}\cdot {\int }_{\text{arcsin}\frac{4}{5}}^{\frac{\pi }{2}}\left(\text{cos}2t+1\right)\text{d}t=\frac{25}{2}\cdot {\left[\frac{1}{2}\text{sin}2t+t\right]}_{\text{arcsin}\frac{4}{5}}^{\frac{\pi }{2}}=}\hfill \\ \hfill {\displaystyle =\frac{25}{2}\left(\left(0+\frac{\pi }{2}\right)-\left(\frac{12}{25}+\text{arcsin}\frac{4}{5}\right)\right)=\frac{25}{4}\pi -6-\frac{25}{2}\text{arcsin}\frac{4}{5}\mathrm{.}}\hfill \end{array}}$ Tehát a keresett terület: $\begin{array}{c}{\displaystyle 2T=4\cdot \left(6+\frac{25}{4}\pi -6-\frac{25}{2}\text{arcsin}\frac{4}{5}\right)=25\pi -50\cdot \text{arcsin}\frac{4}{5}=32\mathrm{,}18.}\end{array}$   9. Egy piramisjáték elindítója az első héten öt embert szervezett be. A szervezés jól folytatódott, ezért a második héttől kezdődően a hetente beszervezettek száma a következő sorozat szerint alakult: $\begin{array}{c}{\displaystyle a_n=3\cdot a_{n-1}-8.}\end{array}$ $a)$ Összesen hányan vettek már részt az ötödik héten a játékban? (3 pont) $b)$ Igazoljuk, hogy a sorozat utolsó számjegyei periodikusan ismétlődő sorozatot alkotnak. (5 pont) $c)$ Bizonyítsuk be, hogy a sorozat $n$-edik eleme a másodiktól kezdve: $a_n=3^{n-1}+4$. (8 pont) Megoldás.  $a)$   $a_1$=5, $a_2$=3$\cdot$5-8=7, $a_3$=3$\cdot$7-8=13, $a_4$=3$\cdot$13-8=31, $a_5$=3$\cdot$31-8=85. Tehát az ötödik héten $5+7+13+31+85=141$ fő vett részt a játékban. $b)$ 1. megoldás. A sorozat elemeinek utolsó számjegyei az elemek 10-zel való osztási maradékai. Az osztási maradékokkal ugyanazt a műveletet kell végrehajtani, mint az eredeti számokkal. Az osztási maradékokból képzett $\left(b_n\right)$ sorozat elemei rendre: ${\displaystyle \begin{array}{cc}{\displaystyle }\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>b</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>5</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo>⋅</mo><mn>5</mn><mo stretchy="false">-</mo><mn>8</mn><mo stretchy="false">=</mo><mn>7</mn></math>, ennek 10-zel való osztási maradéka:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>b</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>7</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo>⋅</mo><mn>7</mn><mo stretchy="false">-</mo><mn>8</mn><mo stretchy="false">=</mo><mn>13</mn></math>, ennek 10-zel való osztási maradéka:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>b</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>3</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo>⋅</mo><mn>3</mn><mo stretchy="false">-</mo><mn>8</mn><mo stretchy="false">=</mo><mn>1</mn></math>, ennek 10-zel való osztási maradéka:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>b</mi></mrow><mrow><mn>4</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>1</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo>⋅</mo><mn>1</mn><mo stretchy="false">-</mo><mn>8</mn><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mn>5</mn></math>, ennek 10-zel való osztási maradéka:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>b</mi></mrow><mrow><mn>5</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>5</mn></math>. }}\hfill \end{array}}$ És ettől kezdve minden ismétlődik, hiszen ugyanazokkal a számokkal végezzük ugyanazokat a műveleteket. 2. megoldás. Használjuk fel a feladat $c)$ részében megadott $a_n=3^{n-1}+4$ képletet. Vizsgáljuk a három hatványainak 10-zel való osztási maradékait, ezekkel ugyanazokat a műveleteket kell végrehajtani, mint az eredeti számokkal: ${\displaystyle \begin{array}{cc}{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>3</mn></mrow><mrow><mn>0</mn></mrow></msup></mrow><mo stretchy="false">=</mo><mn>1</mn></math>, ennek 10-zel való osztási maradéka:}}\hfill & {\displaystyle \text{1,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>3</mn></mrow><mrow><mn>1</mn></mrow></msup></mrow><mo stretchy="false">=</mo><mn>3</mn><mo>⋅</mo><mrow><msup><mrow><mn>3</mn></mrow><mrow><mn>0</mn></mrow></msup></mrow></math>, ennek 10-zel való osztási maradéka:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo>⋅</mo><mn>1</mn><mo stretchy="false">=</mo><mn>3</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>3</mn></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">=</mo><mn>3</mn><mo>⋅</mo><mrow><msup><mrow><mn>3</mn></mrow><mrow><mn>1</mn></mrow></msup></mrow></math>, ennek 10-zel való osztási maradéka:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo>⋅</mo><mn>3</mn><mo stretchy="false">=</mo><mn>9</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>3</mn></mrow><mrow><mn>3</mn></mrow></msup></mrow><mo stretchy="false">=</mo><mn>3</mn><mo>⋅</mo><mrow><msup><mrow><mn>3</mn></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>, ennek 10-zel való osztási maradéka:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo>⋅</mo><mn>9</mn><mo stretchy="false">=</mo><mn>27</mn></math>, azaz 7,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>3</mn></mrow><mrow><mn>4</mn></mrow></msup></mrow><mo stretchy="false">=</mo><mn>3</mn><mo>⋅</mo><mrow><msup><mrow><mn>3</mn></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>, ennek 10-zel való osztási maradéka:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo>⋅</mo><mn>7</mn><mo stretchy="false">=</mo><mn>21</mn></math>, azaz 1. }}\hfill \end{array}}$ Ettől kezdve az osztási maradékokban ismétlődik az $1;3;9;7$ sorozat. Ekkor az eredeti sorozat utolsó számjegyei az $5;7;3;1$ ismétlődő sorozatot alkotják. $c)$ 1. megoldás. A bizonyítást teljes indukcióval végezzük: $a_1=5=3^0+4$, az állítás igaz. Tegyük fel, hogy $n=k$-ra igaz, hogy $a_k=3^{k-1}+4$. Állítás: $n=k+1$-ra igaz, hogy $a_{k+1}=3^k+4$. Bizonyítás: A rekurziós megadással: $a_{k+1}=3\cdot a_k-8$. Az indukciós feltételt felhasználva: $a_{k+1}=3\cdot \left(3^{k-1}+4\right)-8=3^k+4$. Beláttuk, hogy ha az állítás igaz a $k$ természetes számra, akkor a $k+1$ természetes számra is igaz. Mivel az állítás igaz az $n=1$-re, ezért minden természetes számra igaz. 2. megoldás. Írjuk fel a sorozat elemeit az első elem és a rekurziós képlet segítségével: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_1}& {\displaystyle =5=3^0+\mathrm{4,}}\hfill \\ \hfill {\displaystyle a_2}& {\displaystyle =3\cdot 5-\mathrm{8,}}\hfill \\ \hfill {\displaystyle a_3}& {\displaystyle =3\cdot \left(3\cdot 5-8\right)-8=3^2\cdot 5-3\cdot 8-8=3^2\cdot 5-\left(3+1\right)\cdot \mathrm{8,}}\hfill \\ \hfill {\displaystyle a_4}& {\displaystyle =3\cdot \left(3^2\cdot 5-3\cdot 8-8\right)-8=3^3\cdot 5-3^2\cdot 8-3\cdot 8-8=3^3\cdot 5-\left(3^2+3+1\right)\cdot 8.}\hfill \end{array}}$ Ezek alapján: $a_n=3^{n-1}\cdot 5-\left(3^{n-2}+3^{n-3}+\text{...}+1\right)\cdot 8$. A mértani sorozat összegképletével: $\begin{array}{c}{\displaystyle a_n=3^{n-1}\cdot 5-\frac{3^{n-1}-1}{3-1}\cdot 8=3^{n-1}\cdot 5-4\cdot 3^{n-1}+4=3^{n-1}+4.}\end{array}$  Balga Attila, Székely Péter  Budapest, V. kerületi Eötvös József Gimnázium